Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-05-02T11:28:15.443Z Has data issue: false hasContentIssue false
  • English
  • Français

Qualitative properties of solutions for system involving the fractional Laplacian

Part of: Elliptic equations and systems Partial differential equations Miscellaneous topics - Partial differential equations

Published online by Cambridge University Press:  26 February 2024

Ran Zhuo  and
Yingshu Lü
Ran Zhuo
Affiliation:
Department of Mathematics, Shanghai Normal University, Shanghai 200234, People's Republic of China (zhuoran1986@126.com)
Yingshu Lü
Affiliation:
Institute of Natural Sciences, CMA-Shanghai, Shanghai Jiao Tong University, Shanghai 200240, People's Republic of China (yingshulv@sjtu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we consider the following non-linear system involving the fractional Laplacian0.1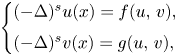

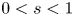\begin{equation} \left\{\begin{array}{@{}ll} (-\Delta)^{s} u (x)= f(u,\,v), \\ (-\Delta)^{s} v (x)= g(u,\,v), \end{array} \right. \end{equation}
in two different types of domains, one is bounded, and the other is an infinite cylinder, where $0< s<1$. We employ the direct sliding method for fractional Laplacian, different from the conventional extension and moving planes methods, to derive the monotonicity of solutions for (0.1) in $x_n$ 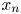variable. Meanwhile, we develop a new iteration method for systems in the proofs. Hopefully, the iteration method can also be applied to solve other problems.

Keywords

fractional Laplaciannarrow region principlesliding methodmonotonicity

MSC classification

Primary: 35B50: Maximum principles
Secondary: 35J60: Nonlinear elliptic equations 35R11: Fractional partial differential equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 16
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angenent, S. B.. Uniqueness of the solution of a semilinear boundary value problem. Math. Ann. 272 (1985), 129–138.CrossRefGoogle Scholar
Applebaum, D.. Lévy Processes and Stochastic Calculus. 2nd ed., Cambridge Studies in Advanced Mathematics, Vol. 116 (Cambridge University Press, Cambridge, 2009).CrossRefGoogle Scholar
Berestycki, H. and Nirenberg, L.. On the method of moving planes and the sliding method. Bol. Soc. Brasil Mat. (N.S.) 22 (1991), 1–37.CrossRefGoogle Scholar
Bertoin, J.. Lévy Processes. Cambridge Tracts in Mathematics, Vol. 121 (Cambridge University Press, Cambridge, 1996).Google Scholar
Bouchard, J. P. and Georges, A.. Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys. Rep. 195 (1990), 127–293.CrossRefGoogle Scholar
Berestycki, H., Caffarelli, L. and Nirenberg, L.. Monotonicity for elliptic equations in unbounded Lipschitz domains. Commum. Pure Appl. Math. 50 (1997), 1089–1111.3.0.CO;2-6>CrossRefGoogle Scholar
Cabré, X. and Tan, J.. Positive solutions of nonlinear problems involving the square root of the Laplacian. Adv. Math. 224 (2010), 2052–2093.CrossRefGoogle Scholar
Caffarelli, L. and Silvestre, L.. An extension problem related to the fractional Laplacian. Comm. Partial Differential Equations. 32 (2007), 1245–1260.CrossRefGoogle Scholar
Caffarelli, L. and Vasseur, A.. Drift diffusion equations with fractional diffusion and the quasi-geostrophic equation. Ann. Math. 171 (2010), 1903–1930.CrossRefGoogle Scholar
Chen, W., Fang, Y. and Yang, R.. Liouville theorems involving the fractional Laplacian on a half space. Adv. Math. 274 (2015), 167–198.CrossRefGoogle Scholar
Chen, W. and Li, C.. Classification of solutions of some nonlinear elliptic equations. Duke Math. J. 63 (1991), 615–622.CrossRefGoogle Scholar
Chen, W., Li, C. and Li, Y.. A direct method of moving planes for the fractional Laplacian. Adv. Math. 308 (2017), 404–437.CrossRefGoogle Scholar
Chen, W., Li, C. and Ou, B.. Classification of solutions for an integral equation. Comm. Pure Appl. Math. 59 (2006), 330–343.CrossRefGoogle Scholar
Chen, W. and Li, C., Methods on Nonlinear Elliptic Equations. AIMS Series on Differential Equations and Dynamical Systems, Vol. 4, (2010).Google Scholar
Clément, P. and Sweers, G.. Existence and multiplicity results for a semilinear elliptic eigenvalue problem. Ann. Scuola Norm. Sup. Pisa Cl. Sci. 14 (1987), 97–121.Google Scholar
Constantin, P.. Euler equations, Navier-Stokes equations and turbulence. Mathematical foundation of turbulent viscous flows, Lecture Notes in Math., Vol. 1871 (Springer, Berlin, 2006), pp. 1–43.Google Scholar
Dipierro, S., Soave, N. and Valdinoci, E.. On fractional elliptic equations in Lipschitz sets and epigraphs: regularity, monotonicity and rigidity results. Math. Ann. 369 (2017), 1283–1326.CrossRefGoogle Scholar
Gidas, B., Ni, W. and Nirenberg, L.. Symmetry and related properties via the maximum principle. Commun. Math. Phys. 68 (1979), 209–243.CrossRefGoogle Scholar
Mou, C.. Nonlinear elliptic systems involving the fractional Laplacian in the unit ball and on a half space. Commun. Pure Appl. Anal. 14 (2015), 2335–2362.CrossRefGoogle Scholar
Quaas, A. and Xia, A.. Liouville type theorems for nonlinear elliptic equations and systems involving fractional Laplacian in the half space. Calc. Var. Partial Differ. Equ. 52 (2015), 641–659.CrossRefGoogle Scholar
Silvestre, L.. Regularity of the obstacle problem for a fractional power of the Laplace operator. Commun. Pure Appl. Math. 60 (2007), 67–112.CrossRefGoogle Scholar
Tarasov, V. E. and Zaslasvky, G. M.. Fractional dynamics of systems with long-range interaction. Commun. Nonlinear Sci. Numer. Simul. 11 (2006), 885–889.CrossRefGoogle Scholar
Wu, L. and Chen, W.. Sliding methods for the fractional Laplacian. Adv. Math. 361 (2020), 106933.CrossRefGoogle Scholar
Wu, L. and Chen, W.. Monotonicity of solutions for fractional equations with De Giorgi type nonlinearities (in Chinese). Sci. Sin. Math. 50 (2020), 1–22.Google Scholar
Zhuo, R., Chen, W., Cui, X. and Yuan, Z.. Symmetry and non-existence of solutions for a nonlinear system involving the fractional Laplacian. Discrete Contin. Dyn. Syst. 36 (2016), 1125–1141.Google Scholar