Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-15T19:05:18.618Z Has data issue: false hasContentIssue false
  • English
  • Français

p-Summing operators on injective tensor products of spaces

Published online by Cambridge University Press:  14 November 2011

Stephen Montgomery-Smith  and
Paulette Saab
Stephen Montgomery-Smith
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO 65211, U.S.A.
Paulette Saab
Affiliation:
Department of Mathematics, University of Missouri, Columbia, MO 65211, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let X, Y and Z be Banach spaces, and let Πp (Y, Z) (1 ≦ p < ∞) denote the space of p-summing operators from Y to Z. We show that, if X is a ℒ∞-space, then a bounded linear operator 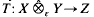is 1-summing if and only if a naturally associated operator T#: X → Πl (Y, Z) is 1-summing. This result need not be true if X is not a ℒ∞-space. For p > 1, several examples are given with X = C[0, 1] to show that T# can be p-summing without T being p-summing. Indeed, there is an operator T on 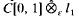whose associated operator T# is 2-summing, but for all N ∈ N, there exists an N-dimensional subspace U of 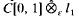such that T restricted to U is equivalent to the identity operator on 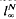. Finally, we show that there is a compact Hausdorff space K and a bounded linear operator 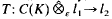for which T#: C(K) → Π1 (l1, l2) is not 2-summing.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 120 , Issue 3-4 , 1992 , pp. 283 - 296
Copyright
Copyright © Royal Society of Edinburgh 1992

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bilyeu, R. and Lewis, P.. Some mapping properties of representing measures. Ann. Math. Pure Appl. 109 (1976), 273–287.CrossRefGoogle Scholar
2Choquet, G.. Lectures on Analysis, Vol. II (New York: Benjamin, 1969).Google Scholar
3Diestel, J. and Uhl, J. J. Jr.Vector Measures, Math. Surveys 15 (Providence, R.I.: American Mathematical Society, 1977).CrossRefGoogle Scholar
4Figiel, T., Lindenstrauss, J. and Milman, V.. The dimension of almost spherical sections of convex bodies. Acta Math. 139 (1977), 53–94.CrossRefGoogle Scholar
5Grothendieck, A.. Produits tensoriels topologiques et espaces nucléaires. Mem. Amer. Math. Soc. 16 (1955).Google Scholar
6Hunt, R. A.. On L(p, q) spaces. Enseign. Math. (2) 12 (1966), 249–275.Google Scholar
7Jameson, G. J. O.. Summing and Nuclear Norms in Banach Space Theory, London Mathematical Society Student Texts (Cambridge: Cambridge University Press, 1987).CrossRefGoogle Scholar
8Jameson, G. J. O.. Relations between summing norms of mappings on l∞. Math. Z. 194 (1987), 89–94.CrossRefGoogle Scholar
9Kwapien, S.. On operators factorizable through L p-spaces. Bull. Soc. Math. France, Mém. 31–32 (1972), 215–225.CrossRefGoogle Scholar
10Pisier, G.. Factorization of Linear Operators and Geometry of Banach Spaces, AMS CBMS 60 (Providence, R.I.: American Mathematical Society, 1986).CrossRefGoogle Scholar
11Pisier, G.. Factorization of operators through L p∞ or L p1 and non commutative generalizations. Math. Ann. 276 (1986), 105–136.CrossRefGoogle Scholar
12Retherford, J. R. and Stegall, C.. Fully Nuclear and Completely Nuclear Operators with applications to ℒ1 and ℒ∞ spaces, Trans. Amer. Math. Soc. 163 (1972), 457–492.Google Scholar
13Saab, P.. Integral Operators on Spaces of Continuous Vector Valued Functions. Proc. Amer. Math. Soc. 111 (1991), 1003–1013.CrossRefGoogle Scholar
14Smith, B.. Some Bounded Linear Operators On the Spaces C(Ω, E) and A(K, E) (Ph.D. Dissertation, The University of Missouri-Columbia, 1989).Google Scholar
15Stegall, C.. Characterization of Banach spaces whose duals are L 1 spaces, Israel J. Math. 11 (1972), 299–308.CrossRefGoogle Scholar
16Swartz, C.. Absolutely summing and dominated operators on spaces of vector-valued continuous functions. Trans. Amer. Math. Soc. 179 (1973), 123–132.CrossRefGoogle Scholar