Hostname: page-component-848d4c4894-ttngx Total loading time: 0 Render date: 2024-06-07T01:58:20.527Z Has data issue: false hasContentIssue false
  • English
  • Français

On idempotent affine mappings

Published online by Cambridge University Press:  14 November 2011

R. J. H. Dawlings
R. J. H. Dawlings
Affiliation:
Bayero University, PMB 3011, Kano, Nigeria
Get access Rights & Permissions [Opens in a new window]

Synopsis

Let V be a vector space and End (V) the semigroup of endomorphisms of V. An affine mapping of V is a map A: V → V given by xA = xα + a, where a belongs to End (V) and a is some element of V. Let 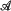(V) be the semigroup of affine mappings of V.

Let E' denote the non-injective idempotents of End (V) and let ℰ denote the idempotents of 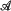(V). In this paper 〈ℰ〉 is determined in terms of 〈E′〉 when End (V) consists of all endomorphisms of V and when End (V) only contains the continuous endomorphisms (in which case we restrict V to being an inner product space).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 93 , Issue 3-4 , 1983 , pp. 345 - 348
Copyright
Copyright © Royal Society of Edinburgh 1983

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Dawlings, R. J. H.. Semigroups of Singular Endomorphisms of Vector Spaces (St Andrews Univ. Ph.D. Thesis, 1980).Google Scholar
2Dawlings, R. J. H.. The idempotent generated subsemigroup of the semigroup of continuous endomorphisms of a separable Hilbert space. Proc. Roy. Soc. Edinburgh Sect. A, to appear.Google Scholar
3Erdos, J. A.. On products of idempotent matrices. Glasgow Math. J. 8 (1967), 118–122.CrossRefGoogle Scholar