Hostname: page-component-848d4c4894-m9kch Total loading time: 0 Render date: 2024-04-30T16:04:20.227Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonlinear elasticity with vanishing nonlocal self-repulsion

Part of: Miscellaneous topics in calculus of variations and optimal control Equations of mathematical physics and other areas of application

Published online by Cambridge University Press:  28 September 2023

Stefan Krömer Open the ORCID record for Stefan Krömer [Opens in a new window]  and
Philipp Reiter Open the ORCID record for Philipp Reiter [Opens in a new window]
Stefan Krömer
Affiliation:
The Czech Academy of Sciences, Institute of Information Theory and Automation (ÚTIA), Pod vodárenskou věží 4, 182 08 Praha 8, Prague, Czech Republic (skroemer@utia.cas.cz)
Philipp Reiter
Affiliation:
Faculty of Mathematics, Chemnitz University of Technology, 09107 Chemnitz, Germany (reiter@math.tu-chemnitz.de)
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for nonlinear elastic energies with strong enough energetic control of the outer distortion of admissible deformations, almost everywhere global invertibility as constraint can be obtained in the $\Gamma$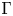-limit of the elastic energy with an added nonlocal self-repulsion term with asymptocially vanishing coefficient. The self-repulsion term considered here formally coincides with a Sobolev–Slobodeckiĭ seminorm of the inverse deformation. Variants near the boundary or on the surface of the domain are also studied.

Keywords

Nonlinear elasticitylocal injectivityglobal injectivityCiarlet–Nečas conditionnonlocal self-repulsionSobolev–Slobodeckiĭseminorm

MSC classification

Primary: 49N99: None of the above, but in this section
Secondary: 65Z05: Applications to physics 35Q74: PDEs in connection with mechanics of deformable solids
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 18
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aigerman, N. and Lipman, Y.. Injective and bounded distortion mappings in 3D. ACM Trans. Graph. 32 (2013), 106:1–106:14.CrossRefGoogle Scholar
Ball, J.. Global invertibility of Sobolev functions and the interpenetration of matter. Proc. R. Soc. Edinb. A. Math. 88 (1981), 315–328.CrossRefGoogle Scholar
Ball, J. M.. Convexity conditions and existence theorems in nonlinear elasticity. Arch. Ration. Mech. Anal. 63 (1976/77), 337–403.CrossRefGoogle Scholar
Ball, J. M. and Zarnescu, A.. Partial regularity and smooth topology-preserving approximations of rough domains. Calc. Var. Partial Differ. Equ. 56 (2017), 13.CrossRefGoogle Scholar
Bartels, S. and Reiter, Ph.. Numerical solution of a bending-torsion model for elastic rods. Numer. Math. 146 (2020), 661–697.CrossRefGoogle Scholar
Bartels, S. and Reiter, Ph.. Stability of a simple scheme for the approximation of elastic knots and self-avoiding inextensible curves. Math. Comput. 90 (2021), 1499–1526.CrossRefGoogle Scholar
Bartels, S., Reiter, Ph. and Riege, J.. A simple scheme for the approximation of self-avoiding inextensible curves. IMA J. Numer. Anal. 38 (2018), 543–565.CrossRefGoogle Scholar
Braides, A., $\Gamma$-convergence for beginners, Oxford Lecture Series in Mathematics and its Applications, Vol. 22 (Oxford University Press, Oxford, 2002).Google Scholar
Brezis, H.. How to recognize constant functions. A connection with Sobolev spaces. Uspekhi Mat. Nauk 57 (2002), 59–74.Google Scholar
Ciarlet, P. G., Mathematical elasticity. Vol. I, Studies in Mathematics and its Applications, Vol. 20 (North-Holland Publishing Co., Amsterdam, 1988. Three-dimensional elasticity).Google Scholar
Ciarlet, P. G. and Nečas, J.. Injectivity and self-contact in nonlinear elasticity. Arch. Ration. Mech. Anal. 97 (1987), 171–188.CrossRefGoogle Scholar
Elbau, P., Sequential lower semi-continuity of non-local functionals. Preprint arXiv:1104.2686 (2011).Google Scholar
Fonseca, I. and Gangbo, W., Degree theory in analysis and applications, Oxford Lecture Series in Mathematics and its Applications, Vol. 2 (The Clarendon Press, Oxford University Press, New York, 1995. Oxford Science Publications).Google Scholar
Foss, M., Hrusa, W. J. and Mizel, V. J.. The Lavrentiev gap phenomenon in nonlinear elasticity. Arch. Ration. Mech. Anal. 167 (2003), 337–365.CrossRefGoogle Scholar
Gonzalez, O. and Maddocks, J. H.. Global curvature, thickness, and the ideal shapes of knots. Proc. Natl. Acad. Sci. USA 96 (1999), 4769–4773.CrossRefGoogle ScholarPubMed
Grandi, D., Kružík, M., Mainini, E. and Stefanelli, U.. A phase-field approach to Eulerian interfacial energies. Arch. Ration. Mech. Anal. 234 (2019), 351–373.CrossRefGoogle Scholar
Henao, D., Mora-Corral, C. and Oliva, M.. Global invertibility of Sobolev maps. Adv. Calc. Var. 14 (2021), 207–230.CrossRefGoogle Scholar
Hencl, S. and Koskela, P., Lectures on mappings of finite distortion, Lecture Notes in Mathematics, Vol. 2096 (Springer, Cham, 2014).CrossRefGoogle Scholar
Hermes, T., Repulsive Potentiale in geometrischen Flüssen. Diploma thesis, RWTH Aachen University, 2008.Google Scholar
Krömer, S.. Global invertibility for orientation-preserving Sobolev maps via invertibility on or near the boundary. Arch. Ration. Mech. Anal. 238 (2020), 1113–1155.CrossRefGoogle Scholar
Krömer, S. and Valdman, J.. Global injectivity in second-gradient nonlinear elasticity and its approximation with penalty terms, Math. Mech. Solids 24 (2019), 3644–3673.CrossRefGoogle Scholar
Krömer, S. and Valdman, J.. Surface penalization of self-interpenetration in linear and nonlinear elasticity, Appl. Math. Model. 122 (2023), 641–664.CrossRefGoogle Scholar
Marcus, M. and Mizel, V. J.. Transformations by functions in Sobolev spaces and lower semicontinuity for parametric variational problems. Bull. Am. Math. Soc. 79 (1973), 790–795.CrossRefGoogle Scholar
Mielke, A. and Roubíček, T.. Rate-independent elastoplasticity at finite strains and its numerical approximation. Math. Models Methods Appl. Sci. 26 (2016), 2203–2236.CrossRefGoogle Scholar
O'Hara, J.. Energy of a knot. Topology 30 (1991), 241–247.CrossRefGoogle Scholar
Pedregal, P.. Weak lower semicontinuity and relaxation for a class of non-local functionals. Rev. Mat. Complut. 29 (2016), 485–495.CrossRefGoogle Scholar
Unseld, H. A., Numerik elastischer Kurven ohne Selbstdurchdringung. Staatsexamensarbeit supervised by Gerhard Dziuk, University of Freiburg i. Br., 2002.Google Scholar
Villamor, E. and Manfredi, J. J.. An extension of Reshetnyak's theorem. Indiana Univ. Math. J. 47 (1998), 1131–1145.CrossRefGoogle Scholar
Yu, C., Brakensiek, C., Schumacher, H. and Crane, K.. Repulsive surfaces. ACM Trans. Graph. 40 (2021).CrossRefGoogle Scholar