Hostname: page-component-84b7d79bbc-x5cpj Total loading time: 0 Render date: 2024-08-01T09:47:52.685Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple transition layers in a singularly perturbed differential-delay equation

Published online by Cambridge University Press:  14 November 2011

John Mallet-Paret  and
Roger D. Nussbaum
John Mallet-Paret
Affiliation:
Division of Applied Mathematics, Brown University, Providence, RI02912, U.S.A.
Roger D. Nussbaum
Affiliation:
Department of Mathematics, Rutgers University, New Brunswick, NJ 08903, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

The singularly perturbed differential-delay equation

is studied for a class of step-function nonlinearities f. We show that in general the discrete system

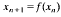
does not mirror the dynamics of (*), even for small ε, but that rather a different system

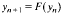
does. Here F is related to, but different from, f, and describes the evolution of transition layers. In this context, we also study the effects of smoothing out the discontinuities of f.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 123 , Issue 6 , 1993 , pp. 1119 - 1134
Copyright
Copyright © Royal Society of Edinburgh 1993

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Chow, S.-N., Lin, X.-B. and Mallet-Paret, J.. Transition layers for singularly perturbed delay differential equations with monotone nonlinearities. J. Dynamics Differential Equations 1 (1989), 3–43.CrossRefGoogle Scholar
2Chow, S.-N. and Mallet-Paret, J.. Singularly perturbed delay differential equations. In Coupled Nonlinear Oscillators, eds. Chandra, J. and Scott, A. C.. North Holland Math. Studies 80 (1983), 7–12.Google Scholar
3Crutchfield, J. P. and Huberman, B. A.. Fluctuations in the onset of chaos. Phys. Lett. A 77 (1980), 407–410.CrossRefGoogle Scholar
4Ivanov, A. F. and Sharkovsky, A. N.. Oscillations in singularly perturbed delay equations. Dynamics Reported 1 (1991), 164–224.CrossRefGoogle Scholar
5Li, T.-Y. and Yorke, J. A.. Period three implies chaos. Amer. Math. Monthly 82 (1975), 985–992.CrossRefGoogle Scholar
6Mallet-Paret, J. and Nussbaum, R. D.. Global continuation and complicated trajectories for periodic solutions of a differential-delay equation. Proc. Sympos. Pure Math. 45 (1986), 155–167.CrossRefGoogle Scholar
7Mallet-Paret, J. and Nussbaum, R. D.. Global continuation and asymptotic behaviour for periodic solutions of a differential-delay. Ann. Mat. Pura Appl. 145 (1986), 33–128.CrossRefGoogle Scholar
8Mallet-Paret, J. and Nussbaum, R. D.. A bifurcation gap for a singularly perturbed delay equation. In Chaotic Dynamics and Fractals, eds Barnsley, M. F. and Demko, S. G., 263–286. (New York: Academic Press; 1986).Google Scholar
9Sharkovskii, A. N.. Coexistence of cycles of a continuous map of the line into itself Ukr. Mat. Zhur. 16 (1964), 61–71 (in Russian).Google Scholar