Hostname: page-component-848d4c4894-cjp7w Total loading time: 0 Render date: 2024-07-02T17:16:54.988Z Has data issue: false hasContentIssue false
  • English
  • Français

Morse theory of Bestvina–Brady type for posets and matchings

Part of: Ordered sets PL-topology Applied homological algebra and category theory Homotopy theory

Published online by Cambridge University Press:  09 February 2023

Elías Gabriel Minian
Elías Gabriel Minian*
Affiliation:
Departamento de Matemática-IMAS, FCEyN, Universidad de Buenos Aires, Buenos Aires, Argentina (gminian@dm.uba.ar)
Get access Rights & Permissions [Opens in a new window]

Abstract

We introduce a Morse theory for posets of Bestvina–Brady type combining matchings and height functions. This theory generalizes Forman's discrete Morse theory for regular CW-complexes and extends previous results on Morse theory for $h$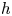-regular posets to all finite posets. We also develop a relative version of Morse theory which allows us to compare the topology of a poset with that of a given subposet.

Keywords

Morse theorysimplicial complexesfinite topological spacesposetsmatchings

MSC classification

Primary: 55U05: Abstract complexes
Secondary: 55P15: Classification of homotopy type 57Q05: General topology of complexes 06A06: Partial order, general
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 1 , February 2024 , pp. 209 - 220
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barmak, J. A.. Algebraic topology of finite topological spaces and applications. Lecture Notes in Mathematics, vol. 2032 (Heidelberg: Springer, 2011).CrossRefGoogle Scholar
Barmak, J. A. and Minian, E. G.. Simple homotopy types and finite spaces. Adv. Math. 218 (2008), 87–104.CrossRefGoogle Scholar
Batzies, E. and Welker, V.. Discrete Morse theory for cellular resolutions. J. Reine Angew. Math. 543 (2002), 147–168.Google Scholar
Bestvina, M.. PL Morse theory. Math. Commun. 13 (2008), 149–162.Google Scholar
Bestvina, M. and Brady, N.. Morse theory and finiteness properties of groups. Invent. Math. 129 (1997), 445–470.CrossRefGoogle Scholar
Bott, R.. The stable homotopy of the classical groups. Ann. Math. 70 (1959), 313–337.CrossRefGoogle Scholar
Brown, R.. Topology and groupoids, Third edition of Elements of modern topology, pp. xxvi+512 (Charleston, SC: BookSurge LLC, 2006).Google Scholar
Bux, K. U.. Orbit spaces of subgroup complexes, Morse theory, and a new proof of a conjecture of Webb. Topol. Proc. 24 (1999), 39–51.Google Scholar
Chari, M.. On discrete Morse functions and combinatorial decompositions. Discrete Math. 217 (2000), 101–113.CrossRefGoogle Scholar
Forman, R.. Morse theory for cell complexes. Adv. Math. 134 (1998), 90–145.CrossRefGoogle Scholar
Forman, R.. Witten–Morse theory for cell complexes. Topology 37 (1998), 945–979.CrossRefGoogle Scholar
Forman, R.. A user's guide to discrete Morse theory. Semin. Lothar. Comb. 48 (2002), B48c.Google Scholar
McCord, M. C.. Singular homology groups and homotopy groups of finite topological spaces. Duke Math. J. 33 (1966), 465–474.CrossRefGoogle Scholar
Milnor, J.. Morse theory. Based on lecture notes by M. Spivak and R. Wells. Annals of Mathematics Studies, vol. 51, pp. vi+153 (Princeton, NJ: Princeton University Press, 1963).Google Scholar
Milnor, J.. Lectures on the h-cobordism theorem, pp. v+116 (Princeton, NJ: Princeton University Press, 1965).CrossRefGoogle Scholar
Minian, E. G.. Some remarks on Morse theory for posets, homological Morse theory and finite manifolds. Topol. Appl. 159 (2012), 2860–2869.CrossRefGoogle Scholar
Mischaikow, K. and Nanda, V.. Morse theory for filtrations and efficient computation of persistent homology. Discrete Comput. Geom. 50 (2013), 330–353.CrossRefGoogle Scholar
Mrozek, M.. Conley–Morse–Forman theory for combinatorial multivector fields on Lefschetz complexes. Found. Comput. Math. 17 (2017), 1585–1633.CrossRefGoogle Scholar
Shareshian, J.. Discrete Morse theory for complexes of 2-connected graphs. Topology 40 (2001), 681–701.CrossRefGoogle Scholar
Stong, R. E.. Finite topological spaces. Trans. Am. Math. Soc. 123 (1966), 325–340.CrossRefGoogle Scholar
Zaremsky, M.. Bestvina–Brady discrete Morse theory and Vietoris–Rips complexes. Am. J. Math. (to appear).Google Scholar