Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-27T05:47:02.926Z Has data issue: false hasContentIssue false
  • English
  • Français

Invariant measures and large deviation principles for stochastic Schrödinger delay lattice systems

Part of: Stochastic analysis Limit theorems Infinite-dimensional dissipative dynamical systems

Published online by Cambridge University Press:  04 March 2024

Zhang Chen ,
Xiaoxiao Sun  and
Bixiang Wang
Zhang Chen
Affiliation:
School of Mathematics, Shandong University, Jinan 250100, People's Republic of China (zchen@sdu.edu.cn, xsun@mail.sdu.edu.cn)
Xiaoxiao Sun
Affiliation:
School of Mathematics, Shandong University, Jinan 250100, People's Republic of China (zchen@sdu.edu.cn, xsun@mail.sdu.edu.cn)
Bixiang Wang
Affiliation:
Department of Mathematics, New Mexico Institute of Mining and Technology, Socorro 87801, NM, USA (bwang@nmt.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper is concerned with stochastic Schrödinger delay lattice systems with both locally Lipschitz drift and diffusion terms. Based on the uniform estimates and the equicontinuity of the segment of the solution in probability, we show the tightness of a family of probability distributions of the solution and its segment process, and hence the existence of invariant measures on $l^2\times L^2((-\rho,\,0);l^2)$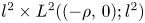 with $\rho >0$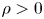. We also establish a large deviation principle for the solutions with small noise by the weak convergence method.

Keywords

Stochastic Schrödinger lattice systemtime delayinvariant measuretightnesslarge deviation principleLaplace principleweak convergence

MSC classification

Primary: 37L40: Invariant measures
Secondary: 37L55: Infinite-dimensional random dynamical systems; stochastic equations 60F10: Large deviations 60H10: Stochastic ordinary differential equations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 42
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bao, J. and Yuan, C.. Large deviations for neutral functional SDEs with jumps. Stochastics 87 (2015), 48–70.CrossRefGoogle Scholar
Bates, P. W., Lu, K. and Wang, B.. Attractors of non-autonomous stochastic lattice systems in weighted spaces. Phys. D 289 (2014), 32–50.CrossRefGoogle Scholar
Bessaih, H., Garrido-Atienza, M. J., Han, X. and Schmalfuss, B.. Stochastic lattice dynamical systems with fractional noise. SIAM J. Math. Anal. 49 (2017), 1495–1518.CrossRefGoogle Scholar
Billingsley, P.. Convergence of Probability Measures (New York, Wiley, 1999).CrossRefGoogle Scholar
Boué, M. and Dupuis, P.. A variational representation for certain functionals of Brownian motion. Ann. Probab. 26 (1998), 1641–1659.CrossRefGoogle Scholar
Budhiraja, A., Chen, J. and Dupuis, P.. Large deviations for stochastic partial differential equations driven by a Poisson random measure. Stoch. Process. Appl. 123 (2013), 523–560.CrossRefGoogle Scholar
Budhiraja, A. and Dupuis, P.. A variational representation for positive functionals of infinite dimensional Brownian motion. Probab. Math. Statist. 20 (2000), 39–61.Google Scholar
Budhiraja, A., Dupuis, P. and Maroulas, V.. Large deviations for infinite dimensional stochastic dynamical systems. Ann. Probab. 36 (2008), 1390–1420.CrossRefGoogle Scholar
Caraballo, T., Morillas, F. and Valero, J.. Attractors of stochastic lattice dynamical systems with a multiplicative noise and non-Lipschitz nonlinearities. J. Differ. Equ. 253 (2012), 667–693.CrossRefGoogle Scholar
Cerrai, S. and Debussche, A.. Large deviations for the two-dimensional stochastic Navier–Stokes equation with vanishing noise correlation. Ann. Inst. Henri Poincaré Probab. Statist. 55 (2019), 211–236.CrossRefGoogle Scholar
Chen, Y. and Gao, H.. Well-posedness and large deviations for a class of SPDEs with Lévy noise. J. Differ. Equ. 263 (2017), 5216–5252.CrossRefGoogle Scholar
Chen, Z., Li, X. and Wang, B.. Invariant measures of stochastic delay lattice systems. Discrete Contin. Dyn. Syst. Ser. B 26 (2021), 3235–3269.Google Scholar
Chen, Z., Sun, X. and Yang, D.. Ergodicity and approximations of invariant measures for stochastic lattice systems with Markovian switching. Stoch. Anal. Appl. 41 (2023), 1155–1190.CrossRefGoogle Scholar
Chen, Z. and Wang, B.. Existence, exponential mixing and convergence of periodic measures of fractional stochastic delay reaction-diffusion equations on $\mathbb {R}^n$. J. Differ. Equ. 336 (2022), 505–564.CrossRefGoogle Scholar
Chen, Z. and Wang, B.. Weak mean attractors and invariant measures for stochastic Schrödinger delay lattice systems. J. Dyn. Differ. Equ. 35 (2023), 3201–3240.CrossRefGoogle Scholar
Chen, Z., Wang, B. and Yang, L.. Invariant measures of stochastic Schrödinger delay lattice systems (in Chinese). Sci. Sin. Math. 52 (2022), 1015–1032. https://www.sciengine.com/SSM/doi/10.1360/SCM-2021-0034.Google Scholar
Da Prato, G. and Zabczyk, J.. Stochastic Equations in Infinite Dimensions (Cambridge, Cambridge University Press, 1992).CrossRefGoogle Scholar
Dupuis, P. and Ellis, R. S.. A Weak Convergence Approach to the Theory of Large Deviations (New York, Wiley-Interscience, 1997).CrossRefGoogle Scholar
Freidlin, M. I. and Wentzell, A. D.. Random Perturbations of Dynamical Systems (New York, Springer, 1984).CrossRefGoogle Scholar
Han, X., Shen, W. and Zhou, S.. Random attractors for stochastic lattice dynamical systems in weighted spaces. J. Differ. Equ. 250 (2011), 1235–1266.CrossRefGoogle Scholar
Jin, D., Chen, Z. and Zhou, T., Large deviations principle for stochastic delay differential equations with super-linearly growing coefficients, (2022). arXiv:2201.00143.Google Scholar
Li, D., Lin, Y. and Pu, Z.. Non-autonomous stochastic lattice systems with Markovian switching. Discrete Contin. Dyn. Syst. 43 (2023), 1860–1877.CrossRefGoogle Scholar
Li, D., Wang, B. and Wang, X.. Periodic measures of stochastic delay lattice systems. J. Differ. Equ. 272 (2021), 74–104.CrossRefGoogle Scholar
Lin, Y. and Li, D.. Limiting behavior of invariant measures of highly nonlinear stochastic retarded lattice systems. Discrete Contin. Dyn. Syst. Ser. B 27 (2022), 7561–7590.CrossRefGoogle Scholar
Liu, W.. Large deviations for stochastic evolution equations with small multiplicative noise. Appl. Math. Optim. 61 (2010), 27–56.CrossRefGoogle Scholar
Lipshutz, D.. Exit time asymptotics for small noise stochastic delay differential equations. Discrete Contin. Dyn. Syst. 38 (2018), 3099–3138.CrossRefGoogle Scholar
Mohammed, Salah-Eldin A. and Zhang, T.. Large deviations for stochastic systems with memory. Discrete Contin. Dyn. Syst. Ser. B 6 (2006), 881–893.Google Scholar
Röckner, M., Zhang, T. and Zhang, X.. Large deviations for stochastic tamed 3D Navier–Stokes equations. Appl. Math. Optim. 61 (2010), 267–285.CrossRefGoogle Scholar
Sritharan, S. S. and Sundar, P.. Large deviations for the two dimensional Navier–Stokes equations with multiplicative noise. Stoch. Process. Appl. 116 (2006), 1636–1659.CrossRefGoogle Scholar
Suo, Y. and Yuan, C.. Large deviations for neutral stochastic functional differential equations. Commun. Pure Appl. Anal. 19 (2020), 2369–2384.CrossRefGoogle Scholar
Wang, B.. Dynamics of stochastic reaction-diffusion lattice systems driven by nonlinear noise. J. Math. Anal. Appl. 477 (2019), 104–132.CrossRefGoogle Scholar
Wang, B. and Wang, R.. Asymptotic behavior of stochastic Schrödinger lattice systems driven by nonlinear noise. Stoch. Anal. Appl. 38 (2020), 213–237.CrossRefGoogle Scholar
Wang, B., Large deviation principles of stochastic reaction-diffusion lattice systems. Discrete Contin. Dyn. Syst. Ser. B 29 (2024), 1319–1343.Google Scholar
Wang, R.. Long-time dynamics of stochastic lattice plate equations with nonlinear noise and damping. J. Dyn. Differ. Equ. 33 (2021), 767–803.CrossRefGoogle Scholar
Wang, W. and Duan, J.. Reductions and deviations for stochastic partial differential equations under fast dynamical boundary conditions. Stoch. Anal. Appl. 27 (2009), 431–459.CrossRefGoogle Scholar
Wang, X., Kloeden, P. E. and Han, X.. Stochastic dynamics of a neural field lattice model with state dependent nonlinear noise. Nonlinear Differ. Equ. Appl. 28 (2021), 43.CrossRefGoogle Scholar
Wang, Y., Wu, F. and Mao, X.. Stability in distribution of stochastic functional differential equations. Syst. Control Lett. 132 (2019), 104513.CrossRefGoogle Scholar