Published online by Cambridge University Press: 12 August 2021
In this paper, from the property of Killing for structure Jacobi tensor 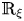 $\mathbb {R}_{\xi }$, we introduce a new notion of cyclic parallelism of structure Jacobi operator
$\mathbb {R}_{\xi }$, we introduce a new notion of cyclic parallelism of structure Jacobi operator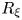 $R_{\xi }$ on real hypersurfaces in the complex two-plane Grassmannians. By virtue of geodesic curves, we can give the equivalent relation between cyclic parallelism of
$R_{\xi }$ on real hypersurfaces in the complex two-plane Grassmannians. By virtue of geodesic curves, we can give the equivalent relation between cyclic parallelism of 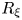 $R_{\xi }$ and Killing property of
$R_{\xi }$ and Killing property of 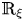 $\mathbb {R}_{\xi }$. Then, we classify all Hopf real hypersurfaces with cyclic parallel structure Jacobi operator in complex two-plane Grassmannians.
$\mathbb {R}_{\xi }$. Then, we classify all Hopf real hypersurfaces with cyclic parallel structure Jacobi operator in complex two-plane Grassmannians.