Hostname: page-component-77c89778f8-sh8wx Total loading time: 0 Render date: 2024-07-16T16:12:02.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Classification of simple Harish–Chandra modules over the Ovsienko–Roger superalgebra

Part of: Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  14 March 2023

Munayim Dilxat ,
Liangyun Chen  and
Dong Liu
Munayim Dilxat
Affiliation:
College of Mathematics and System Sciences, Xinjiang University, Urumqi 830046, Xinjiang, China (munayim@stu.xju.edu.cn)
Liangyun Chen
Affiliation:
School of Mathematics and Statistics, Northeast Normal University, Changchun 130024, China (chenly640@nenu.edu.cn)
Dong Liu
Affiliation:
Department of Mathematics, Huzhou University, Zhejiang Huzhou 313000, China (liudong@zjhu.edu.cn)
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we give a new method to classify all simple cuspidal modules for the $\mathbb {Z}$-graded and $1/2\mathbb {Z}$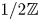-graded Ovsienko–Roger superalgebras. Using this result, we classify all simple Harish–Chandra modules over some related Lie superalgebras, including the $N=1$ 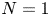BMS$_3$ superalgebra, the super $W(2,2)$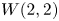, etc.

Keywords

Virasoro algebraOvsienko–Roger superalgebraHarish–Chandra modulesCuspidal modules

MSC classification

Primary: 17B10: Representations, algebraic theory (weights)
Secondary: 17B20: Simple, semisimple, reductive (super)algebras 17B65: Infinite-dimensional Lie (super)algebras 17B66: Lie algebras of vector fields and related (super) algebras 17B68: Virasoro and related algebras
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 154 , Issue 2 , April 2024 , pp. 483 - 493
Check for updates
Copyright
Copyright © The Author(s), 2023. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arbarello, E., De Concini, C., Kac, V. and Procesi, C.. Moduli spaces of curves and representation theory. Commun. Math. Phys. 117 (1988), 1–36.Google Scholar
Bagchi, A.. The BMS/GCA correspondence. Phys. Rev. Lett. 105 (2010), 171601.Google Scholar
Barnich, G., Donnay, L., Matulich, J. and Troncoso, R.. Asymptotic symmetries and dynamics of three-dimensional flat supergravity. JHEP. 08 (2014), 071.Google Scholar
Billig, Y.. Jet modules. Canad. J. Math. 59 (2007), 721–729.Google Scholar
Billig, Y. and Futorny, V.. Classification of irreducible representations of Lie algebra of vector fields on a torus. J. Reine Angew. Math. 720 (2016), 199–216.Google Scholar
Billig, Y., Futorny, V., Iohara, K. and Kashuba, I.. Classification of simple strong Harish-Chandra $W(m, n)$-modules. e-print arXiv:2006.05618.Google Scholar
Bondi, H., Van der Burg, M. G. J. and Metzner, A. W. K.. Gravitational waves in general relativity, 7. Waves from axisymmetric isolated systems. Proc. Roy. Soc. Lond. A. 269 (1962), 21.Google Scholar
Cai, Y., Liu, D. and Lü, R.. Classification of simple Harish-Chandra modules over the $N=1$ Ramond algebra. J. Algebra. 567 (2021), 114–127.Google Scholar
Cai, Y. and Lü, R.. Classification of simple Harish-Chandra modules over the Neveu-Schwarz algebra and its contact subalgebra. J. Pure Appl. Algebra. 226 (2022), 106866.Google Scholar
Cai, Y., Lü, R. and Wang, Y.. Classification of simple Harish-Chandra modules for map (super)algebras related to the Virasoro algebra. J. Algebra. 570 (2021), 397–415.Google Scholar
Dilxat, M., Gao, S. and Liu, D.. Whittaker modules for the $N=1$ super-BMS$_3$ algebra. J. Algebra Appl. (2023), doi:10.1142/S0219498824500889.Google Scholar
Fuks, D. B.. Cohomology of Infinite-Dimensional Lie Algebras [in Russian] (Moscow: Nauka, 1984). English transl. Plenum, New York (1986).Google Scholar
Ge, Y.. Super Camassa-Holm-type systems associated to the Kuper-Ramond-Schwarz superalgebra. J. Math. Phys. 61 (2020), 103501.CrossRefGoogle Scholar
Guo, X., Lü, R. and Zhao, K.. Simple Harish-Chandra modules, intermediate series modules, and Verma modules over the loop-Virasoro algebra. Forum Math. 23 (2011), 1029–1052.Google Scholar
He, Y., Liu, D. and Wang, Y.. Simple Harish-Chandra modules over the super affine-Virasoro algebras. e-print arxiv:2112.07448.Google Scholar
Kac, V.. Some problems of infinite-dimensional Lie algebras and their representations. Lecture Notes Math. 933 (1982), 117–126.Google Scholar
Kaplansky, I. and Santharoubane, L. J.. Harish-Chandra modules over the Virasoro algebra. Infinite-dimensional groups with applications (Berkeley, Calif. 1984), pp. 217–231. Math. Sci. Res. Inst. Publ., 4, Springer, New York, (1985).Google Scholar
Liu, D.. Classification of Harish-Chandra modules over some Lie algebras related to the Virasoro algebra. J. Algebra. 447 (2016), 548–559.Google Scholar
Liu, D., Pei, Y. and Xia, L.. Simple restricted modules for Neveu-Schwarz algebra. J. Algebra. 546 (2020), 341–356.Google Scholar
Liu, D., Pei, Y. and Xia, L.. A Category of restricted modules for the Ovisenko-Roger algebra. Algebr. Represent. Theo. 25 (2022), 777–791.Google Scholar
Liu, D., Pei, Y. and Xia, L.. Classification of simple weight modules for the $N=2$ superconformal algebra. e-print arXiv:1904.08578v1.Google Scholar
Lü, R. and Zhao, K.. Classification of irreducible weight modules over the twisted Heisenberg-Virasoro algebra. Commun. Contemp. Math. 12 (2010), 183–205.Google Scholar
Mathieu, O.. Classification of Harish-Chandra modules over the Virasoro Lie algebra. Invent. Math. 107 (1992), 225–234.Google Scholar
Ovsienko, V. and Roger, C.. Extension of Virasoro group and Virasoro algebra by modules of tensor densities on $S^1$. Funct. Anal. Appl. 30 (1996), 290–291.Google Scholar
Rao, S. E.. Partial classification of modules for Lie algebra of diffeomorphisms of $d$-dimensional torus. J. Math. Phys. 45 (2004), 3322–3333.Google Scholar
Su, Y.. Classification of Harish-Chandra modules over the super-Virasoro algebras. Commun. Algebra. 23 (1995), 3653–3675.CrossRefGoogle Scholar
H. Wang, H. Fa and J. Li. Representations of super W(2,2) algebra $\frak L$. e-print arxiv:1705.09452.Google Scholar
Wang, Y., Chen, Z. and Bai, C.. Classification of Balinsky-Novikov superalgebras with dimension $2|2$. J. Phys. A: Math. Theor. 45 (2012), 225201.Google Scholar
Wang, Y., Geng, Q. and Chen, Z.. The superalgebra of $W(2,2)$ and its modules of the intermediate series. Commun. Algebra. 45 (2016), 749–763.Google Scholar
Xue, Y. and Lü, R.. Simple weight modules with finite-dimensional weight spaces over the Witt superalgebras. J. Algebra. 574 (2021), 92–116.Google Scholar
Zhang, W. and Dong, C.. $W$-algebra W(2,2) and the vertex operator algebra $L({1}/2,0)\otimes L(1/2,0)$. Commun. Math. Phys. 285 (2009), 991–1004.Google Scholar