Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-26T21:37:44.530Z Has data issue: false hasContentIssue false
  • English
  • Français

Analytic continuation and boundary continuity of functions of several complex variables

Published online by Cambridge University Press:  14 November 2011

Edgar Lee Stout
Edgar Lee Stout
Affiliation:
Department of Mathematics, University of Washington, Seattle, Washington 98195, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

This note treats some questions about analytic continuation in several variables. The first theorem in effect determines the envelops of holomorphy of certain domains in ℂn. The second main result is a continuity theorem: If a bounded holomorphic function f on a convex domain ∆ in ℂn has boundary values that are continuous on the complement (in b∆) of a set of the form int∏ (b∆∩∏) where ∏ is a real hyperplane in ℂn that misses ∆, then f is continuous on 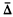. In addition, we obtain what may be regarded as a local version of the theorem in our earlier paper concerning the one-dimensional extension property. Our methods depend on Hartogs' theorem (n ≧ 3) and directly on the BochnerMartinelli formula (n = 2).

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 89 , Issue 1-2 , 1981 , pp. 63 - 74
Copyright
Copyright © Royal Society of Edinburgh 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Agranovskii, M. L. and Val'skii, R. É.. Maximality of invariant algebras of functions. Siberian Math. J. 12 (1971), 1–7.CrossRefGoogle Scholar
2Aytuna, A.. Some Results on Hp -Spaces on Strictly Pseudoconvex Domains (Dissertation, Univ. of Washington, Seattle, 1976).Google Scholar
3Alexander, H.. A note on polynomial hulls. Proc. Amer. Math. Soc. 33 (1972), 389–391.CrossRefGoogle Scholar
4Basener, R. F.. Complementary components of polynomial hulls. Proc. Amer. Math. Soc. 69 (1978), 230–232.CrossRefGoogle Scholar
5Bremmerman, H. J.. Complex convexity. Trans. Amer. Math. Soc. 82 (1956), 17–51.CrossRefGoogle Scholar
6Dahlberg, B. E. J.. On estimates of harmonic functions. Arch. Rational Mech. Anal. 65 (1977), 275–288.CrossRefGoogle Scholar
7Duren, P. L.. Theory of Hp Spaces (New York: Academic Press, 1970).Google Scholar
8Federer, H.. Geometric Measure Theory (New York: Springer-Verlag, 1969).Google Scholar
9Glicksberg, I.. Boundary continuity of some holomorphic functions. Pacific J. Math. 80 (1979), 425–434.CrossRefGoogle Scholar
10Goluzin, G. M.. Geometric Theory of Functions of a Complex Variable (Providence, R.I.: Amer. Math. Soc, 1969).CrossRefGoogle Scholar
11Gunning, R. C. and Rossi, H.. Analytic Functions of Several Complex Variables (Englewood Cliffs, N.J.: Prentice-Hall, 1965).Google Scholar
12Harvey, F. R. and Lawson, H. B.. On boundaries of complex analytic varieties, I. Ann. of Math. 102 (1975), 223–290.CrossRefGoogle Scholar
13Hunt, R. A. and Wheeden, R. L.. On the boundary values of harmonic functions. Trans. Amer. Math. Soc. 132 (1968), 307–322.CrossRefGoogle Scholar
14Kajiwara, J. and Sakai, E.. Generalization of Levi-Oka's theorem concerning meromorphic functions. Nagoya Math. J. 29 (1967), 75–84.CrossRefGoogle Scholar
15Priwalow, I. I..Randeigenschaften Analytischer Funktionen (Berlin: VEB Deutscher Verlag der Wissenschaften, 1956).Google Scholar
16Stout, E. L.. The boundary values of holomorphic functions of several complex variables. Duke Math. J. 44 (1977), 105–108.CrossRefGoogle Scholar
17Vladimirov, V. S.. Les Fonctions de Plusieurs Variables Complexes (Paris: Dunod, 1967).Google Scholar