Article contents
A simpler proof of two inequalities of Brodlie and Everitt
Published online by Cambridge University Press: 14 November 2011
Synopsis
In 1975 K. W. Brodie and W. N. Everitt dealt with integral inequalities of the form
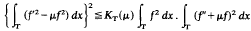
in the two cases T = ℝ, T = ℝ+, and obtained the best possible constants KT(μ) for all μ ε ℝ. The proof was not elementary, but an elementary proof was given in 1977 by E. T. Copson. This note shows how Copson's method can be greatly simplified so as to obtain the results in a more straightforward manner.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 84 , Issue 3-4 , 1979 , pp. 259 - 261
- Copyright
- Copyright © Royal Society of Edinburgh 1979
References
- 4
- Cited by




