Article contents
On non-autonomously forced Burgers equation with periodic and Dirichlet boundary conditions
Published online by Cambridge University Press: 14 March 2019
Abstract
We study the non-autonomously forced Burgers equation
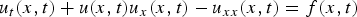 $$u_t(x,t) + u(x,t)u_x(x,t)-u_{xx}(x,t) = f(x,t)$$
$$u_t(x,t) + u(x,t)u_x(x,t)-u_{xx}(x,t) = f(x,t)$$
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 4 , August 2020 , pp. 2025 - 2054
- Copyright
- Copyright © Royal Society of Edinburgh 2019
References
- 2
- Cited by



