Hostname: page-component-84b7d79bbc-c654p Total loading time: 0 Render date: 2024-07-26T02:39:55.006Z Has data issue: false hasContentIssue false
  • English
  • Français

On an inequality of Hardy-Littlewood type: I

Published online by Cambridge University Press:  14 November 2011

W. D. Evans  and
W. N. Everitt
W. D. Evans
Affiliation:
Department of Pure Mathematics, University College, Cardiff CF1 1XL, Wales
W. N. Everitt
Affiliation:
Department of Mathematics, University of Birmingham, Birmingham B15 2TT, England
Get access Rights & Permissions [Opens in a new window]

Synopsis

This paper gives a complete analysis of the integral inequality

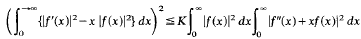
where the integral on the left may be only conditionally convergent. It is shown that the best possible number K is 4 and all cases of equality are identified in terms of Hankel-Bessel functions of order ⅓.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 101 , Issue 1-2 , 1985 , pp. 131 - 140
Copyright
Copyright © Royal Society of Edinburgh 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bennewitz, C.. A general version of the Hardy-Littlewood-Polya-Everitt (HELP) inequality. Proc. Roy. Soc. Edinburgh Sect. A 97 (1984), 9–20.CrossRefGoogle Scholar
2Bennewitz, C. and Everitt, W. N.. Some remarks on the Titchmarsh-Weyl m-coefficient. Tribute to Åke Pleijel, 49–108 (Proceedings of the Pleijel Conference, Uppsala, 1979, published by the Department of Mathematics, University of Uppsala, Sweden, 1980).Google Scholar
3Evans, W. D. and Everitt, W. N.. A return to the Hardy-Littlewood integral inequality. Proc. Roy. Soc. London Ser. A 380 (1982), 447–486.Google Scholar
4Evans, W. D. and Zettl, A.. Norm inequalities involving derivatives. Proc. Roy. Soc. Edinburgh Sect. A 82 (1978), 51–70.CrossRefGoogle Scholar
5Everitt, W. N.. On an extension to an integro-differential inequality of Hardy, Littlewood and Polya. Proc. Roy. Soc. Edinburgh Sect. A 69 (1972), 295–333.Google Scholar
6Everitt, W. N. and Jones, D. S.. On an integral inequality. Proc. Roy. Soc. London Ser. A 357 (1977), 271–288.Google Scholar
7Everitt, W. N. and Zettl, A.. On a class of integral inequalities. J. London Math. Soc. 17 (1978), 291–303.CrossRefGoogle Scholar
8Everitt, W. N., Giertz, M. and McLeod, J. B.. On the strong and weak limit-point classification of second-order differential expressions. Proc. London Math. Soc. 29 (1974), 142–158.CrossRefGoogle Scholar
9Phóng, Vũ Qùôc. On inequalities for powers of linear operators and for quadratic forms. Proc. Roy. Soc. Edinburgh Sect. A 89 (1981), 25–50.CrossRefGoogle Scholar
10Russell, A.. Integral inequalities and spectral theory of certain ordinary differential operators. Ph.D. thesis; University of Dundee, Scotland (1975).Google Scholar
11Titchmarsh, E. C.. Eigenfunction expansions, Part 1 (2nd edn) (Oxford University Press, 1962).Google Scholar
12Titchmarsh, E. C.. Some problems on perturbation theory III. Proc. Roy. Soc. London Ser. A 207 (1951), 321–328.Google Scholar
13Watson, G. N.. A treatise on the theory of Bessel functions (Cambridge University Press, 1944).Google Scholar