Article contents
On a class of interpolation series
Published online by Cambridge University Press: 14 November 2011
Synopsis
This paper deals with a class of interpolation series of the form
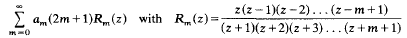
called R-series. It is equiconvergent with the Dirichlet series
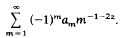
If the nth Legendre polynomial for the interval (0,1) is denoted by (−1)nLn(t), then the bilinear formula
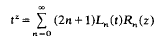
serves as generating function for the Rn(z). It also leads in easy steps to R-series expansions for rational functions.
Lagrange [7] has shown that a function holomorphic and of finite rate of growth in a right half-plane can be expanded in an R-series whose abscissa of convergence is limited by the rate of growth of f(z). The converse problem is attacked in Theorem 2 below where it is shown that
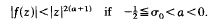
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 84 , Issue 3-4 , 1979 , pp. 283 - 307
- Copyright
- Copyright © Royal Society of Edinburgh 1979
References
- 2
- Cited by




