Article contents
Limit theorems for additive functionals of continuous time random walks
Published online by Cambridge University Press: 28 May 2020
Abstract
For a continuous-time random walk X = {Xt, t ⩾ 0} (in general non-Markov), we study the asymptotic behaviour, as t → ∞, of the normalized additive functional 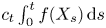 $c_t\int _0^{t} f(X_s)\,{\rm d}s$, t⩾ 0. Similarly to the Markov situation, assuming that the distribution of jumps of X belongs to the domain of attraction to α-stable law with α > 1, we establish the convergence to the local time at zero of an α-stable Lévy motion. We further study a situation where X is delayed by a random environment given by the Poisson shot-noise potential:
$c_t\int _0^{t} f(X_s)\,{\rm d}s$, t⩾ 0. Similarly to the Markov situation, assuming that the distribution of jumps of X belongs to the domain of attraction to α-stable law with α > 1, we establish the convergence to the local time at zero of an α-stable Lévy motion. We further study a situation where X is delayed by a random environment given by the Poisson shot-noise potential: 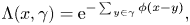 $\Lambda (x,\gamma )= {\rm e}^{-\sum _{y\in \gamma } \phi (x-y)},$ where
$\Lambda (x,\gamma )= {\rm e}^{-\sum _{y\in \gamma } \phi (x-y)},$ where 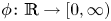 $\phi \colon \mathbb R\to [0,\infty )$ is a bounded function decaying sufficiently fast, and γ is a homogeneous Poisson point process, independent of X. We find that in this case the weak limit has both ‘quenched’ component depending on Λ, and a component, where Λ is ‘averaged’.
$\phi \colon \mathbb R\to [0,\infty )$ is a bounded function decaying sufficiently fast, and γ is a homogeneous Poisson point process, independent of X. We find that in this case the weak limit has both ‘quenched’ component depending on Λ, and a component, where Λ is ‘averaged’.
Keywords
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 151 , Issue 2 , April 2021 , pp. 799 - 820
- Copyright
- Copyright © The Author(s), 2020. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh
References
- 2
- Cited by





