Article contents
Hausdorff operators on holomorphic Hardy spaces and applications
Published online by Cambridge University Press: 30 January 2019
Abstract
The aim of this paper is to characterize the non-negative functions φ defined on (0,∞) for which the Hausdorff operator
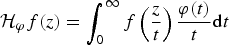 $${\rm {\cal H}}_\varphi f(z) = \int_0^\infty f \left( {\displaystyle{z \over t}} \right)\displaystyle{{\varphi (t)} \over t}{\rm d}t$$
$${\rm {\cal H}}_\varphi f(z) = \int_0^\infty f \left( {\displaystyle{z \over t}} \right)\displaystyle{{\varphi (t)} \over t}{\rm d}t$$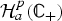 ${\rm {\cal H}}_a^p ({\open C}_ + )$,
${\rm {\cal H}}_a^p ({\open C}_ + )$, 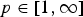 $p\in [1,\infty ]$. The corresponding operator norms and their applications are also given.
$p\in [1,\infty ]$. The corresponding operator norms and their applications are also given.
MSC classification
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 150 , Issue 3 , June 2020 , pp. 1095 - 1112
- Copyright
- Copyright © 2019 The Royal Society of Edinburgh
References
- 6
- Cited by




