Hostname: page-component-77c89778f8-n9wrp Total loading time: 0 Render date: 2024-07-17T17:48:17.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Critical diffusion exponents for self-similar blow-up solutions of a quasilinear parabolic equation with an exponential source

Published online by Cambridge University Press:  14 November 2011

Chris J. Budd  and
Victor A. Galaktionov
Chris J. Budd
Affiliation:
School of Mathematics, University of Bath, Bath, BA2 7AY, U.K.
Victor A. Galaktionov
Affiliation:
School of Mathematics, University of Bath, Bath, BA2 7AY, U.K.
Get access Rights & Permissions [Opens in a new window]

Extract

We study the self-similar solutions of the quasilinear parabolic equation

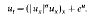
We show that there is an exponent

such that if σ> then the equation admits a countable set {uk(x, t)} of self-similar blow-up solutions. These solutions have the form

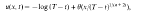
where T> 0 is a finite blow-up time, θ(ξ) solves a nonlinear ODE and each function uk(x, t) is nonconstant in a neighbourhood of the origin and has exactly k maxima and minima for x ≧ 0. There is a further critical exponent σ = ф such that if σ > ф there is a second set of self-similar solutions which are constant (in x) in a neighbourhood of the origin. We conjecture (and provide formal arguments and numerical evidence for) the existence of an infinite sequence σk→σ∞ of critical values, such that σ1 = 0 and uk exists only in the range σ>σk (when σ> 0 the equation has no nontrivial self-similar solutions). The proof of existence when σ>σ∞(σ>ф) is obtained by a combination of comparison and dynamical systems arguments and relates the existence of the self-similar solutions to a homoclinic bifurcation in an appropriate phase-space.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 126 , Issue 2 , 1996 , pp. 413 - 441
Copyright
Copyright © Royal Society of Edinburgh 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Ad'jutov, M. M. Ju., Klokov, A. and Mikhailov, A. P.. Self-similar thermal structures with contracting half-width. Differential Equations 19 (1983). 809–15.Google Scholar
2Andronov, A. A.. Leontovich, E. A., Gordon, I. I. and Majer, A. G.. Qualitative Theorv oj Second- Order Dynamical Systems (New York: Wiley. 1972).Google Scholar
3Bebernes, J. and Bricher, S.. Final time blowup profiles for semihnear parabolic equations via center manifold theory. SIAM J. Math. Anal. 23 (1992), 852–69.CrossRefGoogle Scholar
4Bebernes, J., Bricher, S. and Galaktionov, V. A.. Asymptotics of blow-up for weakly quasilinear parabolic problems. Nonlinear Anal. 23 (1994), 489–514.CrossRefGoogle Scholar
5Bebernes, J. and Eberly, D.. Mathematical Problems from Combustion Theory. Applied Mathematical Sciences 83 (Berlin: Springer, 1989).CrossRefGoogle Scholar
6Bebernes, J. and Troy, W.. On the non-existence of solutions to the Kassoy problem in dimension 1. SIAM. 1. Math. Anal. 18 (1987). 1157–62.CrossRefGoogle Scholar
7Bressan, A.. On the asymptotic shape of blow-up. Indiana Univ. Math. J. 39 (1990), 947–60.CrossRefGoogle Scholar
8Bressan, A.. Stable blow-up patterns. J. Differential Equations 98 (1992), 57–75.CrossRefGoogle Scholar
9Budd, C.. W, J.. , Dold and Galaktionov, V. A.. Self-similar blow-up for quasilinear parabolic equation with gradient diffusion and exponential source (Bristol University report AM-92–09, 1992).Google Scholar
10Budd, C and Galaktionov, V. A.. Blow-up problems with quasi-linear gradient diffusivity (Bristol University Report AM-95-01, 1995).Google Scholar
11Budd, C. and Galaktionov, V. A.. Asymptotics of blow-up in quasilinear diffusion equations (in prep.).Google Scholar
12Cesari, L.. Asymptotic Behaviour and Stability Problems in Ordinary Differential Equations (New York: Academic Press. 1971).CrossRefGoogle Scholar
13Dold, J. W.. Analysis of the early stage of thermal runaway. Quart. J. Mech. Appl. Math. 38 (1985),361–87.CrossRefGoogle Scholar
14Eberly, D.. Non-existence for the Kassoy problem in dimension 1 and 2. J. Math. Anal. Appl. 129 (1988), 401–8.CrossRefGoogle Scholar
15Friedman, A.. Partial Differential Equations of Parabolic Txpe1 (Englewood Cliffs, NJ; Prentice Hall. 1964).Google Scholar
16Galaktionov, V. A.. Proof of the localization of unbounded solutions of the nonlinear parabolic equation ut = (uσux)x + uβ. Differential Equations 21 (1985), 11–18.Google Scholar
17Galaktionov, V. A., Kurdyumov, S. P., Posashkov, S. A. and Samarskii, A. A..Quasilinear parabolic equation with complex spectriem of unbounded self-similar solutions. In Mathematical Modelling. Processes in Nonlinear Media, 142–82 (Mowscow, Nauka: 1986 (in Russian); English translation: CRC Press Int., 1992).Google Scholar
18Galaktionov, V. A. and Posashkov, S. A.. Single point blow-up for A'-dimensional quasilinear equation with gradient diffusion and source. Indiana Univ. Math. J. 40 (1991), 1041–60.CrossRefGoogle Scholar
19Giga, Y.. On elliptic equations related to self-similar solutions for non-linear heat equations. Hiroshima Math.J. 16 (1986), 541–54.CrossRefGoogle Scholar
20Haraux, A. and Weissler, F. B.. Non-uniqueness for a semilinear initial value problem. Indiana Univ. Math. J. 31 (1982), 167–89.CrossRefGoogle Scholar
21Herrero, M. A. and Veláazquez, J. J. L.. Blow-up profiles in one-dimensional semi-linear problems. Comm. Partial Differential Equations 17 (1992), 205–19.CrossRefGoogle Scholar
22Herrero, M. A. and Velázquez, J. J. L.. Blow-up behavior of one-dimensional semilinear parabolic equations. Ann. Ins. H. Poincaré Anal. Non Linéaire 10 (1993). 131–89.CrossRefGoogle Scholar
23Samarskii, A. A.. Elenin, G. G., Zmitrenko, N. V., Kurdyunov, S. P. and Mikhailov, A. P.. Combustion of a non-linear medium in the form of complex structures. Dokl. Akad.Nauk SSSR, Ser. Math. Phxs. 237 (1977). 1330–3 (in Russian).Google Scholar
24Samarskii, A. A.. Galaktionov, V. A., Kurdyumov, S. P. and Mikhailov, A. P.. Blow-up in Quasilinear Parabolic Equations (Moscow, Nauka: 1987 (in Russian): English translation: Berlin: Walter de Gruytcr, 1995).CrossRefGoogle Scholar
25Velázquez, J. J. L.. Galaktionov, V. A. and Herrero, M. A.. The space structure near a blow-up point for semilinear heat equations, a formal approach. J. Vychisl. Matem. Mat em. Fir. 31 (1991). 399–411.Google Scholar