Hostname: page-component-77c89778f8-vpsfw Total loading time: 0 Render date: 2024-07-18T13:58:48.108Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcation of the travelling wave solutions in a perturbed (1 + 1)-dimensional dispersive long wave equation via a geometric approach

Part of: Stability theory Equations of mathematical physics and other areas of application Waves Hyperbolic equations and systems

Published online by Cambridge University Press:  25 April 2024

Hang Zheng  and
Yonghui Xia Open the ORCID record for Yonghui Xia [Opens in a new window]
Hang Zheng
Affiliation:
Department of Mathematics and Computer, Wuyi University, Wuyishan 354300, China (zhenghang513@zjnu.edu.cn, zhenghwyxy@163.com)
Yonghui Xia*
Affiliation:
School of Mathematics and Big Data Foshan University, Foshan 528000, China (xiadoc@163.com, yhxia@zjnu.cn)
*
*Corresponding author.
Get access Rights & Permissions [Opens in a new window]

Abstract

Choosing ${\kappa }$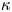 (horizontal ordinate of the saddle point associated to the homoclinic orbit) as bifurcation parameter, bifurcations of the travelling wave solutions is studied in a perturbed $(1 + 1)$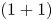-dimensional dispersive long wave equation. The solitary wave solution exists at a suitable wave speed $c$ 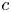for the bifurcation parameter ${\kappa }\in \left (0,1-\frac {\sqrt 3}{3}\right )\cup \left (1+\frac {\sqrt 3}{3},2\right )$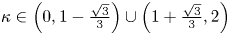, while the kink and anti-kink wave solutions exist at a unique wave speed $c^*=\sqrt {15}/3$ 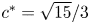for $\kappa =0$ or $\kappa =2$. The methods are based on the geometric singular perturbation (GSP, for short) approach, Melnikov method and invariant manifolds theory. Interestingly, not only the explicit analytical expression of the complicated homoclinic Melnikov integral is directly obtained for the perturbed long wave equation, but also the explicit analytical expression of the limit wave speed is directly given. Numerical simulations are utilized to verify our mathematical results.

Keywords

wave equationsolitary wave solutionsgeometric singular perturbation

MSC classification

Primary: 35Q35: PDEs in connection with fluid mechanics
Secondary: 35L05: Wave equation 74J30: Nonlinear waves 34D15: Singular perturbations
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , First View , pp. 1 - 28
Check for updates
Copyright
Copyright © The Author(s), 2024. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Buzzi, C. A., da Silva, P. R. and Teixeira, M.. Slow-fast systems on algebraic varieties bordering piecewise-smooth dynamical systems. Bull. Sci. Math. 136 (2012), 444–462.CrossRefGoogle Scholar
Chen, A. Y., Guo, L. N. and Deng, X. J.. Existence of solitary waves and periodic waves for a perturbed generalized BBM equation. J. Differ. Equ. 261 (2016), 5324–5349.CrossRefGoogle Scholar
Chen, A. Y., Guo, L. N. and Huang, W. T.. Existence of kink waves and periodic waves for a perturbed defocusing mKdV equation. Qual. Theory Dyn. Syst. 17 (2018), 495–517.CrossRefGoogle Scholar
Chen, C., Tang, X. and Lou, S.. Soliton excitations and periodic waves without dispersion relation in shallow water system. Chaos, Solitons Fractals 16 (2003), 27–35.CrossRefGoogle Scholar
Chen, Y. and Wang, Q.. A new general algebraic method with symbolic computation to construct new travelling wave solution for the $(1+1)$-dimensional dispersive long wave equation. Appl. Math. Comput. 168 (2005), 1189–1204.Google Scholar
Chen, X. F. and Zhang, X.. Dynamics of the predator-prey model with the Sigmoid functional response. Stud. Appl. Math. 147 (2021), 300–318.CrossRefGoogle Scholar
Chen, A. Y., Zhang, C. and Huang, W. T.. Monotonicity of limit wave speed of traveling wave solutions for a perturbed generalized KdV equation. Appl. Math. Lett. 121 (2021), 107381.CrossRefGoogle Scholar
Cheng, F. F. and Li, J.. Geometric singular perturbation analysis of Degasperis–Procesi equation with distributed delay. Discrete Contin. Dyn. Syst. 41 (2021), 967–985.CrossRefGoogle Scholar
Derks, G. and Gils, S.. On the uniqueness of traveling waves in perturbed Korteweg–de Vries equations. Jpn. J. Ind. Appl. Math. 10 (1993), 413–430.CrossRefGoogle Scholar
Du, Z. J. and Li, J.. Geometric singular perturbation analysis to Camassa–Holm Kuramoto–Sivashinsky equation. J. Differ. Equ. 306 (2022), 418–438.CrossRefGoogle Scholar
Du, Z. J., Li, J. and Li, X. W.. The existence of solitary wave solutions of delayed Camassa–Holm equation via a geometric approach. J. Funct. Anal. 275 (2018), 988–1007.CrossRefGoogle Scholar
Du, Z. J., Lin, X. J. and Yu, S. S.. Solitary wave and periodic wave for a generalized Nizhnik–Novikov–Veselov equation with diffusion term (in Chinese). Sci. Sin. Math. 50 (2020), 1–22.Google Scholar
Du, Z. J., Liu, J. and Ren, Y. L.. Traveling pulse solutions of a generalized Keller–Segel system with small cell diffusion via a geometric approach. J. Differ. Equ. 270 (2020), 1019–1042.CrossRefGoogle Scholar
Du, Z. J. and Qiao, Q.. The dynamics of traveling waves for a nonlinear Belousov–Zhabotinskii system. J. Differ. Equ. 269 (2020), 7214–7230.CrossRefGoogle Scholar
Fan, E. G.. Extended tanh-function method and its applications to nonlinear equations. Phys. Lett. A 277 (2000), 212–218.CrossRefGoogle Scholar
Fenichel, N.. Geometric singular perturbation theory for ordinary differential equations. J. Differ. Equ. 31 (1979), 53–98.CrossRefGoogle Scholar
Gradshteyn, I. S. and Ryzhik, I. M.. Table of integrals, series, and products. Translation edited and with a preface by Daniel Zwillinger and Victor Moll. 8th edn. pp. 94–95 (Amsterdam: Elsevier/Academic Press, 2015).Google Scholar
Guckenheimer, J. and Holmes, P.. Nonlinear oscillations, dynamical systems and bifurcations of vector fields. pp. 184–193 (New York: Sprigner-Verlag, 1997).Google Scholar
Han, M. A.. Bifurcation theory of limit cycles. pp. 252–289 (Beijing: Science Press, 2013).Google Scholar
Iuorio, A., Popović, N. and Szmolyan, P.. Singular perturbation analysis of a regularized MEMS Model. SIAM J. Appl. Dyn. Syst. 18 (2019), 661–708.CrossRefGoogle Scholar
Jones, C. K. R.. Geometric singular perturbation theory dynamical systems. Lecture Notes Math., vol. 1609, pp. 44–120 (Berlin: Springer, 1995).CrossRefGoogle Scholar
Li, J. B.. Singular nonlinear travelling wave equations: bifurcations and exact solutions (Beijing: Science, 2013).Google Scholar
Li, J., Lu, K. and Bates, P. W.. Normally hyperbolic invariant manifolds for random dynamical systems. Trans. Am. Math. Soc. 365 (2013), 5933–5966.CrossRefGoogle Scholar
Li, J., Lu, K. and Bates, P. W.. Invariant foliations for random dynamical systems. Discrete Contin. Dyn. Syst. 34 (2014), 3639–3666.CrossRefGoogle Scholar
Li, J., Lu, K. and Bates, P. W.. Geometric singular perturbation theory with real noise. J. Differ. Equ. 259 (2015), 5137–5167.CrossRefGoogle Scholar
Ogama, T.. Travelling wave solutions to a perturbed Korteweg–de Vries equation. Hiroshima Math. J. 24 (1994), 401–422.Google Scholar
Qiao, Q. and Zhang, X.. Traveling waves and their spectral stability in Keller–Segel system with large cell diffusion. J. Differ. Equ. 344 (2023), 807–845.CrossRefGoogle Scholar
Qiu, H. M., Zhong, L. N. and Shen, J. H.. Traveling waves in a generalized Camassa–Holm equation involving dual-power law nonlinearities. Commun. Nonlinear Sci. Numer. Simul. 106 (2022), 106106.CrossRefGoogle Scholar
Sun, X. B., Huang, W. T. and Cai, J. N.. Coexistence of the solitary and periodic waves in convecting shallow water fluid. Nonlinear Anal. Real World Appl. 53 (2020), 103067.CrossRefGoogle Scholar
Sun, X. B. and Yu, P.. Periodic traveling waves in a generalized BBM equation with weak backward diffusion and dissipation terms. Discrete Contin. Dyn. Syst. Ser. B 24 (2019), 965–987.Google Scholar
Szmolyan, P.. Transversal heteroclinic and homoclinic orbits in singular perturbation problems. J. Differ. Equ. 92 (1991), 252–281.CrossRefGoogle Scholar
Wang, Q., Chen, Y. and Zhang, H. Q.. A new Jacobi elliptic function rational expansion method and its application to $(1+1)$-dimensional dispersive long wave equation. Chaos, Solitons Fractals 23 (2005), 477–483.CrossRefGoogle Scholar
Wang, C. and Zhang, X.. Canards, heteroclinic and homoclinic orbits for a slow-fast predator-prey model of generalized Holling type III. J. Differ. Equ. 267 (2019), 3397–3441.CrossRefGoogle Scholar
Wen, Z. S.. On existence of kink and antikink wave solutions of singularly perturbed Gardner equation. Math. Methods Appl. Sci. 43 (2020), 4422–4427.Google Scholar
Wiggins, S.. Introduction to applied nonlinear systems and chaos (New York: Springer, 1990).CrossRefGoogle Scholar
Wu, X. and Ni, M. K.. Existence and stability of periodic contrast structure in reaction-advection-diffusion equation with discontinuous reactive and convective terms. Commun. Nonlinear Sci. Numer. Simul. 91 (2020), 105457.CrossRefGoogle Scholar
Wu, T. and Zhang, J.. On modeling nonlinear long wave. In Mathematics is for solving problems (eds. L. P. Cook, V. Roytbhurd, M. Tulin). p. 233 (Philadelphia, PA: SIAM, 1996).Google Scholar
Xu, C. H., Wu, Y. H., Tian, L. X. and Guo, B. L.. On kink and anti-kink wave solutions of Schrodinger equation with distributed delay. J. Appl. Anal. Comput. 8 (2018), 1385–1395.Google Scholar
Yan, W. F., Liu, Z. R. and Liang, Y.. Existence of solitary waves and periodic waves to a perturbed generalized KdV equation. Math. Model. Anal. 19 (2014), 537–555.CrossRefGoogle Scholar
Yang, Q. and Ni, M. K.. Asymptotics of the solution to a stationary piecewise-smooth reaction-diffusion equation with a multiple root of the degenerate equation. Sci. China Math. 65 (2022), 291–308.CrossRefGoogle Scholar
Zeng, X. and Wang, D. S.. A generalized extended rational expansion method and its application to (1+1)-dimensional dispersive long wave equation. Appl. Math. Comput. 212 (2009), 296–304.Google Scholar
Zhang, X.. Homoclinic, heteroclinic and periodic orbits of singularly perturbed systems. Sci. China Math. 62 (2019), 1687–1704.CrossRefGoogle Scholar
Zhang, L. J., Han, M. A., Zhang, M. J. and Khalique, C. M.. A new type of solitary wave solution of the mKdV equation under singular perturbations. Int. J. Bifurcation Chaos 30 (2020), 1–14.CrossRefGoogle Scholar
Zhang, L. J., Wang, J. D., Shchepakina, E. and Sobolev, V.. New type of solitary wave solution with coexisting crest and trough for a perturbed wave equation. Nonlinear Dyn. 106 (2021), 3479–3493.CrossRefGoogle Scholar
Zhu, K., Wu, Y. H., Yu, Z. P. and Shen, J. H.. New solitary wave solutions in a perturbed generalized BBM equation. Nonlinear Dyn. 97 (2019), 2413–2423.CrossRefGoogle Scholar