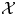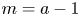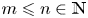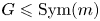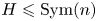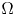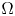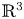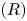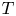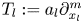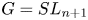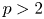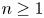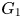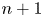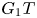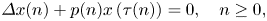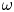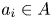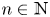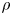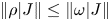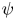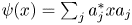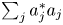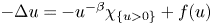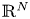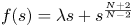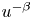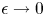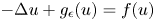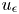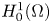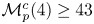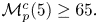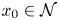Research Article
On birationally trivial families and adjoint quadrics
- Part of:
-
- Published online by Cambridge University Press:
- 04 July 2022, pp. 587-617
-
- Article
- Export citation
The Halász–Székely barycenter
- Part of:
-
- Published online by Cambridge University Press:
- 13 October 2022, pp. 881-911
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some embeddings between symmetric R. thompson groups
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2021, pp. 1-18
-
- Article
- Export citation
On the derivative of a polynomial
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2022, pp. 303-310
-
- Article
- Export citation
Approximation numbers of composition operators on weighted besov spaces of analytic functions
- Part of:
-
- Published online by Cambridge University Press:
- 28 February 2022, pp. 311-325
-
- Article
- Export citation
Fractional powers of higher-order vector operators on bounded and unbounded domains
- Part of:
-
- Published online by Cambridge University Press:
- 13 October 2022, pp. 912-937
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Explicit calculations in an infinitesimal singular block of SLn
- Part of:
-
- Published online by Cambridge University Press:
- 10 February 2022, pp. 19-52
-
- Article
- Export citation
Upper and lower limit oscillation conditions for first-order difference equations
- Part of:
-
- Published online by Cambridge University Press:
- 07 July 2022, pp. 618-631
-
- Article
- Export citation
Intersection of parabolic subgroups in even Artin groups of FC-type
- Part of:
-
- Published online by Cambridge University Press:
- 18 October 2022, pp. 938-957
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized Bloch type periodicity and applications to semi-linear differential equations in banach spaces
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2022, pp. 326-355
-
- Article
- Export citation
Exact solutions and critical behaviour for a linear growth-diffusion equation on a time-dependent domain
- Part of:
-
- Published online by Cambridge University Press:
- 07 December 2021, pp. 53-79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Which states can be reached from a given state by unital completely positive maps?
- Part of:
-
- Published online by Cambridge University Press:
- 05 July 2022, pp. 632-651
-
- Article
- Export citation
Singular elliptic equations with nonlinearities of subcritical and critical growth
- Part of:
-
- Published online by Cambridge University Press:
- 27 July 2022, pp. 652-690
-
- Article
- Export citation
Polynomial null solutions to bosonic Laplacians, bosonic Bergman and Hardy spaces
- Part of:
-
- Published online by Cambridge University Press:
- 13 October 2022, pp. 958-989
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A criterion for normality of analytic mappings
- Part of:
-
- Published online by Cambridge University Press:
- 19 November 2021, pp. 80-88
-
- Article
- Export citation
The local cyclicity problem: Melnikov method using Lyapunov constants
- Part of:
-
- Published online by Cambridge University Press:
- 19 April 2022, pp. 356-375
-
- Article
- Export citation
On free subalgebras of varieties
- Part of:
-
- Published online by Cambridge University Press:
- 22 November 2021, pp. 89-101
-
- Article
- Export citation
On the analyticity of WLUD∞ functions of one variable and WLUD∞ functions of several variables in a complete non-Archimedean valued field
- Part of:
-
- Published online by Cambridge University Press:
- 07 July 2022, pp. 691-704
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Toward a classification of the supercharacter theories of Cp × Cp
- Part of:
-
- Published online by Cambridge University Press:
- 12 October 2022, pp. 990-1010
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A pinching estimate for convex hypersurfaces evolving under a non-homogeneous variant of mean curvature flow
- Part of:
-
- Published online by Cambridge University Press:
- 18 April 2022, pp. 376-391
-
- Article
- Export citation