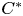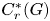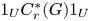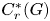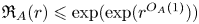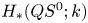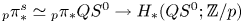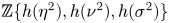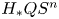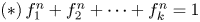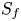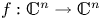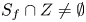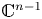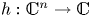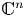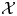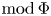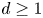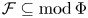Research Article
On semidirectly closed non-aperiodic pseudovarieties of finite monoids
- Part of:
-
- Published online by Cambridge University Press:
- 24 August 2020, pp. 913-928
-
- Article
- Export citation
Dense subalgebras of purely infinite simple groupoid C*-algebras
- Part of:
-
- Published online by Cambridge University Press:
- 30 March 2020, pp. 609-629
-
- Article
- Export citation
The BNSR-invariants of the Houghton groups, concluded
- Part of:
-
- Published online by Cambridge University Press:
- 15 July 2019, pp. 1-11
-
- Article
- Export citation
Virtually spinning hyperbolic manifolds
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2019, pp. 305-313
-
- Article
- Export citation
Bootstrapping partition regularity of linear systems
- Part of:
-
- Published online by Cambridge University Press:
- 09 March 2020, pp. 630-653
-
- Article
- Export citation
Some remarks on the volume of log varieties
- Part of:
-
- Published online by Cambridge University Press:
- 18 December 2019, pp. 314-322
-
- Article
- Export citation
Two boundedness criteria for a class of operators on Musielak–Orlicz Hardy spaces and applications
- Part of:
-
- Published online by Cambridge University Press:
- 16 July 2019, pp. 13-35
-
- Article
- Export citation
Codimension growth for weak polynomial identities, and non-integrality of the PI exponent
- Part of:
-
- Published online by Cambridge University Press:
- 20 July 2020, pp. 929-949
-
- Article
- Export citation
τ-Tilting finite cluster-tilted algebras
- Part of:
-
- Published online by Cambridge University Press:
- 21 July 2020, pp. 950-955
-
- Article
- Export citation
Freudenthal's theorem and spherical classes in H*QS0
- Part of:
-
- Published online by Cambridge University Press:
- 20 December 2019, pp. 323-341
-
- Article
- Export citation
Koszul A∞-algebras and free loop space homology
- Part of:
-
- Published online by Cambridge University Press:
- 18 July 2019, pp. 37-65
-
- Article
- Export citation
Restrictions on meromorphic solutions of Fermat type equations
- Part of:
-
- Published online by Cambridge University Press:
- 08 May 2020, pp. 654-665
-
- Article
- Export citation
On topological approaches to the Jacobian conjecture in ℂn
- Part of:
-
- Published online by Cambridge University Press:
- 07 May 2020, pp. 666-675
-
- Article
- Export citation
d-Auslander–Reiten sequences in subcategories
- Part of:
-
- Published online by Cambridge University Press:
- 15 January 2020, pp. 342-373
-
- Article
- Export citation
Balanced pairs, cotorsion triplets and quiver representations
- Part of:
-
- Published online by Cambridge University Press:
- 13 August 2019, pp. 67-90
-
- Article
- Export citation
A class of simple non-weight modules over the virasoro algebra
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2020, pp. 956-970
-
- Article
- Export citation
Equality case for an elliptic area condenser inequality and a related Schwarz type lemma
- Part of:
-
- Published online by Cambridge University Press:
- 19 August 2019, pp. 91-104
-
- Article
- Export citation
One-generator braces and indecomposable set-theoretic solutions to the Yang–Baxter equation
- Part of:
-
- Published online by Cambridge University Press:
- 06 May 2020, pp. 676-696
-
- Article
- Export citation
Continuous flows generate few homeomorphisms
- Part of:
-
- Published online by Cambridge University Press:
- 25 August 2020, pp. 971-983
-
- Article
- Export citation
Hypergeometric rational approximations to ζ(4)
- Part of:
-
- Published online by Cambridge University Press:
- 03 February 2020, pp. 374-397
-
- Article
-
- You have access
- Open access
- Export citation