Research Article
A special net of quadrics
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 185-209
-
- Article
-
- You have access
- Export citation
On Vanishing Coaxial Minors
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 210-217
-
- Article
-
- You have access
- Export citation
On the Summability of Series by a Method of Valiron
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 218-223
-
- Article
-
- You have access
- Export citation
On the Equivalence of Two Singular Matrix Pencils
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 224-231
-
- Article
-
- You have access
- Export citation
Some new operational representations
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 232-237
-
- Article
-
- You have access
- Export citation
The Boltzmann Equations in General Relativity
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 238-253
-
- Article
-
- You have access
- Export citation
The asymptotic periods of integral and meromorphic functions
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 254-257
-
- Article
-
- You have access
- Export citation
A Geometrical Interpretation of the Symmetrical Invariant of Three Ternary Quadratics
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 258-261
-
- Article
-
- You have access
- Export citation
A Theorem on Alternants
-
- Published online by Cambridge University Press:
- 20 January 2009, p. 261
-
- Article
-
- You have access
- Export citation
Obituary
Sir Thomas Muir, C.M.G., LL.D., F.R.S.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 263-267
-
- Article
-
- You have access
- Export citation
Bertram Martin Wilson, M.A., D.SC, F.R.S.E.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 268-269
-
- Article
-
- You have access
- Export citation
John Edward Aloysius Steggall M.A., LL.D., HON.A.R.I.B.A.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 270-271
-
- Article
-
- You have access
- Export citation
Ellice Martin Horsburgh M.A., D.SC., A.M.INST.C.E., F.R.S.E.
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 272-273
-
- Article
-
- You have access
- Export citation
Index to papers
Index of Papers Published in this Volume Arranged According to Names of Authors
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 275-276
-
- Article
-
- You have access
- Export citation
Index according to subjects
Index According to Subjects
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 276-278
-
- Article
-
- You have access
- Export citation
List of members
List of Members—January 1936
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. 279-286
-
- Article
-
- You have access
- Export citation
Front matter
PEM volume 4 issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back matter
PEM volume 4 issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 20 January 2009, pp. b1-b2
-
- Article
-
- You have access
- Export citation

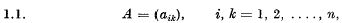
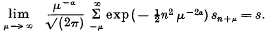
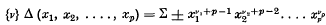
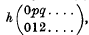 and let {λ} be an
and let {λ} be an