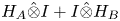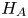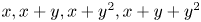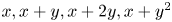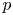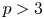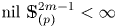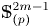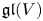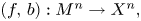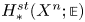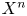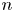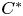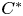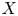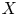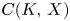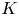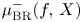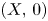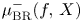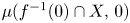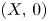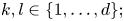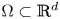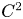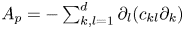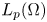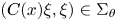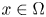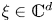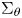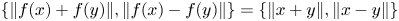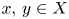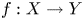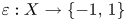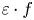Research Article
Self-adjoint extensions of bipartite Hamiltonians
- Part of:
-
- Published online by Cambridge University Press:
- 22 June 2021, pp. 433-447
-
- Article
- Export citation
True complexity of polynomial progressions in finite fields
- Part of:
-
- Published online by Cambridge University Press:
- 07 June 2021, pp. 448-500
-
- Article
- Export citation
Homotopy nilpotency of localized spheres and projective spaces
- Part of:
-
- Published online by Cambridge University Press:
- 04 June 2021, pp. 501-512
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chaos and frequent hypercyclicity for composition operators
- Part of:
-
- Published online by Cambridge University Press:
- 04 June 2021, pp. 513-531
-
- Article
- Export citation
Smooth parameterizations of power-subanalytic sets and compositions of Gevrey functions
- Part of:
-
- Published online by Cambridge University Press:
- 04 June 2021, pp. 532-554
-
- Article
- Export citation
Algebras with representable representations
- Part of:
-
- Published online by Cambridge University Press:
- 24 June 2021, pp. 555-573
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized manifolds, normal invariants, and 𝕃-homology
- Part of:
-
- Published online by Cambridge University Press:
- 16 June 2021, pp. 574-589
-
- Article
- Export citation
On class 2 quotients of linear groups
- Part of:
-
- Published online by Cambridge University Press:
- 09 June 2021, pp. 590-593
-
- Article
- Export citation
Operator equalities and Characterizations of Orthogonality in Pre-Hilbert C*-Modules
- Part of:
-
- Published online by Cambridge University Press:
- 17 June 2021, pp. 594-614
-
- Article
- Export citation
An example regarding Kalton's paper ‘isomorphisms between spaces of vector-valued continuous functions’
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2021, pp. 615-619
-
- Article
- Export citation
Orderability of link quandles
- Part of:
-
- Published online by Cambridge University Press:
- 16 August 2021, pp. 620-649
-
- Article
- Export citation
Computing the fundamental group of a higher-rank graph
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2021, pp. 650-661
-
- Article
- Export citation
The relative Bruce–Roberts number of a function on a hypersurface
- Part of:
-
- Published online by Cambridge University Press:
- 19 August 2021, pp. 662-674
-
- Article
- Export citation
Positive solutions for a degenerate Kirchhoff problem
- Part of:
-
- Published online by Cambridge University Press:
- 19 August 2021, pp. 675-688
-
- Article
- Export citation
On sectoriality of degenerate elliptic operators
- Part of:
-
- Published online by Cambridge University Press:
- 18 August 2021, pp. 689-710
-
- Article
- Export citation
A generalized Davenport expansion
- Part of:
-
- Published online by Cambridge University Press:
- 26 August 2021, pp. 711-715
-
- Article
- Export citation
Retraction
The wigner property for CL-spaces and finite-dimensional polyhedral banach spaces – RETRACTION
-
- Published online by Cambridge University Press:
- 25 October 2021, p. 716
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Research Article
RETRACTED – The wigner property for CL-spaces and finite-dimensional polyhedral banach spaces
- Part of:
-
- Published online by Cambridge University Press:
- 04 June 2021, pp. 717-733
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PEM series 2 volume 64 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 25 October 2021, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PEM series 2 volume 64 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 25 October 2021, pp. b1-b2
-
- Article
-
- You have access
- Export citation