Hostname: page-component-77c89778f8-gq7q9 Total loading time: 0 Render date: 2024-07-17T01:07:41.839Z Has data issue: false hasContentIssue false
  • English
  • Français

Some maximal normal subgroups of the modular group

Published online by Cambridge University Press:  20 January 2009

Gareth A. Jones
Gareth A. Jones
Affiliation:
Department of Mathematics, University of Southampton, Southampton SO9 5NH
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For each finite group G, let 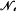G denote the set of all normal subgroups of the modular group Γ = PSL2(ℤ) with quotient group isomorphic to G; since Γ is finitely generated, the number NG = |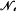G| of such subgroups is finite. We shall be mainly concerned with the case where G is the linear fractional group PSL2(q) over the Galois field GF(q), in which case we shall write 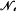(q) and N(q) for 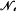G and NG; for q>3, PSL2(q) is simple, so the elements of 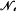(q) will be maximal normal subgroups of Γ.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 30 , Issue 1 , February 1987 , pp. 97 - 101
Copyright
Copyright © Edinburgh Mathematical Society 1987

References

REFERENCES

1.Dickson, L. E., Linear groups (Teubner, Leipzig, 1901 ; reprinted Dover, New York, 1958).Google Scholar
2.Hall, P., The Eulerian functions of a group, Quarterly J. Math. Oxford 1 (1936), 134–151.CrossRefGoogle Scholar
3.Jones, G. A., Triangular maps and non-congruence subgroups of the modular group, Bull. London Math. Soc. 11 (1979), 117–123.CrossRefGoogle Scholar
4.Jones, G. A. and Singerman, D., Theory of maps on orientable surfaces, Proc. London Math. Soc. (3) 37 (1978), 273–307.Google Scholar
5.Macbeath, A. M., Generators of the linear fractional groups, Proc. Sympos. Pure Math. vol. 12 (Amer. Math. Soc, Providence, R.I., 1967), 14–32.Google Scholar
6.Mcquillan, D. L., Classification of normal congruence subgroups of the modular group, Amer. J. Math. 87 (1965), 285–296.Google Scholar
7.Newman, M., Maximal normal subgroups of the modular group, Proc. Amer. Math. Soc. 19 (1968), 1138–1144.Google Scholar
8.Newman, M., Integral matrices (Academic Press, New York, 1972).Google Scholar
9.Sinkov, A., The number of abstract definitions of LF(2, p) as a quotient group of (2, 3, n), J. Algebra 12 (1969), 525–532.Google Scholar