Article contents
On the blow-up and positive entire solutions of semilinear elliptic equations
Published online by Cambridge University Press: 20 January 2009
Abstract
In this paper we consider the following semilinear elliptic equation
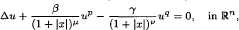
where n ≥ 3, 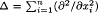 and β ≥ 0, γ ≥ 0, q > p ≥ 1, μ and ν are real constants. We note that if γ = 0, β > 0 and ν ≥ 2, then the equation above is called the Matukuma-type equation. If β = 0, γ > 0 and ν > 2, then the complete classification of all possible positive solutions had been conducted by Cheng and Ni. If β > 0, γ > 0 and μ ≥ ν ≥ 2, then some results about the maximal solution and positive solution structures can be found in Chern. The purpose of this paper is to discuss and investigate the blow-up and positive entire solutions of the equation above for the μ ≥ 2 ≥ ν case.
and β ≥ 0, γ ≥ 0, q > p ≥ 1, μ and ν are real constants. We note that if γ = 0, β > 0 and ν ≥ 2, then the equation above is called the Matukuma-type equation. If β = 0, γ > 0 and ν > 2, then the complete classification of all possible positive solutions had been conducted by Cheng and Ni. If β > 0, γ > 0 and μ ≥ ν ≥ 2, then some results about the maximal solution and positive solution structures can be found in Chern. The purpose of this paper is to discuss and investigate the blow-up and positive entire solutions of the equation above for the μ ≥ 2 ≥ ν case.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 43 , Issue 3 , October 2000 , pp. 625 - 631
- Copyright
- Copyright © Edinburgh Mathematical Society 2000
References
- 1
- Cited by




