Hostname: page-component-848d4c4894-pjpqr Total loading time: 0 Render date: 2024-06-29T10:28:28.942Z Has data issue: false hasContentIssue false
  • English
  • Français

On one-dimensional local rings and Berger’s conjecture

Part of: Local rings and semilocal rings Differential algebra Curves

Published online by Cambridge University Press:  23 May 2023

Cleto B. Miranda-Neto Open the ORCID record for Cleto B. Miranda-Neto [Opens in a new window]
Cleto B. Miranda-Neto*
Affiliation:
Departamento de Matemática, Universidade Federal da Paraíba, João Pessoa, PB, Brazil (cleto@mat.ufpb.br)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let k be a field of characteristic zero and let 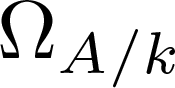$\Omega_{A/k}$ be the universally finite differential module of a k-algebra A, which is the local ring of a closed point of an algebraic or algebroid curve over k. A notorious open problem, known as Berger’s Conjecture, predicts that A must be regular if 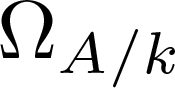$\Omega_{A/k}$ is torsion-free. In this paper, assuming the hypotheses of the conjecture and observing that the module 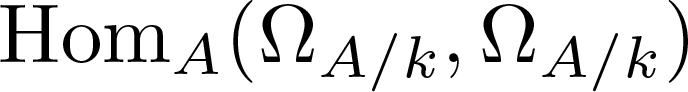${\rm Hom}_A(\Omega_{A/k}, \Omega_{A/k})$ is then isomorphic to an ideal of A, say 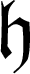$\mathfrak{h}$, we show that A is regular whenever the ring 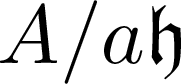$A/a\mathfrak{h}$ is Gorenstein for some parameter a (and conversely). In addition, we provide various characterizations for the regularity of A in the context of the conjecture.

Keywords

module of differentialsone-dimensional regular local ringBerger’s Conjecturealgebraic and algebroid curveshomological characterizations of regularity

MSC classification

Primary: 13N05: Modules of differentials 13H05: Regular local rings
Secondary: 14H20: Singularities, local rings
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 66 , Issue 2 , May 2023 , pp. 437 - 452
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Barucci, V., D’Anna, M. and Strazzanti, F., A family of quotients of the Rees algebra, Comm. Algebra 43 (2015), 130–142.10.1080/00927872.2014.897549CrossRefGoogle Scholar
Bassein, R., On smoothable curve singularities: local methods, Math. Ann. 230 (1977), 273–277.10.1007/BF01367580CrossRefGoogle Scholar
Berger, R., Differentialmoduln eindimensionaler lokaler Ringe, Math. Z. 81 (1963), 326–354.10.1007/BF01111579CrossRefGoogle Scholar
Berger, R., On the torsion of the differential module of a curve singularity, Arch. Math. 50 (1988), 526–533.10.1007/BF01193622CrossRefGoogle Scholar
Berger, R., Report on the torsion of the differential module of an algebraic curve, in Algebraic geometry and its applications, pp. 285–303 (Springer, New York, 1994).10.1007/978-1-4612-2628-4_17CrossRefGoogle Scholar
Bruns, W. and Herzog, J., Cohen–Macaulay rings, Cambridge Studies in Advanced Mathematics, Revised Edition, Volume 39 (Cambridge University Press, 1998).10.1017/CBO9780511608681CrossRefGoogle Scholar
Buchweitz, R.-O. and Greuel, G.-M., The Milnor number and deformations of complex curve singularities, Invent. Math. 58 (1980), 241–281.10.1007/BF01390254CrossRefGoogle Scholar
Celikbas, O. and Takahashi, R., Powers of the maximal ideal and vanishing of (co)homology, Glasg. Math. J. 63 (2021), 1–5.10.1017/S0017089519000466CrossRefGoogle Scholar
Constapel, P., Vanishing of Tor and torsion in tensor products, Comm. Algebra 24 (1996), 833–846.10.1080/00927879608825604CrossRefGoogle Scholar
Cortiñas, G. and Krongold, F., Artinian algebras and differential forms, Comm. Algebra 27 (1999), 1711–1716.10.1080/00927879908826523CrossRefGoogle Scholar
Cortiñas, G., Geller, S. C. and Weibel, C. A., The Artinian Berger conjecture, Math. Z. 228 (1998), 569–588.10.1007/PL00004634CrossRefGoogle Scholar
Dao, H., De Stefani, A., Grifo, E., Huneke, C. and Núñez-Betancourt, L., Symbolic powers of ideals, in Springer Proceedings in Mathematics & Statistics, Volume 222, pp. 387–432 (Springer, Cham, 2018).Google Scholar
Elias, J., On the canonical ideals of one-dimensional Cohen–Macaulay local rings, Proc. Edinb. Math. Soc. 59 (2016), 77–90.10.1017/S0013091514000418CrossRefGoogle Scholar
Ghosh, D. and Takahashi, R., Auslander–Reiten conjecture and finite injective dimension of Hom, available at https://arxiv.org/abs/2109.00692v2, 2023.Google Scholar
Güttes, K., Zum Torsionsproblem bei Kurvensingularitäten, Arch. Math. 54 (1990), 499–510.10.1007/BF01188678CrossRefGoogle Scholar
Hanes, D. and Huneke, C., Some criteria for the Gorenstein property, J. Pure Appl. Algebra 201 (2005), 4–16.10.1016/j.jpaa.2004.12.038CrossRefGoogle Scholar
Herzog, J., Ein Cohen–Macaulay Kriterium mit Anwendungen auf den Konormalenmodul und den Differentialmodul, Math. Z. 163 (1978), 149–162.10.1007/BF01214062CrossRefGoogle Scholar
Herzog, J., Eindimensionale fast-vollständige Durchschnitte sind nicht starr, Manuscripta Math. 30 (1979), 1–19.10.1007/BF01305988CrossRefGoogle Scholar
Herzog, J., The module of differentials, Lecture notes, Workshop on Commmutative Algebra and its Relation to Combinatorics and Computer Algebra, International Centre for Theoretical Physics, (Trieste, Italy, 1994).Google Scholar
Herzog, J. and Waldi, R., A note on the Hilbert function of a one-dimensional Cohen–Macaulay ring, Manuscripta Math. 16 (1975), 251–260.10.1007/BF01164427CrossRefGoogle Scholar
Herzog, J. and Waldi, R., Differentials of linked curve singularities, Arch. Math. 42 (1984), 335–343.10.1007/BF01246124CrossRefGoogle Scholar
Herzog, J. and Waldi, R., Cotangent functors of curve singularities, Manuscripta Math. 55 (1986), 307–34l.10.1007/BF01186649CrossRefGoogle Scholar
Huneke, C., Ideals defining Gorenstein rings are (almost) never products, Proc. Amer. Math. Soc. 135 (2007), 2003–2005.10.1090/S0002-9939-07-08758-8CrossRefGoogle Scholar
Huneke, C. and Swanson, I., Integral closure of ideals Rings and modules, London Mathematical Society Lecture Note Series, Volume 336 (Cambridge University Press, 2006).Google Scholar
Huneke, C., Iyengar, S. B. and Wiegand, R., Rigid ideals in Gorenstein rings of dimension one, Acta Math. Vietnam. 44 (2019), 31–49.10.1007/s40306-018-00315-0CrossRefGoogle Scholar
Isogawa, S., On Berger’s conjecture about one dimensional local rings, Arch. Math. 57 (1991), 432–437.10.1007/BF01246739CrossRefGoogle Scholar
Kunz, E., Kähler differentials, Advanced Lectures in Mathematics (Vieweg, 1986).10.1007/978-3-663-14074-0CrossRefGoogle Scholar
Pohl, T., Differential modules with maximal torsion, Arch. Math. 57 (1991), 438–445.10.1007/BF01246740CrossRefGoogle Scholar
Scheja, G., Differentialmoduln lokaler analytischer Algebren, Schriftenreihe Math. Inst. Univ. Fribourg, No. 2 (Univ. Fribourg, Switzerland, 1969/70).Google Scholar
Schenzel, P. and Simon, A.-M., Completion, Čech and local homology and cohomology interactions between them, Springer Monographs in Mathematics (Springer, Cham, 2018).10.1007/978-3-319-96517-8CrossRefGoogle Scholar
Ulrich, B., Torsion des Differentialmoduls und Kotangentenmodul von Kurvensingularitäten, Arch. Math. 36 (1981), 510–523.10.1007/BF01223733CrossRefGoogle Scholar
Ulrich, B., Gorenstein rings and modules with high numbers of generators, Math. Z. 188 (1984), 23–32.10.1007/BF01163869CrossRefGoogle Scholar
Vasconcelos, W., Reflexive modules over Gorenstein rings, Proc. Amer. Math. Soc. 19 (1968), 1349–1355.10.1090/S0002-9939-1968-0237480-2CrossRefGoogle Scholar
Zargar, M. R., Celikbas, O., Gheibi, M. and Sadeghi, A., Homological dimensions of rigid modules, Kyoto J. Math. 58 (2018), 639–669.10.1215/21562261-2017-0033CrossRefGoogle Scholar