Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T03:46:44.436Z Has data issue: false hasContentIssue false
  • English
  • Français

On asymptotic behaviours of trigonometric series with δ-Quasi-monotone coefficients

Published online by Cambridge University Press:  20 January 2009

Ming-Chit Liu
Ming-Chit Liu
Affiliation:
Department of Mathematics, University of Hong Kong
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let

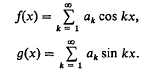
The asymptotic behaviours of ƒ(x) and g(x), as x→+0, were first given by G. H. Hardy in (4), (5). In his papers {an}; is a monotone decreasing sequence. Further results on the asymptotic behaviours of ƒ(x) and g(x), as x→+0, for monotone coefficients have been given in (9) and (1). Recently, the results have been generalized to quasi-monotone coefficients.

This paper is concerned with asymptotic behaviours of ƒ(x) and g(x) for δ-quasi-monotone coefficients.

In what follows, we shall denote by L(x) a slowly varying function in the sense of Karamata (6), i.e.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 16 , Issue 4 , December 1969 , pp. 305 - 316
Copyright
Copyright © Edinburgh Mathematical Society 1969

References

REFERENCES

(1) Aljančić, S., Bojanić, R. et Tomić, M.Sur le comportement asymptotique au voisinage de zéro des séries trigonometriques de sinus á coefficients monotones, Publ. Inst. Math. Acad. Serbe Sci. 10 (1956), 101–20.Google Scholar
(2) AljančIć, S., Bojanić, R. et Ctomić, M., Sur la valeur asymptotique d'une classe des intégrales définies, Publ. Inst. Math. Acad. Serbe Sci. 7 (1954), 81–84.Google Scholar
(3) Boas, R. P.Quasi-positive sequences and trigonometric series, Proc. London Math. Soc. (3) 14A (1965), 38–46.Google Scholar
(4) Hardy, G. H.A theorem concerning trigonometrical series, J. London Math. Soc. 3 (1928), 12–13.Google Scholar
(5) Hardy, G. H.Some theorems concerning trigonometrical series, Proc. London Math. Soc. 32 (1931), 441–8.Google Scholar
(6) Karamata, J.Sur un mode de croissance reguliere des fonctions, Mathematica 4 (1930), 38–53.Google Scholar
(7) Kramata, J.Neuer Beweis und Verallgemeinerung einiger Tauberian-Satze, Math. Zeitschrift, 33 (1931), 294–9.Google Scholar
(8) Karamata, J.Sur un mode de croissance reguliere, Bull. Soc. Math. France, 61 (1933), 55–62.Google Scholar
(9) Zygmund, A.Trigonometric series (2nd ed., Cambridge, 1959), Vol. 1.Google Scholar