No CrossRef data available.
Article contents
Normalized solutions to the quasilinear Schrödinger equations with combined nonlinearities
Part of:
Elliptic equations and systems
Published online by Cambridge University Press: 12 April 2024
Abstract
We consider the radially symmetric positive solutions to quasilinear problem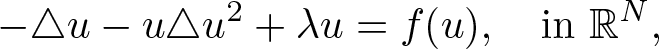
\begin{equation*}-\triangle u-u\triangle u^{2}+\lambda u=f(u),\quad{\rm in} \ \mathbb{R}^{N},\end{equation*}
having prescribed mass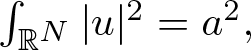 
$\int_{\mathbb{R}^{N}}|u|^2 =a^2,$ where a > 0 is a constant, λ appears as a Lagrange multiplier. We focus on the pure L2-supercritical case and combination case of L2-subcritical and L2-supercritical nonlinearities
\begin{equation*}f(u)=\tau |u|^{q-2}u+|u|^{p-2}u,\quad \tau \gt 0,\qquad{\rm where}\ \ 2 \lt q \lt 2+\frac{4}{N} \ {\rm and} \quad \ p \gt \bar{p},\end{equation*}
where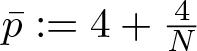 
$\bar{p}:=4+\frac{4}{N}$ is the L2-critical exponent. Our work extends and develops some recent results in the literature.
- Type
- Research Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society.
References
Adachi, S. and Watanabe, T., Uniqueness of ground state solutions for quasilinear Schrödinger equations, Nonl. Anal. 75(2) (2012), 819–833.CrossRefGoogle Scholar
Agueh, M., Sharp Gagliardo–Nirenberg inequalities via p-Laplacian type equations, Nonl. Differ. Equ. Appl. 15 (2008), 457–472.CrossRefGoogle Scholar
Ambrosetti, A., Badiale, M. and Cingolani, S., Semiclassical states of nonlinear Schrödinger equations, Arch. Ration. Mech. Anal. 140 (1997), 285–300.CrossRefGoogle Scholar
Ambrosetti, A. and Wang, Z., Positive solutions to a class of quasilinear elliptic equations on 
$\mathbb{R}$, Discrete Contin. Dyn. Syst. 9 (2003), 55–68.CrossRefGoogle Scholar
$\mathbb{R}$, Discrete Contin. Dyn. Syst. 9 (2003), 55–68.CrossRefGoogle ScholarAo, Y. and Zou, W., Ground states for a class of quasilinear elliptic systems with critical exponent, Nonl. Anal. 181 (2019), 222–248.CrossRefGoogle Scholar
Barstch, T. and Soave, N., Multiple normalized solutions for a competing system of Schrödinger equations, Calc. Var. Partial Differ. Equ. 58 (2019), , doi: 10.1007/s00526-018-1476-x.Google Scholar
Barstch, T. and Wang, Z., Existence and multiplicity results for some superlinear elliptic problems on $\mathbb{R}^N$, Commun. Partial Differ. Equ. 20 (1995), 1725–1741.Google Scholar
$\mathbb{R}^N$, Commun. Partial Differ. Equ. 20 (1995), 1725–1741.Google ScholarBarstch, T., Wang, Z. and Willem, M., The Dirichlet problem for superlinear elliptic equations, In Quittner, P. (Ed), Handbook of Differential Equations-Stationary Partial Differential Equations, Vol. 2 (Elsevier, 2005). doi:10.1016/S1874-5733(05)80009-9Google Scholar
Berestycki, H. and Lions, P.-L., Nonlinear scalar field equations. II: existence of infinitely many solutions, Arch. Rational Mech. Anal. 82 (1983), 347–375.CrossRefGoogle Scholar
Cazenave, T., Semilinear Schrödinger Equations, Vol. 10, Cournant Lecture Notes in Mathematica (New York University, New York, 2003).Google Scholar
Chang, K. C., Methods in Nonlinear Analysis, Springer Monographs in Mathematics (Springer-Verlag, Berlin, 2005).Google Scholar
Cingolani, S., Jeanjean, L. and Squassina, M., Stability and instability results for standing waves of quasilinear Schrödinger equations, Nonlinearity 23 (2010), 1353–1385.Google Scholar
Colin, M. and Jeanjean, L., Solutions for quasilinear Schrödinger equation: a dual approach, Nonl. Anal. 56 (2004), 213–226.CrossRefGoogle Scholar
Colin, M., Jeanjean, L. and Squassina, M., Stability and instability results for standing waves of quasi-linear Schrödinger equations, Nonlinearity 23 (2010), 1353–1385.CrossRefGoogle Scholar
Fang, X. and Szulkin, A., Multiple solutions for a quasilinear Schrödinger equation, J. Differ. Equ. 254 (2013), 2015–2032.CrossRefGoogle Scholar
Gladiali, F. and Squassina, M., Uniqueness of ground states for a class of quasilinear elliptic equations, Adv. Nonl. Anal. 1 (2012), 159–179.Google Scholar
Ghoussoub, N., Duality and Perturbation Methods in Critical Point Theory, Vol. 1.7, Cambridge Tracts in Mathematics (Cambridge University Press, Cambridge, 1993), with appendices by Daid Robinson.CrossRefGoogle Scholar
Jeanjean, L., Existence of solutions with prescribed norm for semilinear elliptic equations, Nonl. Anal. 28 (1997), 1633–1659.CrossRefGoogle Scholar
Jeanjean, L., Le, T. and Wang, Z., Multiple normalized solutions for quasilinear Schrödinger equation, J. Differ. Equ. 259 (2015), 3894–3928.CrossRefGoogle Scholar
Jeanjean, L. and Luo, T., Sharp non-existence results of prescribed L 2-norm solutions for some class of Schrödinger-Poisson and quasi-linear equations, Z. Angew. Math. Phys. 64 (2013), 937–954.CrossRefGoogle Scholar
Kurihura, S., Large-amplitude quasi-solitions in superfluid films, J. Phys. Soc. Jpn. 50 (1981), 3262–3267.CrossRefGoogle Scholar
Lieb, E. H. and Loss, M., Analysis, 2nd edn. (American Mathematical Society, Providence, RI, 2001).Google Scholar
Li, H. and Zou, W., Quasilinear Schrödinger equations: ground state and infinitely many normalized solutions, Pac. J. Math. 322 (2023), 99–138.CrossRefGoogle Scholar
Li, Q., Wang, W., Teng, K. and Wu, X., Multiple solutions for a class of quasilinear Schrödinger equation, Math. Nachr. 292 (2019), 1530–1550.CrossRefGoogle Scholar
Liu, J., Wang, Y. and Wang, Z., Soliton solutions for quasilinear Schrödinger equations II, J. Differ. Equ. 187 (2003), 473–493.CrossRefGoogle Scholar
Liu, J., Wang, Y. and Wang, Z., Solutions for quasilinear Schrödinger equations via Nehari method, Commun. Partial Differ. Equ. 29 (2004), 879–901.CrossRefGoogle Scholar
Liu, J. and Wang, Z., Multiple solutions for quasilinear elliptic equations with a finite potential well, J. Differ. Equ. 257 (2014), 2874–2899.CrossRefGoogle Scholar
Liu, X., Liu, J. and Wang, Z., Quasilinear elliptic equations via perturbation method, Proc. Amer. Math. Soc. 141 (2013), 253–263.CrossRefGoogle Scholar
Liu, X., Liu, J. and Wang, Z., Quasilinear elliptic equations with critical growth via perturbation method, J. Differ. Equ. 254 (2013), 102–124.CrossRefGoogle Scholar
Poppenberg, M., Schmitt, K. and Wang, Z., On the existence of soliton solutions to quasilinear Schrödinger equations, Calc. Var. Partial Differ. Equ. 14 (2002), 329–344.CrossRefGoogle Scholar
Dong, X. and Mao, A., Existence and multiplicity results for general quasilinear elliptic equations, Siam J. Math. Anal. 53 (2021), 4965–4984.CrossRefGoogle Scholar
Rabinowitz, P., On a class of nonlinear Schrödinger equations, Z. Angew. Math. Phys. 43 (1992), 270–291.CrossRefGoogle Scholar
Ruiz, D. and Siciliano, G., Existence of ground states for a modified nonlinear Schrödinger equation, Nonlinearity 23 (2010), 1221–1233.CrossRefGoogle Scholar
Selvitella, A., Uniqueness and nondegeneracy of the ground state for a quasilinear Schrödinger equation with a small parameter, Nonl. Anal. 74 (2011), 1731–1737.CrossRefGoogle Scholar
Serrin, J. and Tang, M., Uniqueness of ground states for quasilinear elliptic equations, Indiana Univ. Math. J. 49 (2000), 897–923.CrossRefGoogle Scholar
Soave, N., Normalized ground states for the NLS equation with combined nonlinearities, J. Differ. Equ. 269 (2020), 6941–6987.CrossRefGoogle Scholar
Soave, N., Normalized ground states for the NLS equation with combined nonlinearities: the Sobolev critical case, J. Funct. Anal. 279 (2020), .CrossRefGoogle Scholar
Talenti, G., Best constant in Sobolev inequality, Ann. Mat. Pura Appl. 110 (1976), 353–372.CrossRefGoogle Scholar
Tang, X., Infinitely many solutions for semilinear Schrödinger equations with sign-changing potential and nonlinearity, J. Math. Anal. Appl. 401 (2013), 407–415.CrossRefGoogle Scholar
Tang, X., New super-quadratic conditions on ground state solutions for superlinear Schröinger equation, Adv. Nonl. Stud. 14 (2014), 349–361.Google Scholar
Tarantello, G., On nonhomogeneous elliptic equations involving critical Sobolev exponent, Ann. Inst. H. Poincaré C 9 (1992), 281–304.CrossRefGoogle Scholar
Wei, J. and Wu, Y., Normalized solutions for Schrödinger equations with critical Sobolev exponent and mixed nonlinearities, J. Funct. Anal. 283 (2022), .CrossRefGoogle Scholar
Weinstein, M., Nonlinear Schrödinger equations and sharp interpolation estimates, Commun. Math. Phys. 87 (1983), 567–576.CrossRefGoogle Scholar
Ye, H. and Yu, Y., The existence of normalized solutions for L 2-critical quasilinear Schrödinger equations, J. Math. Anal. Appl. 497 (2021), .CrossRefGoogle Scholar
Zeng, X. and Zhang, Y., Existence and asymptotic behavior for the ground state of quasilinear elliptic equations, Adv. Nonl. Stud. 18 (2018), 725–744.CrossRefGoogle Scholar
Zhang, J. and Zhao, F., Multiple solutions for a semiclassical Schrödinger equation, Nonl. Anal. 75 (2012), 1834–1842.CrossRefGoogle Scholar