Hostname: page-component-76fb5796d-22dnz Total loading time: 0 Render date: 2024-04-27T02:42:31.585Z Has data issue: false hasContentIssue false
  • English
  • Français

Limiting cases of Boardman's five halves theorem

Part of: Differential topology

Published online by Cambridge University Press:  28 June 2013

Michael C. Crabb  and
Pedro L. Q. Pergher
Michael C. Crabb
Affiliation:
Institute of Mathematics, University of Aberdeen, Aberdeen AB24 3UE, UK (m.crabb@abdn.ac.uk)
Pedro L. Q. Pergher
Affiliation:
Departamento de Matemática, Universidade Federal de Säo Carlos, Caixa Postal 676, Säo Carlos, SP 13565-905, Brazil (pergher@dm.ufscar.br)
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The famous five halves theorem of Boardman states that, if T: Mm → Mm is a smooth involution defined on a non-bounding closed smooth m-dimensional manifold Mm (m > 1) and if

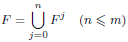
is the fixed-point set of T, where Fj denotes the union of those components of F having dimension j, then 2m ≤ 5n. If the dimension m is written as m = 5k − c, where k ≥ 1 and 0 ≤ c < 5, the theorem states that the dimension n of the fixed submanifold is at least β(m), where β(m) = 2k if c = 0, 1, 2 and β(m) = 2k − 1 if c = 3, 4. In this paper, we give, for each m > 1, the equivariant cobordism classification of involutions (Mm, T), for which the fixed submanifold F attains the minimal dimension β(m).

Keywords

five halves theoreminvolutionfixed-point dataequivariant cobordism classStiefel–Whitney classcharacteristic number

MSC classification

Secondary: 57R85: Equivariant cobordism 57R75: ${rm O}$- and ${rm SO}$-cobordism
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 56 , Issue 3 , October 2013 , pp. 723 - 732
Copyright
Copyright © Edinburgh Mathematical Society 2013 

References

1.Boardman, J. M., On manifolds with involution, Bull. Am. Math. Soc. 73 (1967), 136–138.CrossRefGoogle Scholar
2.Conner, P. E., Differentiable periodic maps, 2nd edn, Lecture Notes in Mathematics (Springer, 1979).Google Scholar
3.Conner, P. E. and Floyd, E. E., Differentiable periodic maps (Springer, 1964).Google Scholar
4.Kosniowski, C. and Stong, R. E., Involutions and characteristic numbers, Topology 17 (1978), 309–330.CrossRefGoogle Scholar
5.Lü, Z., Involutions fixing ℝℙodd⊔P(h, i), I, Trans. Am. Math. Soc. 354 (2002), 4539–4570.CrossRefGoogle Scholar
6.de Oliveira, R., Pergher, P. L. Q. and Ramos, A., Zk 2-actions fixing ℝP2 ∪ ℝPeven, Alg. Geom. Topol. 7 (2007), 29–45.CrossRefGoogle Scholar
7.Sinha, D., Real equivariant bordism and stable transversality obstructions for ℤ/2, Proc. Am. Math. Soc. 130 (2001), 271–281.CrossRefGoogle Scholar
8.Stong, R. E., Involutions with n-dimensional fixed set, Math. Z. 178 (1981), 443–447.CrossRefGoogle Scholar
9.Thom, R., Quelques propriétés globales des variétés différentiables, Comment. Math. Helv. 28 (1954), 18–88.CrossRefGoogle Scholar
10.Torrence, B. F., Bordism classes of vector bundles over real projective spaces, Proc. Am. Math. Soc. 118 (1993), 963–969.CrossRefGoogle Scholar