Let 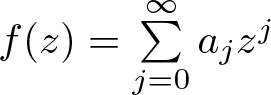$f(z)=\sum\limits_{j=0}^{\infty} a_j z^j$ be a transcendental entire function and let 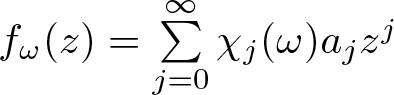$f_\omega(z)=\sum\limits_{j=0}^{\infty}\chi_j(\omega) a_j z^j$ be a random entire function, where 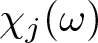$\chi_j(\omega)$ are independent and identically distributed random variables defined on a probability space 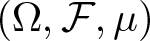$(\Omega, \mathcal{F}, \mu)$. In this paper, we first define a family of random entire functions, which includes Gaussian, Rademacher and Steinhaus entire functions. We prove that, for almost all functions in the family and for any constant C > 1, there exist a constant 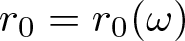$r_0=r_0(\omega)$ and a set 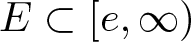$E\subset [e, \infty)$ of finite logarithmic measure such that, for $r \gt r_0$ and 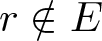$r\notin E$,

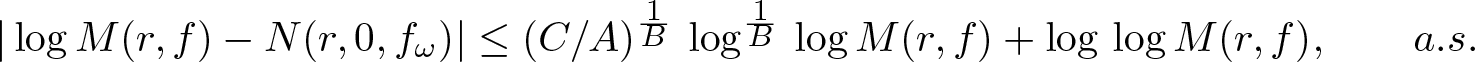\begin{equation*}|\log M(r, f)- N(r,0, f_\omega)|\le (C/A)^{\frac1{B}}\,\log^{\frac1{B}}\,\log M(r,f) +\log\,\log M(r, f), \qquad a.s.\end{equation*}

where 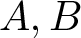$A, B$ are constants, 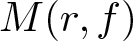$M(r, f)$ is the maximum modulus and 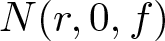$N(r, 0, f)$ is the integrated zero-counting function of f. As a by-product of our main results, we prove Nevanlinna’s second main theorem for random entire functions. Thus, the characteristic function of almost all functions in the family is bounded above by an integrated counting function, rather than by two integrated counting functions as in the classical Nevanlinna theory. For instance, we show that, for almost all Gaussian entire functions fω and for any ϵ > 0, there is r0 such that, for $r \gt r_0$,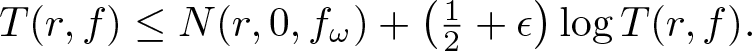

\begin{equation*}T(r, f) \le N(r,0, f_\omega)+\left(\tfrac12+\epsilon\right) \log T(r, f).\end{equation*}