Hostname: page-component-77c89778f8-n9wrp Total loading time: 0 Render date: 2024-07-19T07:48:11.192Z Has data issue: false hasContentIssue false
  • English
  • Français

An Elementary Proof of the Theorems of Cauchy and Mayer

Published online by Cambridge University Press:  20 January 2009

A. J. Macintyre  and
R. Wilson
A. J. Macintyre
Affiliation:
University of Sheffield.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Attention has recently been drawn to the obscurity of the usual presentations of Mayer's method of solution of the total differential equation

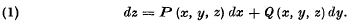
This method has the practical advantage that only a single integration is required, but its theoretical discussion is usually based on the validity of some other method of solution. Mayer's method gives a result even when the equation (1) is not integrable, but this cannot of course be a solution. An examination of the conditions under which the result is actually an integral of equation (1) leads to a proof of the existence theorem for (1) which is related to Mayer's method of solution in a natural way, and which moreover appears to be novel and of value in the presentation of the subject.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 4 , Issue 3 , August 1935 , pp. 112 - 117
Copyright
Copyright © Edinburgh Mathematical Society 1935

References

REFERENCES

1.Carfwright, M. L., Math. Gazette, XVIII (1934), 105–107.CrossRefGoogle Scholar
2.CfGoursat-Hedrick, , Mathematical Analysis, Vol. II, part II (1917), p. 229, §79.Google Scholar
3. This argument is strongly suggested by the concluding remarks of § 152, p. 318Google Scholar
in Goursat-Hedrick, , A Course of Mathematical Analysis, Vol. I (1904), but does not seem to have been pursued. The remark is not to be found in French editions of Goursat's Gours d'Analyse.Google Scholar
4.Goursat-Hedrick, , Vol. I, §97, pp. 192–3 (1904).Google Scholar
5.Cauchy, , Œuvres (1), 10, 70–74, uses Green's Theorem with the same conditions. B. Goursat, Trans. Amer. Math. Soc., 1 (1900), 14, and subsequent writers have shown that continuity is not an independent assumption.Google Scholar
6.Goursat-Hedrick II, II, pp. 61–64. If P (x, y, z) and Q (x, y, z) are continuous and bounded by | x | <a1 | y | <b and | z | <c satisfy a Lipschitz condition with respect to z, then the function f(z, t)=xP(xt, yt, z) + yQ(xt, yt, z) is continuous for these values of x, y, z, and for | t | ≤ 1, and is bounded by M( | x | + | y | ). f(z, t) also satisfies the Lipschitz condition with respect to z. The solution of the differential equation dz/dt = f(z, t) which reduces to z0 for t = t 0 hence exists if hence certainly for | t | ≤1 if | x | and | y | are both less than .Google Scholar
7. That F(x, y, z0, t) has continuous partial derivatives and that the following formal transformations are valid follows from the theory of ordinary differential equations involving parameters.Google Scholar
See de la Poussin, Vallée, Cours d' Analyse, 5th ed. (1925), Vol. II, Ch. 5, §5, 133°, pp. 147–149, and in particular p. 148, 2°. The conditions required are that P(x, y, z) and Q(x, y, z) have continuous derivatives of the first order.Google Scholar
8.Or we may observe that the general solution of (15) is where c is an arbitrary constant and λ – tP must vanish identically or not at all.Google Scholar
9. The Lipschitz condition required for the solution of equation (8) (see Note 6 above) is satisfied on account of the conditions that Pz and Qz are continuous.Google Scholar