Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-01T02:12:50.870Z Has data issue: false hasContentIssue false
  • English
  • Français

On sectoriality of degenerate elliptic operators

Part of: Elliptic equations and systems Special classes of linear operators

Published online by Cambridge University Press:  18 August 2021

Tan Duc Do
Tan Duc Do*
Affiliation:
Division of Applied Mathematics, Thu Dau Mot University, Binh Duong Province, Vietnam (doductan@tdmu.edu.vn)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 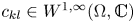$c_{kl} \in W^{1,\infty }(\Omega , \mathbb{C})$ for all 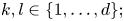$k,l \in \{1, \ldots , d\};$ and 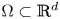$\Omega \subset \mathbb{R}^{d}$ be open with uniformly 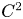$C^{2}$ boundary. We consider the divergence form operator 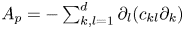$A_p = - \sum \nolimits _{k,l=1}^{d} \partial _l (c_{kl} \partial _k)$ in 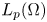$L_p(\Omega )$ when the coefficient matrix satisfies 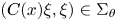$(C(x) \xi , \xi ) \in \Sigma _\theta$ for all 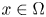$x \in \Omega$ and 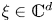$\xi \in \mathbb{C}^{d}$, where 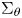$\Sigma _\theta$ be the sector with vertex 0 and semi-angle 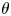$\theta$ in the complex plane. We show that a sectorial estimate holds for 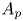$A_p$ for all 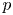$p$ in a suitable range. We then apply these estimates to prove that the closure of 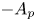$-A_p$ generates a holomorphic semigroup under further assumptions on the coefficients. The contractivity and consistency properties of these holomorphic semigroups are also considered.

Keywords

degenerate elliptic operatorsectorial operatorholomorphic semigroupcontraction semigroupconsistent semigroup

MSC classification

Primary: 35J70: Degenerate elliptic equations 35J15: Second-order elliptic equations
Secondary: 47B44: Accretive operators, dissipative operators, etc.
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 3 , August 2021 , pp. 689 - 710
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Carbonaro, A. and Dragičević, O., Convexity of power functions and bilinear embedding for divergence-form operators with complex coefficients, J. Eur. Math. Soc. 22 (2020), 3175–3221.CrossRefGoogle Scholar
Cialdea, A. and Maz'ya, V., Criterion for the $L^{p}$-dissipativity of second order differential operators with complex coefficients, J. Math. Pures Appl. 84 (2005), 1067–1100.CrossRefGoogle Scholar
Davies, E. B., Heat kernels and spectral theory, Cambridge Tracts in Mathematics, Volume 92 (Cambridge University Press, Cambridge, 1989).CrossRefGoogle Scholar
Do, T. D., Core properties for degenerate elliptic operators with complex bounded coefficients, J. Math. Anal. Appl. 479 (2019), 817–854.10.1016/j.jmaa.2019.06.053CrossRefGoogle Scholar
Do, T. D. and ter Elst, A. F. M., One-dimensional degenerate elliptic operators on $L_p$-spaces with complex coefficients, Semigroup Forum 92 (2016), 559–586.CrossRefGoogle Scholar
Egert, M., On $p$-elliptic divergence form operators and holomorphic semigroups, J. Evol. Equ. 20 (2019), 705–724.CrossRefGoogle Scholar
ter Elst, A. F. M., Haller-Dintelmann, R., Rehberg, J. and Tolksdorf, P., On the $L^{p}$-theory for second-order elliptic operators in divergence form with complex coefficients. arXiv:1903.06692v1.Google Scholar
ter Elst, A. F. M., Liskevich, V., Sobol, Z. and Vogt, H., On the $L^{p}$-theory of $C_0$-semigroups associated with second-order elliptic operators with complex singular coefficients, Proc. London Math. Soc. 115 (2017), 693–724.CrossRefGoogle Scholar
Epperson, J. B., The hypercontractive approach to exactly bounding an operator with complex Gaussian kernel, J. Funct. Anal. 87 (1989), 1–30.CrossRefGoogle Scholar
Goldstein, J. A., Semigroups of linear operators and applications, Oxford Mathematical Monographs (The Clarendon Press, Oxford University Press, New York, 1985).Google Scholar
Kato, T., Perturbation theory for linear operators, 2nd edn. Grundlehren der mathematischen Wissenschaften, Volume 132 (Springer-Verlag, Berlin, 1980).Google Scholar
Liskevich, V. A. and Perelmuter, M. A., Analyticity of sub-Markovian semigroups, Proc. Amer. Math. Soc. 123 (1995), 1097–1104.Google Scholar
Metafune, G. and Spina, C., An integration by parts formula in Sobolev spaces, Mediterr. J. Math. 5 (2008), 357–369.CrossRefGoogle Scholar
Okazawa, N., Sectorialness of second order elliptic operators in divergence form, Proc. Amer. Math. Soc. 113 (1991), 701–706.Google Scholar
Ouhabaz, E.-M., Analysis of heat equations on domains, London Mathematical Society Monographs Series, Volume 31 (Princeton University Press, Princeton, NJ. 2005).Google Scholar
Pazy, A., Semigroups of linear operators and applications to partial differential equations, Applied mathematical sciences, Volume 44 (Springer-Verlag, New York, 1983).CrossRefGoogle Scholar
Reed, M. and Simon, B., Methods of modern mathematical physics II. Fourier analysis, self-adjointness (Academic Press, New York, 1975).Google Scholar
Stein, E. M., Topics in harmonic analysis related to the Littlewood–Paley theory, Annals of Mathematics Studies, Volume 63 (Princeton University Press, Princeton, 1970).Google Scholar
Weissler, F. B., Two-point inequalities, the Hermite semigroup, and the Gauss-Weierstrass semigroup, J. Funct. Anal. 32 (1979), 102–121.CrossRefGoogle Scholar
Wong-Dzung, B., $L^{p}$-Theory of degenerate-elliptic and parabolic operators of second order, Proc. Roy. Soc. Edinburgh Sect. A 95 (1983), 95–113.CrossRefGoogle Scholar