Article contents
PRESERVATION OF LOG-CONCAVITY AND LOG-CONVEXITY UNDER OPERATORS
Published online by Cambridge University Press: 14 February 2020
Abstract
Log-concavity [log-convexity] and their various properties play an increasingly important role in probability, statistics, operations research and other fields. In this paper, we first establish general preservation theorems of log-concavity and log-convexity under operator 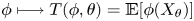 $\phi \longmapsto T(\phi , \theta )=\mathbb {E}[\phi (X_\theta )]$, θ ∈ Θ, where Θ is an interval of real numbers or an interval of integers, and the random variable
$\phi \longmapsto T(\phi , \theta )=\mathbb {E}[\phi (X_\theta )]$, θ ∈ Θ, where Θ is an interval of real numbers or an interval of integers, and the random variable 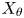 $X_\theta$ has a distribution function belonging to the family
$X_\theta$ has a distribution function belonging to the family 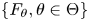 $\{F_\theta , \theta \in \Theta \}$ possessing the semi-group property. The proofs are based on the theory of stochastic comparisons and weighted distributions. The main results are applied to some special operators, for example, operators occurring in reliability, Bernstein-type operators and Beta-type operators. Several known results in the literature are recovered.
$\{F_\theta , \theta \in \Theta \}$ possessing the semi-group property. The proofs are based on the theory of stochastic comparisons and weighted distributions. The main results are applied to some special operators, for example, operators occurring in reliability, Bernstein-type operators and Beta-type operators. Several known results in the literature are recovered.
Keywords
- Type
- Research Article
- Information
- Probability in the Engineering and Informational Sciences , Volume 35 , Issue 3 , July 2021 , pp. 451 - 464
- Copyright
- © Cambridge University Press 2020
References
- 2
- Cited by


