The statistical analysis of networks has become increasingly important in the social and behavioral sciences in recent years. Indeed, inferential and predictive statistical models for networks have been applied to a diverse range of social science problems, including international military alliances (Cranmer, Desmarais, and Menninga Reference Cranmer, Desmarais and Menninga2012), international trade networks (Ward, Ahlquist, and Rozenas Reference Ward, Ahlquist and Rozenas2013), segregation in adolescent friendship networks (Moody Reference Moody2001), communication networks (Eveland and Hively Reference Eveland and Hively2009), social and spatial interaction (Lee, Liu, and Lin Reference Lee, Liu and Lin2010; Gondal Reference Gondal2011), and interest group networks (Box-Steffensmeier and Christenson Reference Box-Steffensmeier and Christenson2014, Reference Box-Steffensmeier and Christenson2015), among many others. These statistical methods are exploding in use as they allow one to relax the conditional independence assumptions required by most other statistical methods. In fact, a key strength of these methods is that they allow complex dependencies—such as reciprocity, homophily, and transitivity—to be explicitly modeled. This allows old theories about social structure and behavior to be analyzed in a new light, while also opening the door for entirely new questions.
Yet, while the statistical analysis of networks continues to attract a great deal of attention from scholars and the broader public, the quantitative study of networks remains in the relatively early stages of development. Only recently have the statistical theory and computational techniques been developed to rigorously analyze many common types of networks, such as weighted and dynamic networks. Moreover, there remains significant gaps in the statistical tools that limit their usefulness to scientists, among the most prevalent of which is the problem of unexplained heterogeneity in models of network formation. Unexplained heterogeneity is simply variation among the nodes that contributes to link formation but goes unmodeled, because it is either unobserved, unmeasured or unimagined.Footnote 1 Our objective is to improve the well-known and widely used exponential random graph model (ERGM), by explicitly modeling unexplained heterogeneity.
The ERGM has been a cornerstone in the revolution of network analysis because it provides a comprehensive and flexible method of incorporating structural network characteristics as well as node and edge traits to explain network formation. However, despite the important advantages of ERGMs over other methods of modeling network data, currently missing is a method of incorporating unobserved heterogeneity into these models. This is an important gap that limits the applicability of ERGMs in many areas of potential interest, given that we expect unobserved heterogeneity to be the rule, rather than the exception. Indeed, one of the two major assumptions of the ERGM is that the model is correctly specified, and coefficient bias or model degeneracy may result from violations of this assumption. In other words, if analysts are unable to collect all the individual-level covariates needed to explicitly model the data generating process, substantive inferences drawn from these models will be suspect. We propose to extend the ERGM to account for this problem through the introduction of a frailty term.
This paper is comprised of three parts. First, we provide a rigorous definition of the proposed frailty ERGM, or FERGM, and compare it to the standard ERGM approach. Second, we perform a series of Monte Carlos to validate the proposed model on networks of various sizes and network characteristics. The objective of the Monte Carlos is to compare the performance of the proposed model to the standard ERGM that does not accommodate unexplained heterogeneity. Beyond the evaluation of the proposed model, the Monte Carlo analysis also provides information about the sensitivity of the standard ERGM to the presence of unexplained heterogeneity. Serious considerations of this nature are absent from the literature and thus this analysis makes a major contribution to the broader literature in its own right.Footnote 2
Third, we demonstrate the applicability and value of the project with applications to two well-known and important social networks: the Lazega (Reference Lazega2001) law firm collaboration network and Magnolia High network (Resnick et al. Reference Resnick, Bearman, Blum, Bauman, Harris, Jones, Tabor, Beuhring, Sieving and Shew1997). These cases serve as critical tests of the FERGM, both because the networks have been explored in depth and because there is good reason to expect different levels of unexplained heterogeneity in the formation of these networks.
This paper also makes an important contribution to the estimation of ERGM-family models by employing a novel multilevel modeling solution. For the undirected networks, we use a multiple-membership mixed-effects model to derive parameter estimates for the network- and node-level network terms included in the model. This estimation strategy has the important advantage of avoiding the vexing problem of degeneration in estimation that plagues the standard MCMC-MLE approach in all but the simplest of networks while, as the Monte Carlo and substantive results show, not greatly affecting the inferences drawn from these models.
1 The ERGM and Frailty Extensions
The ability to include structural and nodal characteristics sets ERGMs apart from other network methods. As a consequence of this flexibility, ERGMs are an attractive modeling option for behavioral, social, natural networks and their coupling (see, e.g., Saul and Filkov Reference Saul and Filkov2007). In this section, we provide a short review of the standard ERGM, along with its limitations, and then present a rigorous description of our proposed extension, the frailty exponential random graph model (FERGM).
1.1 The standard ERGM
Consider a network of
![]() $n$
actors for which some dyadic relationship has been recorded. Such actors may be individuals, groups, or nation-states, while the dyadic relationships may be friendship ties, shared group memberships, bilateral treaties, or other forms of ties between the nodes in the network. In the statistics literature, such relations are usually represented in the form of an adjacency matrix,
$n$
actors for which some dyadic relationship has been recorded. Such actors may be individuals, groups, or nation-states, while the dyadic relationships may be friendship ties, shared group memberships, bilateral treaties, or other forms of ties between the nodes in the network. In the statistics literature, such relations are usually represented in the form of an adjacency matrix,
![]() $Y$
. In the binary networks considered here,Footnote
3
$Y$
. In the binary networks considered here,Footnote
3
![]() $Y$
is an
$Y$
is an
![]() $n\times n$
matrix with each element of the matrix,
$n\times n$
matrix with each element of the matrix,
![]() $y_{ij}\in \{0,\,1\}$
, indicating the existence or absence of a tie between unique actors (nodes)
$y_{ij}\in \{0,\,1\}$
, indicating the existence or absence of a tie between unique actors (nodes)
![]() $i$
and
$i$
and
![]() $j$
in the network. In undirected networks,
$j$
in the network. In undirected networks,
![]() $y_{ij}=y_{ji}\;\forall i\neq j$
; i.e., the adjacency matrix is symmetric. In directed networks, this symmetry does not necessarily hold. In other words, one member of a dyad may “send” a tie to the other member, but not “receive” a reciprocal tie in return.
$y_{ij}=y_{ji}\;\forall i\neq j$
; i.e., the adjacency matrix is symmetric. In directed networks, this symmetry does not necessarily hold. In other words, one member of a dyad may “send” a tie to the other member, but not “receive” a reciprocal tie in return.
The purpose of the ERGM is to model the probability of observing a given network conditional on a set of measures on that network. Mathematically, the ERGM is defined as
Here,
![]() ${\mathcal{Y}}$
is the support of
${\mathcal{Y}}$
is the support of
![]() $y$
,
$y$
,
![]() $\unicode[STIX]{x1D6E4}(y,\mathbf{x})$
is a vector of network statistics calculated on
$\unicode[STIX]{x1D6E4}(y,\mathbf{x})$
is a vector of network statistics calculated on
![]() $y$
and on (exogenous) nodal characteristics
$y$
and on (exogenous) nodal characteristics
![]() $\mathbf{x}$
, and
$\mathbf{x}$
, and
![]() $\unicode[STIX]{x1D703}$
is a vector of model coefficients.
$\unicode[STIX]{x1D703}$
is a vector of model coefficients.
![]() $\unicode[STIX]{x1D6E4}$
can include any number of measures of the structural characteristics of the network, such as measures of density and transitivity. The denominator in (1), abbreviated below by
$\unicode[STIX]{x1D6E4}$
can include any number of measures of the structural characteristics of the network, such as measures of density and transitivity. The denominator in (1), abbreviated below by
![]() $\unicode[STIX]{x1D705}$
, represents all possible networks that could be formed given the fixed set of nodes in the network.
$\unicode[STIX]{x1D705}$
, represents all possible networks that could be formed given the fixed set of nodes in the network.
As Cranmer and Desmarais (Reference Cranmer and Desmarais2011) have recently pointed out, the ERGM is something of a peculiar model when compared to models typically seen in social science. This is the case for a couple reasons. First, unlike the more familiar statistical models, ERGMs operate on a single realization of a network; i.e., they model the probability of observing the given network,
![]() $y$
, with what is essentially a single observation. Second, complex dependencies are allowed in the model. In other words, there is no assumption of independence between observations. These traits are important to fully understand the model and they further highlight the importance of the proposed frailty extension.
$y$
, with what is essentially a single observation. Second, complex dependencies are allowed in the model. In other words, there is no assumption of independence between observations. These traits are important to fully understand the model and they further highlight the importance of the proposed frailty extension.
This family of models has become well utilized in the social sciences, where they are more generally referred to as
![]() $p\ast$
models. While the modern ERGM is largely attributed to Wasserman and Pattison (Reference Wasserman and Pattison1996), the foundations were laid much earlier in spatial statistics (Besag Reference Besag1974), and further developed by work on the network distributions, the class of models, and estimation techniques (Feinberg and Wasserman Reference Feinberg and Wasserman1981; Holland and Leinhardt Reference Holland and Leinhardt1981; Frank and Strauss Reference Frank and Strauss1986). Currently, likelihood-based inference is provided by Markov chain Monte Carlo Maximum Likelihood (MCMC-MLE) algorithms (Corander, Dahmström, and Dahmström Reference Corander, Dahmström and Dahmström1998; Crouch, Wasserman, and Trachtenberg Reference Crouch, Wasserman and Trachtenberg1998; Besag Reference Besag2000; Handcock Reference Handcock2000; Snijders Reference Snijders2002) as well as pseudolikelihood procedures (Strauss and Ikeda Reference Strauss and Ikeda1990; Wasserman and Pattison Reference Wasserman and Pattison1996), though there are important objections to the latter (Besag Reference Besag2000; Snijders Reference Snijders2002). Important to the analysis of social processes, many extensions to the ERGM have allowed for role analysis (Salter-Townshend and Brendan Murphy Reference Salter-Townshend and Brendan Murphy2015) and the consideration of egocentrically sampled network data (Krivitsky, Handcock, and Morris Reference Krivitsky, Handcock and Morris2011). In addition, this family of models is developing to consider longitudinal or dynamic networks in the form of temporal ERGMs (TERGMs) (Hanneke and Xing Reference Hanneke, Xing, Airoldi, Blei, Fienberg, Goldenberg, Xing and Zheng2007; Hanneke, Fu, and Xing Reference Hanneke, Fu and Xing2010; Desmarais and Cranmer Reference Desmarais and Cranmer2010; Cranmer and Desmarais Reference Cranmer and Desmarais2011) and separable temporal ERGMs (STERGMs) (Krivitsky and Handcock Reference Krivitsky and Handcock2014; Christenson and Box-Steffensmeier Reference Christenson, Box-Steffensmeier, Cherifi, Gaito, Quattrociocchi and Sala2016).
$p\ast$
models. While the modern ERGM is largely attributed to Wasserman and Pattison (Reference Wasserman and Pattison1996), the foundations were laid much earlier in spatial statistics (Besag Reference Besag1974), and further developed by work on the network distributions, the class of models, and estimation techniques (Feinberg and Wasserman Reference Feinberg and Wasserman1981; Holland and Leinhardt Reference Holland and Leinhardt1981; Frank and Strauss Reference Frank and Strauss1986). Currently, likelihood-based inference is provided by Markov chain Monte Carlo Maximum Likelihood (MCMC-MLE) algorithms (Corander, Dahmström, and Dahmström Reference Corander, Dahmström and Dahmström1998; Crouch, Wasserman, and Trachtenberg Reference Crouch, Wasserman and Trachtenberg1998; Besag Reference Besag2000; Handcock Reference Handcock2000; Snijders Reference Snijders2002) as well as pseudolikelihood procedures (Strauss and Ikeda Reference Strauss and Ikeda1990; Wasserman and Pattison Reference Wasserman and Pattison1996), though there are important objections to the latter (Besag Reference Besag2000; Snijders Reference Snijders2002). Important to the analysis of social processes, many extensions to the ERGM have allowed for role analysis (Salter-Townshend and Brendan Murphy Reference Salter-Townshend and Brendan Murphy2015) and the consideration of egocentrically sampled network data (Krivitsky, Handcock, and Morris Reference Krivitsky, Handcock and Morris2011). In addition, this family of models is developing to consider longitudinal or dynamic networks in the form of temporal ERGMs (TERGMs) (Hanneke and Xing Reference Hanneke, Xing, Airoldi, Blei, Fienberg, Goldenberg, Xing and Zheng2007; Hanneke, Fu, and Xing Reference Hanneke, Fu and Xing2010; Desmarais and Cranmer Reference Desmarais and Cranmer2010; Cranmer and Desmarais Reference Cranmer and Desmarais2011) and separable temporal ERGMs (STERGMs) (Krivitsky and Handcock Reference Krivitsky and Handcock2014; Christenson and Box-Steffensmeier Reference Christenson, Box-Steffensmeier, Cherifi, Gaito, Quattrociocchi and Sala2016).
As an aside, it is important to recognize that the ERGM is only one of a handful of related models used to understand data with complex interdependencies. The
![]() $p\ast$
model has been extended to identify between- and within-group ties for groups with stochastic block models (Wang and Wong Reference Wang and Wong1987). When group membership is unobserved, Nowicki and Snijders (Reference Nowicki and Snijders2001) provide a model to describe latent class membership. The agent-based approach of Snijders (Reference Snijders2001) posits conditionally independent dyads on latent class membership, which can be used to understand features of social network dynamics (see also Snijders, Van de Bunt, and Steglich Reference Snijders, Van de Bunt and Steglich2010). Relatedly, latent space models, which generally reduce higher-order network dependencies down to lower dimensional spaces, have grown out of work in spatial statistics (Hoff, Raftery, and Handcock Reference Hoff, Raftery and Handcock2002; Hoff and Ward Reference Hoff and Ward2004; Franzese and Hays Reference Franzese and Hays2006), and have paid particular attention to exploring network dynamics. For example, Ward and Hoff (Reference Ward and Hoff2007) model ties at each time period as a function of latent covariates (see also Ward, Ahlquist, and Rozenas Reference Ward, Ahlquist and Rozenas2013; Durante and Dunson Reference Durante and Dunson2014). More recently, Hoff et al. (Reference Hoff2015) provides a method that combines the dependence representation of the agent-based approach with the node heterogeneity of latent space approaches (see also Minhas, Hoff, and Ward Reference Minhas, Hoff and Ward2016).
$p\ast$
model has been extended to identify between- and within-group ties for groups with stochastic block models (Wang and Wong Reference Wang and Wong1987). When group membership is unobserved, Nowicki and Snijders (Reference Nowicki and Snijders2001) provide a model to describe latent class membership. The agent-based approach of Snijders (Reference Snijders2001) posits conditionally independent dyads on latent class membership, which can be used to understand features of social network dynamics (see also Snijders, Van de Bunt, and Steglich Reference Snijders, Van de Bunt and Steglich2010). Relatedly, latent space models, which generally reduce higher-order network dependencies down to lower dimensional spaces, have grown out of work in spatial statistics (Hoff, Raftery, and Handcock Reference Hoff, Raftery and Handcock2002; Hoff and Ward Reference Hoff and Ward2004; Franzese and Hays Reference Franzese and Hays2006), and have paid particular attention to exploring network dynamics. For example, Ward and Hoff (Reference Ward and Hoff2007) model ties at each time period as a function of latent covariates (see also Ward, Ahlquist, and Rozenas Reference Ward, Ahlquist and Rozenas2013; Durante and Dunson Reference Durante and Dunson2014). More recently, Hoff et al. (Reference Hoff2015) provides a method that combines the dependence representation of the agent-based approach with the node heterogeneity of latent space approaches (see also Minhas, Hoff, and Ward Reference Minhas, Hoff and Ward2016).
Our objective in this paper is to improve on the well-used, powerful and flexible ERGM. It is not to argue that the ERGM should be used to model all networks. One or more of the approaches above may be more appropriate for a particular research question or data set.Footnote 4 As stated by Cranmer and Desmarais (Reference Cranmer and Desmarais2011, 68), the best approach for modeling complex interdependencies will be “based on substance and the quest for a universally best method is quixotic.” Instead, we offer here an important amendment to the ERGM, a model that is already extremely popular across disciplines and is likely to continue to be so. In providing a frailty extension to the ERGM we make it even more widely applicable, since we suspect that there are many contexts where complex interdependencies come with unobserved heterogeneity. Moreover, our model has the positive side effect of overcoming estimation problems in the ERGM that lead to degeneracy.
1.2 The frailty ERGM
An important assumption for identifying Equation (1) is that
![]() $\unicode[STIX]{x1D6E4}(\mathbf{y},\mathbf{x})$
is a vector of sufficient statistics for the network; i.e., the model includes all network- and nodal-level covariates necessary to explain the network. This is a strong assumption. As is the case with standard regression models, excluding covariates that are correlated with both the dependent and independent variables is a threat to inference. In a network model, excluding relevant covariates is likely to be even more damaging to inference given the inherent correlations between network statistics. For instance, in a friendship network, we may believe that the formation of friendships (ties) between individuals is driven by many factors that are measurable; e.g., social class, race, age, etc. However, we may suspect that there are other, intangible factors specific to each individual that are difficult if not impossible to measure, such as “friendliness” or “charisma,” that are also related to network structure (people that are friendlier are likely to have more friends, increasing the centrality of friendly individuals above what we would expect given their other, known attributes). In other words, the observed and measured characteristics are not sufficient for explaining the network we observe. Further, because these unobserved characteristics may be correlated with both the outcome (network structure) and the other explanatory variables, there is the potential for mistaken inferences when such heterogeneity is not accounted for.
$\unicode[STIX]{x1D6E4}(\mathbf{y},\mathbf{x})$
is a vector of sufficient statistics for the network; i.e., the model includes all network- and nodal-level covariates necessary to explain the network. This is a strong assumption. As is the case with standard regression models, excluding covariates that are correlated with both the dependent and independent variables is a threat to inference. In a network model, excluding relevant covariates is likely to be even more damaging to inference given the inherent correlations between network statistics. For instance, in a friendship network, we may believe that the formation of friendships (ties) between individuals is driven by many factors that are measurable; e.g., social class, race, age, etc. However, we may suspect that there are other, intangible factors specific to each individual that are difficult if not impossible to measure, such as “friendliness” or “charisma,” that are also related to network structure (people that are friendlier are likely to have more friends, increasing the centrality of friendly individuals above what we would expect given their other, known attributes). In other words, the observed and measured characteristics are not sufficient for explaining the network we observe. Further, because these unobserved characteristics may be correlated with both the outcome (network structure) and the other explanatory variables, there is the potential for mistaken inferences when such heterogeneity is not accounted for.
The approach we propose to accommodate such unobserved heterogeneity is directly analogous to the use of frailty terms in other applied methods, such as in event history models. In that context, frailty terms—modeled as individual-level random effects—are added to the model to account for unobserved heterogeneity in the units, where it is meant to capture variation in individuals’ susceptibility to disease or death (Vaupel, Manton, and Stallard Reference Vaupel, Manton and Stallard1979). In our case, we introduce individual (or group) random effects into Equation (1) to model unobserved heterogeneity in the propensity for individuals in the network to form ties. To be more concrete, suppose each individual has some level of sociality—i.e., friendliness or charisma in the friendships network example above—which we will call
![]() $s_{i}$
, then Equation (1) could be augmented as such:
$s_{i}$
, then Equation (1) could be augmented as such:
Here
![]() $\sum s_{i}$
is the sum of all of the individual frailty components.Footnote
5
Recall that the ERGM estimates a single probability for the graph as a whole. Thus, the frailties are added as a set to the numerator and denominator (i.e.,
$\sum s_{i}$
is the sum of all of the individual frailty components.Footnote
5
Recall that the ERGM estimates a single probability for the graph as a whole. Thus, the frailties are added as a set to the numerator and denominator (i.e.,
![]() $\unicode[STIX]{x1D705}$
). For identification, they are allowed to vary according to a distribution centered at 0. For the purposes of this paper, we use a normal distribution with mean 0 and a variance,
$\unicode[STIX]{x1D705}$
). For identification, they are allowed to vary according to a distribution centered at 0. For the purposes of this paper, we use a normal distribution with mean 0 and a variance,
![]() $\unicode[STIX]{x1D70E}_{s}^{2}$
, to be estimated from the data; i.e.,
$\unicode[STIX]{x1D70E}_{s}^{2}$
, to be estimated from the data; i.e.,
![]() $s_{i}\sim N(0,\unicode[STIX]{x1D70E}_{s}^{2})$
. To model a greater degree of variability, distributions with more mass in the tails could certainly be used. Notice that, because
$s_{i}\sim N(0,\unicode[STIX]{x1D70E}_{s}^{2})$
. To model a greater degree of variability, distributions with more mass in the tails could certainly be used. Notice that, because
![]() $E[s_{i}]=0$
, modeling the frailty term as being centered at zero has a key advantage of leaving the probability of the graph fixed in expectation, though the variance increases.
$E[s_{i}]=0$
, modeling the frailty term as being centered at zero has a key advantage of leaving the probability of the graph fixed in expectation, though the variance increases.
Our proposed extension is directly applicable to directed networks, though in this case we would include sender and receiver effects—one each for each individual (or group)—in the network. In this case, the objective is to model heterogeneity in the probability that actors in the network send ties (the sender effect) and the probability they accept ties (the receiver effect). We model these effects as having a joint Gaussian distribution centered at zero,
where
![]() $\unicode[STIX]{x1D70E}_{s}^{2}$
and
$\unicode[STIX]{x1D70E}_{s}^{2}$
and
![]() $\unicode[STIX]{x1D70E}_{r}^{2}$
are the variances of the sender and receiver effects, respectively, and
$\unicode[STIX]{x1D70E}_{r}^{2}$
are the variances of the sender and receiver effects, respectively, and
![]() $\unicode[STIX]{x1D70E}_{sr}$
is their covariance, each to be estimated from the data. In terms of the ERGM, including these sender and receiver effects would result in the following model to be estimated:
$\unicode[STIX]{x1D70E}_{sr}$
is their covariance, each to be estimated from the data. In terms of the ERGM, including these sender and receiver effects would result in the following model to be estimated:
As in Equation (2) and the sociality effects, the sender and receiver effects are included as additive terms in the numerator and denominator. For the remainder of this paper, we focus on the undirected frailty model of Equation (2), though it should be clear that the directed case is a relatively straightforward extension.
1.3 Estimation
Estimation of the proposed FERGM was performed using a novel application of a (logistic) multiple-membership mixed-effects model, which is a model developed by education researchers for the purpose of modeling student performance in cases where students may have moved between classrooms (or other groups) during a period being studied (Goldstein Reference Goldstein2003, ch. 13). In that context, researchers are often interested in the performance of students on standardized tests and wish to account for the hierarchical structure of the data generating process, where students are nested in classrooms, which are themselves nested in schools, etc. If students never move classrooms (schools), then a standard hierarchical model is easily applied. However, the situation is complicated when students are assigned to multiple classrooms. In that case, researchers need to adjust for the fact that students can spend a portion of their time in multiple classrooms. Multiple-membership models are one tool that has been developed for just such a situation.
In the case of the proposed network model, instead of modeling the performance of students, we model the occurrence of ties between two nodes. In our application of the model, each (potential) tie,
![]() $y_{ij}$
, is estimated as being associated with two groups—one being the group associated with node
$y_{ij}$
, is estimated as being associated with two groups—one being the group associated with node
![]() $i$
and the other with node
$i$
and the other with node
![]() $j$
. More concretely, in the undirected case each tie in this model is estimated as follows
$j$
. More concretely, in the undirected case each tie in this model is estimated as follows
Here,
![]() $s_{i}$
and
$s_{i}$
and
![]() $s_{j}$
are the random effects associated with nodes
$s_{j}$
are the random effects associated with nodes
![]() $i$
and
$i$
and
![]() $j$
,
$j$
,
![]() $\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6E4}(\mathbf{y},\mathbf{x})$
is a vector of change statistics (those corresponding with the sufficient statistics of Equation (1)) for when the tie between
$\unicode[STIX]{x1D6E5}\unicode[STIX]{x1D6E4}(\mathbf{y},\mathbf{x})$
is a vector of change statistics (those corresponding with the sufficient statistics of Equation (1)) for when the tie between
![]() $i$
and
$i$
and
![]() $j$
is toggled, while
$j$
is toggled, while
![]() $\unicode[STIX]{x1D703}$
is the coefficient on these change statistics. In other words, if you were to exclude the random effects, you would recover the maximum pseudolikelihood model for the standard ERGM.
$\unicode[STIX]{x1D703}$
is the coefficient on these change statistics. In other words, if you were to exclude the random effects, you would recover the maximum pseudolikelihood model for the standard ERGM.
Estimating the FERGM in this way has both advantages and disadvantages. On the one hand, the FERGM can be estimated with many standard mixed-effects modeling packages (we will use R and Stan in the Monte Carlo and examples below), estimated much more quickly for larger networks, and is less susceptible to issues of degeneracy when compared to the MCMC-MLE approach. On the other hand, estimating the model in a way that extends the maximum pseudolikelihood approach potentially opens up issues of efficiency and excessively optimistic inferences, which are a weakness of that approach. However, our Monte Carlos as well as the below applications suggest that the robustness of our estimation strategy to issues of degeneracy should outweigh those concerns for most analysts.
2 Monte Carlo Analysis
In this section, we present the results of an extensive Monte Carlo analysis. The objective of this analysis is to compare, under controlled conditions, the performance of the proposed FERGM to the standard ERGM when unobserved heterogeneity is present in the network formation process. To foreshadow our results, we find that the performance of the FERGM, as measured by the root-mean-squared error of the errors, significantly outperforms the standard ERGM in a number of contexts.
2.1 Network simulation
The first step of the Monte Carlo analysis was to simulate a set of networks of various sizes and specifications.Footnote
6
Undirected networks of
![]() $n\in \{25,\,50,\,100\}$
nodes were specified. To approximate the type of networks that may be encountered in applied research, while still keeping the data generating process relatively simple, the model used to generate these networks included: the overall network density, measured by the number of edges (ties) in the network; a transitivity effect, measured by the geometrically weighted edgewise shared partner distribution (gwesp; Snijders et al.
Reference Snijders, Pattison, Robins and Handcock2006);Footnote
7
and two node-level homophily effects. For the first nodal covariate,
$n\in \{25,\,50,\,100\}$
nodes were specified. To approximate the type of networks that may be encountered in applied research, while still keeping the data generating process relatively simple, the model used to generate these networks included: the overall network density, measured by the number of edges (ties) in the network; a transitivity effect, measured by the geometrically weighted edgewise shared partner distribution (gwesp; Snijders et al.
Reference Snijders, Pattison, Robins and Handcock2006);Footnote
7
and two node-level homophily effects. For the first nodal covariate,
![]() $\text{group}_{i}$
, each node was randomly assigned with equal probability to one of two groups. For the second nodal covariate, a continuous value for each node was drawn from a standard normal distribution,
$\text{group}_{i}$
, each node was randomly assigned with equal probability to one of two groups. For the second nodal covariate, a continuous value for each node was drawn from a standard normal distribution,
![]() $\unicode[STIX]{x1D70E}_{i}\sim N(0,\,1)$
.
$\unicode[STIX]{x1D70E}_{i}\sim N(0,\,1)$
.
In notation, the data generating process used for the simulated networks was as follows:Footnote 8
 $$\begin{eqnarray}\displaystyle \Pr (Y=y\mid \cdot ) & = & \displaystyle \frac{1}{\unicode[STIX]{x1D705}}\exp \left\{-3.25\times \text{edges}_{y}+0.75\times \text{gwesp}_{y}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,0.25\times \mathop{\sum }_{i,j\in y}\mathbf{1}(\text{group}_{i}=\text{group}_{j})+\unicode[STIX]{x1D6FE}\times \mathop{\sum }_{i,j\in y}|\unicode[STIX]{x1D70E}_{i}-\unicode[STIX]{x1D70E}_{j}|\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \Pr (Y=y\mid \cdot ) & = & \displaystyle \frac{1}{\unicode[STIX]{x1D705}}\exp \left\{-3.25\times \text{edges}_{y}+0.75\times \text{gwesp}_{y}\right.\nonumber\\ \displaystyle & & \displaystyle \left.+\,0.25\times \mathop{\sum }_{i,j\in y}\mathbf{1}(\text{group}_{i}=\text{group}_{j})+\unicode[STIX]{x1D6FE}\times \mathop{\sum }_{i,j\in y}|\unicode[STIX]{x1D70E}_{i}-\unicode[STIX]{x1D70E}_{j}|\right\}.\end{eqnarray}$$
Here
![]() $\mathbf{1}(\cdot )$
is the indicator function and is equal to 1 if
$\mathbf{1}(\cdot )$
is the indicator function and is equal to 1 if
![]() $i$
and
$i$
and
![]() $j$
belong to the same group and 0 otherwise. In other words, this defines a dummy variable that indicates shared group membership and will have the effect of increasing the likelihood of a tie between nodes in the same group.
$j$
belong to the same group and 0 otherwise. In other words, this defines a dummy variable that indicates shared group membership and will have the effect of increasing the likelihood of a tie between nodes in the same group.
As indicated in (6), the vector of coefficients was set to
![]() $\unicode[STIX]{x1D703}=(-3.25,0.75,0.25,\unicode[STIX]{x1D6FE})$
. The coefficient on the continuous node-level homophily effect,
$\unicode[STIX]{x1D703}=(-3.25,0.75,0.25,\unicode[STIX]{x1D6FE})$
. The coefficient on the continuous node-level homophily effect,
![]() $\unicode[STIX]{x1D6FE}$
, varied in increments of
$\unicode[STIX]{x1D6FE}$
, varied in increments of
![]() $0.25$
from
$0.25$
from
![]() $0.0$
to
$0.0$
to
![]() $-1.0$
; i.e.,
$-1.0$
; i.e.,
![]() $\unicode[STIX]{x1D6FE}\in \{0,-0.25,-0.50,-0.75,-1.0\}$
. By varying the coefficient on the unobserved heterogeneity in this way, we are able to test the performance of the ERGM and FERGM on networks for which the importance of the unobserved heterogeneity in the data generating process varies.Footnote
9
$\unicode[STIX]{x1D6FE}\in \{0,-0.25,-0.50,-0.75,-1.0\}$
. By varying the coefficient on the unobserved heterogeneity in this way, we are able to test the performance of the ERGM and FERGM on networks for which the importance of the unobserved heterogeneity in the data generating process varies.Footnote
9
Overall, the above model produced 15 different data generating processes (three network sizes, five levels of heterogeneity). For each of these, random networks were generated following a three-step procedure. First, an undirected basis network was generated with a default density of 0.15.Footnote 10 Second, nodal covariates were assigned as specified above in Equation (6). Third, using the modified basis network, 1008 networks were simulated for the given network coefficient specification.Footnote 11 A summary of model specifications and average network densities is presented in Table 1 and six selected networks are show in Figure 1. As reported, network densities remain relatively stable—they do not display any tendency toward 0 or 1—thus we were confident the chosen specification does not produce degenerate networks across the range of network sizes used.Footnote 12
Table 1. Summary of network densities for the networks generated in the Monte Carlo study.

Note: 1008 undirected, binary networks were drawn for each specification. The values for
![]() $\unicode[STIX]{x1D6FE}$
refer to the coefficient on the individual-level unobserved heterogeneity term, which was drawn from a Gaussian distribution with
$\unicode[STIX]{x1D6FE}$
refer to the coefficient on the individual-level unobserved heterogeneity term, which was drawn from a Gaussian distribution with
![]() $\unicode[STIX]{x1D707}=0$
and
$\unicode[STIX]{x1D707}=0$
and
![]() $\unicode[STIX]{x1D70E}=1$
. Full model specifications are found in Equation (6).
$\unicode[STIX]{x1D70E}=1$
. Full model specifications are found in Equation (6).
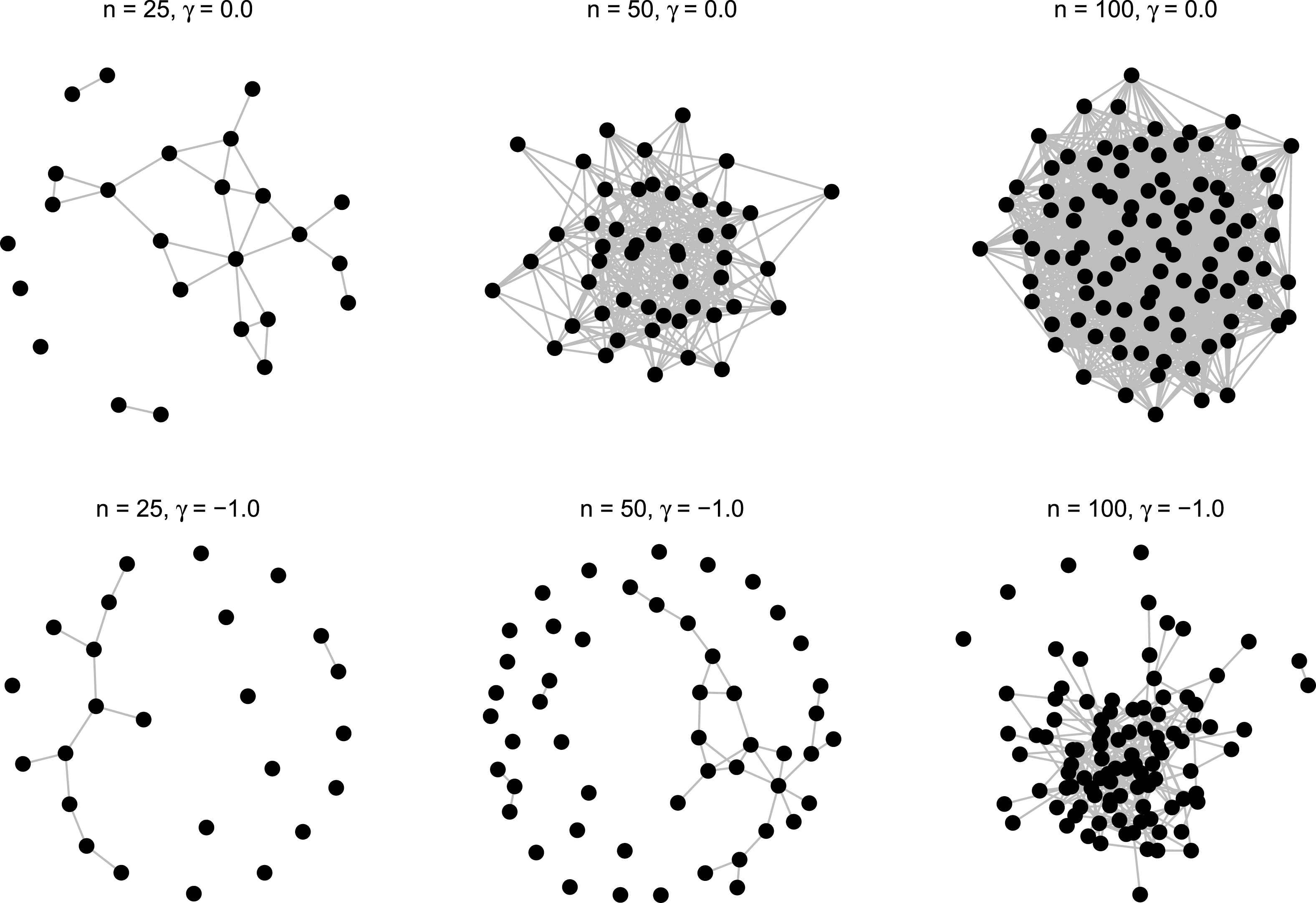
Figure 1. Example networks.
2.2 Model estimation and evaluation
The second task in our preliminary Monte Carlo assessment of the proposed FERGM is to estimate the models using the networks simulated as described in the previous section. Since we are interested in the comparative performance of the ERGM and FERGM in the presence of unobserved heterogeneity, we purposefully excluded from the estimation of the models the node-level continuous homophily term included in the network simulations; i.e., the last term involving
![]() $\unicode[STIX]{x1D6FE}$
in Equation (6).
$\unicode[STIX]{x1D6FE}$
in Equation (6).
The standard ERGM was estimated through the state-of-the-art Markov Chain Monte Carlo MLE (MCMC-MLE) methodology. In the MCMC-MLE approach, the denominator of Equation (1) is approximated with a large sample from the universe of possible networks given the previous iteration’s estimates of
![]() $\unicode[STIX]{x1D703}$
. After many iterations, estimates of
$\unicode[STIX]{x1D703}$
. After many iterations, estimates of
![]() $\unicode[STIX]{x1D703}$
are guaranteed to converge. However, while the MCMC-MLE methodology has better theoretical properties than the alternative maximum pseudolikelihood (MPLE) approach, (see, e.g., Robins et al.
Reference Robins, Pattison, Kalish and Lusher2007), it can suffer from issues of degeneracy (Snijders Reference Snijders2002; Snijders et al.
Reference Snijders, Pattison, Robins and Handcock2006).Footnote
13
For this reason, we took a multistep approach to avoid issues of degeneracy and to ensure convergence. In the first step, initial values for
$\unicode[STIX]{x1D703}$
are guaranteed to converge. However, while the MCMC-MLE methodology has better theoretical properties than the alternative maximum pseudolikelihood (MPLE) approach, (see, e.g., Robins et al.
Reference Robins, Pattison, Kalish and Lusher2007), it can suffer from issues of degeneracy (Snijders Reference Snijders2002; Snijders et al.
Reference Snijders, Pattison, Robins and Handcock2006).Footnote
13
For this reason, we took a multistep approach to avoid issues of degeneracy and to ensure convergence. In the first step, initial values for
![]() $\unicode[STIX]{x1D703}$
were generated by taking (up to) four iterations of the algorithm.Footnote
14
In the second step, the algorithm was restarted using the estimates from the first step as the initial values. In this step, the algorithm was run for up to 20 iterations, or until convergence (as determined by a lack of a change in the log-likelihood). For situations where the model failed to converge during the second stage, another 10 more attempts were made (with 20 iterations of the algorithm included during each attempt), with the initial values set to those from the previous attempt. If, after all of this, the model still failed to converge, the network was discarded for nonconvergence.Footnote
15
$\unicode[STIX]{x1D703}$
were generated by taking (up to) four iterations of the algorithm.Footnote
14
In the second step, the algorithm was restarted using the estimates from the first step as the initial values. In this step, the algorithm was run for up to 20 iterations, or until convergence (as determined by a lack of a change in the log-likelihood). For situations where the model failed to converge during the second stage, another 10 more attempts were made (with 20 iterations of the algorithm included during each attempt), with the initial values set to those from the previous attempt. If, after all of this, the model still failed to converge, the network was discarded for nonconvergence.Footnote
15

Figure 2. Monte Carlo results.
Estimation of the FERGM was more straightforward. The FERGM was estimated as a multiple-membership mixed-effects model, as described in Section 1.3, in Stan (Stan Development Team 2015). As the Monte Carlos focus on undirected networks, each node’s random component was modeled as drawn from a single normal distribution, centered at zero with variance
![]() $\unicode[STIX]{x1D70E}_{w}$
, with the assumption that
$\unicode[STIX]{x1D70E}_{w}$
, with the assumption that
![]() $\unicode[STIX]{x1D70E}_{w}$
was drawn from a Cauchy distribution centered at zero with a dispersion of 2. The parameters for the endogenous structural parameter and the exogenous covariates were given diffuse normal priors centered at zero with a standard deviation of 10.Footnote
16
$\unicode[STIX]{x1D70E}_{w}$
was drawn from a Cauchy distribution centered at zero with a dispersion of 2. The parameters for the endogenous structural parameter and the exogenous covariates were given diffuse normal priors centered at zero with a standard deviation of 10.Footnote
16
2.3 Results
Overall results for the Monte Carlo study are presented in Figure 2. Each of the panels shows the (scaled) root-mean-squared error for coefficient estimatesFootnote 17 on the vertical axis and the level of the unobserved heterogeneity on the horizontal axis. The first column of panels shows networks with 25 nodes, the center column 50-node networks, and the right column 100-node networks. Each rows reports the results for a different covariate. Results for the ERGM are reported as dotted lines and open circles, while the FERGM results are shown as solid lines and closed circles.
The general takeaway from these results is that, on average, the FERGM performs better than the standard ERGM in the presence of unobserved heterogeneity. In six of nine panels, the FERGM reports lower RMSE than the standard ERGM at any level of unobserved heterogeneity. In the other three cases, the differences in performance are slight. It is important to note that the scales of the y-axes in these three are quite small. Furthermore, two of the cases in which the ERGM seems to outperform the FERGM are for the coefficient on the exogenous homophily covariate for the 50- and 100-node networks (bottom row, right two columns). Since the unobserved heterogeneity was, by construction, not correlated with this covariate, it should not be surprising that the ERGM performed well.
On the other hand, when the ERGM is wrong, it is often significantly so. For instance, take the GWESP structural term for the 100-node networks. Scholars are often interested in this term, as such a parameterization of transitivity tends to explain much about how a network is structured (see, e.g., Goodreau, Kitts, and Morris Reference Goodreau, Kitts and Morris2009). In this case, the presence of unobserved heterogeneity leads to RMSEs that are more than 3 times the size of those produced by the FERGM. That is, when the FERGM does better, it generally does so by a huge margin relative to the scale of the coefficient. Overall then, the results are strongly in favor of the FERGM. The ERGM and FERGM perform similarly in only a few cases: for the mid- and large-sized networks the ERGM performs relatively well on the exogenous covariate; ERGM also does well on the endogenous terms for the mid-sized network. However, it fails otherwise, and when it fails, it does so by large margins, which makes inferences based on the ERGM more problematic.
Finally, it should be noted that these results should be considered as a best-case scenario for the standard ERGM. A great deal of effort went into estimating each of these networks and assuring that the model had converged (see Section 2.2). When there was some question as to the convergence status, the network was dropped. This means the Monte Carlo study was designed conservatively, in favor of the standard ERGM. Because convergence in the ERGM may be hampered by heterogeneity, evidence of some of the worst performing ERGMs are not included in the results. Even with these precautions in place, these results suggest the standard ERGM is very fragile in the face of unobserved heterogeneity and that our proposed FERGM can play an important role when such heterogeneity exists.Footnote 18
3 Applications
While the previous section demonstrated the potential importance of directly modeling unobserved heterogeneity in nodal covariates in simulated network data, there remains a question as to how the model we propose will function in practical, real-world problems. For this reason, in this section we turn to two networks that have played an important role in the networks literature: the Lazega (Reference Lazega2001) law firm collaboration network and the Magnolia High network (Resnick et al. Reference Resnick, Bearman, Blum, Bauman, Harris, Jones, Tabor, Beuhring, Sieving and Shew1997).
3.1 Lazega law firm collaboration network
The first example we turn to is the Lazega (Reference Lazega2001) law firm collaboration network. This undirected network consists of 36 attorneys (nodes) in three New England offices: 22 attorneys were located in Boston, 13 in Hartford, and 1 in Providence. There were three female attorneys in the data set, all of which were located in the Boston office. In addition to each attorney’s office and gender, the network includes data on attorneys’ seniority, and whether they were in litigation or corporate practice. Overall, there are 115 ties (density of 18.3%). The network is shown in Figure 3, with the female attorneys in red.

Figure 3. Lazega (Reference Lazega2001) Law Firm Collaboration Network. This is an undirected network recording collaborations between the 36 attorneys. The three female attorneys are highlighted in black.
The Lazega network has been used in a number of studies investigating the properties of ERGMs. In addition to acting as a template for the simulated networks explored in the Monte Carlo analysis, van Duijn, Gile, and Handcock (Reference van Duijn, Gile and Handcock2009) used the network in an important study comparing the performance of the MPLE and MCMC-MLE approaches to estimating ERGMs, while Hunter and Handcock (Reference Hunter and Handcock2006) used the network as an example in their development of curved exponential family models.Footnote 19 In other words, the Lazega network is considered to be well understood and it quite amenable to analysis with ERGMs. This makes it an excellent example to gauge the performance of the proposed FERGM.
For this analysis, we have adopted an identical model specification to the one used in van Duijn, Gile, and Handcock (Reference van Duijn, Gile and Handcock2009). The ERGM and FERGM included an edge term, homophily terms for practice, gender, and office; nodal covariates for seniority and practice; and, to account for the network structure, the model included a geometrically weighted edgewise shared partner term (with decay equal to 0.7781, as in van Duijn, Gile, and Handcock (Reference van Duijn, Gile and Handcock2009)). The ERGM was estimated with MCMC-MLE, as is current standard practice in the network sciences, while the FERGM was estimated as a Bayesian multiple-membership model, as in the Monte Carlos in the previous section.Footnote 20

Figure 4. ERGM and FERGM results for the Lazega law firm collaboration network.
The coefficients estimates along with 95% confidence (credible) intervals for these estimated models are reported in Figure 4.Footnote 21 Estimated from the standard ERGM are reported in black, while the FERGM results are in red. As expected, the coefficient estimates for the ERGM agree with those published by van Duijn, Gile, and Handcock (Reference van Duijn, Gile and Handcock2009), while each of these coefficients is also statistically significant at the 95% confidence level (as shown by the confidence intervals excluding zero). The posterior means for the FERGM also largely agree with the standard ERGM results.
The difference between these models emerges when we turn to comparing the confidence intervals of the ERGM with the credible intervals of the FERGM. On average, the FERGM credible intervals are wider than the ERGM confidence intervals. In most cases this does not make a large difference to the inferences we can draw from the model; however, in one important case it does. Notice that the credible interval for the gender homophily term increases significantly in the FERGM when compared to the standard ERGM. In the case of the FERGM, the credible interval includes zero, suggesting that the effect of gender homophily is not statistically different from zero.
Looking more carefully at the network we see that the results for the FERGM are more reasonable than those of the standard ERGM. Recall that there are only three (of 36) women in the network. Of the potential 630 ties in the network, only three of them represent potential gender homophily effects between women and only one of these is a tie. In other words, there is very little data from which we can make the claim that gender homophily is important to the formation of this network; i.e., the results from the standard ERGM seem unreasonably certain about this effect. On the other hand, the proposed FERGM, by incorporating the potential for other unobserved nodal factors, is more conservative.
As an additional check on the relative performance of the two models, we also performed a straightforward predictive analysis through simulation. For the estimated ERGM, we simulated 500 networks, extracted the adjacency matrix, and then calculated the percentage of ties that were correctly predicted in each of these. For the FERGM, we calculated the predicted probability of a tie for each of the 500 posterior draws of the estimated parameters, used these predicted probabilities to take a single draw from a Bernoulli distribution for each dyad in the network, then calculated the percent correctly predicted. Calculating the mean percentage correctly predicted for each of these sets of simulations, we found that, on average, the FERGM outperformed the standard ERGM by approximately 5% (79.7% for the FERGM versus 74.6% for the ERGM).

Figure 5. Magnolia high friendship network.
3.2 Magnolia high friendship network
The second network we investigate is the Magnolia High friendship network, which was first reported in Resnick et al. (Reference Resnick, Bearman, Blum, Bauman, Harris, Jones, Tabor, Beuhring, Sieving and Shew1997). This network is generated from a model of adolescent friendship networks in a large high school in the Southern U.S. Because it is constructed from a well-fitting model of the observed network, the data generating process is known. Thus, the network allows us to explore the behavior of the FERGM in another large, real-world example, but one in which we should expect little to no unobserved heterogeneity. This example, then, gives us an idea of the effect of using the FERGM in a case where a standard ERGM would be sufficient. Should the FERGM differ significantly from the ERGM then analysts should be cautious in applying the FERGM. Alternatively, should the FERGM do no harm, then analysts risk little in applying the FERGM whenever there is reason to suspect unobserved heterogeneity.
Overall, the Magnolia High network has 1461 students across five grades (7th to the 12th). The network includes 974 undirected ties for a density of 0.09%. The network includes data on each node’s grade, race, and sex. The full network is presented in Figure 5, with nodes colored by their grade.
For estimating the ERGM and FERGM for the Magnolia High network, we have adopted the same model specified to generate the model. This included a term for the number of edges, a geometrically weighted edgewise shared partner term (decay fixed at 0.25), and homophily terms on grade, race, and sex.Footnote 22

Figure 6. ERGM and FERGM results for the magnolia high friendship network.
The results for the ERGM and FERGM estimates are shown in Figure 6. As before, point estimates and confidence intervals for the ERGM are shown in black, while the FERGM posterior means and credible intervals are shown in red. Unlike in the case of the Lazega network, there is not much of interest to report; i.e., the ERGM and FERGM results are in agreement on all of the covariates. In other words, in this large network with a known data generating process and little suspicion of unobserved heterogeneity, the FERGM does no harm.Footnote 23
4 Discussion
Network data, virtually regardless of the application area, are likely to exhibit unobserved heterogeneity. It is, at the very least, difficult to rule out a priori. Our simulations show that given heterogeneity, ERGMs often fall short. Under these circumstances, a modeling strategy that is robust to heterogeneity is desirable. Here the FERGM looks promising. FERGMs directly estimate the effects of heterogeneity, which make for more reliable estimates of network structure. Moreover, when the FERGM outperforms the ERGM it generally does so by large margins.
In addition, our novel estimation approach, using a particular form of mixed-effects models, opens up numerous avenues for future research. In simulated and substantive networks, we have shown that using a mixed-effects model to estimate the FERGM leads to similar inferences, even when we expect little to no unobserved heterogeneity. Our model has the important advantage of avoiding the issues of degeneracy that present serious obstacles to the estimation of ERGMs via MCMC-MLE in all but the simplest networks. Further exploration of the application of well-known mixed-effects modeling techniques to exponential family network models could lead to advances in modeling more complex network generating processes without making scholars dependent on fragile estimation methods.
We suspect that advances in the development and application of network modeling, such as this, will be useful throughout the social sciences and a host of other areas that are interested in modeling complex interdependencies. In addition, the methodology may help practitioners in the public policy and national security arenas who rely on the evaluation of coalition strategies and relationships more accurately assess the role of policies and conditions. Further, at least one of the applications appears to advance its own substantive literature, reducing the value of gender in the generation of ties between lawyers.
There are, however, important caveats to this work. The simulations and substantive applications do not comprise an exhaustive set of networks. Thus, while we believe that this paper provides an invaluable extension to modeling network complexity where there is likely to be unobserved heterogeneity, further work is necessary to fully understand the properties of the FERGM and the tradeoffs with the ERGM. This is especially important given the myriad of ERGM terms and several ways in which unobserved heterogeneity may exist in a network. Moreover, the frailty extension is not a substitute for appropriately modeling link formation with the observed data in the context of the ERGM. First and foremost, scholars need to embark on the nontrivial task of specifying their models with the appropriate endogenous and exogenous terms. Provided they have met with success there, employing the FERGM when there is believed to be remaining unobserved heterogeneity would be a logical next step.











