No CrossRef data available.
Article contents
A REALIZATION OF THE ENVELOPING SUPERALGEBRA 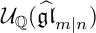 $ {\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
$ {\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
Published online by Cambridge University Press: 09 September 2021
Abstract
In [2], Beilinson–Lusztig–MacPherson (BLM) gave a beautiful realization for quantum
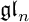 $\mathfrak {gl}_n$
via a geometric setting of quantum Schur algebras. We introduce the notion of affine Schur superalgebras and use them as a bridge to link the structure and representations of the universal enveloping superalgebra
$\mathfrak {gl}_n$
via a geometric setting of quantum Schur algebras. We introduce the notion of affine Schur superalgebras and use them as a bridge to link the structure and representations of the universal enveloping superalgebra
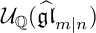 ${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
of the loop algebra
${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
of the loop algebra
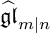 $\widehat {\mathfrak {gl}}_{m|n}$
of
$\widehat {\mathfrak {gl}}_{m|n}$
of
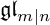 ${\mathfrak {gl}}_{m|n}$
with those of affine symmetric groups
${\mathfrak {gl}}_{m|n}$
with those of affine symmetric groups
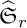 ${\widehat {{\mathfrak S}}_{r}}$
. Then, we give a BLM type realization of
${\widehat {{\mathfrak S}}_{r}}$
. Then, we give a BLM type realization of
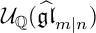 ${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
via affine Schur superalgebras.
${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
via affine Schur superalgebras.
The first application of the realization of
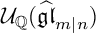 ${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
is to determine the action of
${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
is to determine the action of
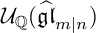 ${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
on tensor spaces of the natural representation of
${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
on tensor spaces of the natural representation of
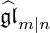 $\widehat {\mathfrak {gl}}_{m|n}$
. These results in epimorphisms from
$\widehat {\mathfrak {gl}}_{m|n}$
. These results in epimorphisms from
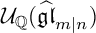 $\;{\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
to affine Schur superalgebras so that the bridging relation between representations of
$\;{\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
to affine Schur superalgebras so that the bridging relation between representations of
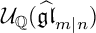 ${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
and
${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
and
 ${\widehat {{\mathfrak S}}_{r}}$
is established. As a second application, we construct a Kostant type
${\widehat {{\mathfrak S}}_{r}}$
is established. As a second application, we construct a Kostant type
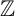 $\mathbb Z$
-form for
$\mathbb Z$
-form for
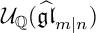 ${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
whose images under the epimorphisms above are exactly the integral affine Schur superalgebras. In this way, we obtain essentially the super affine Schur–Weyl duality in arbitrary characteristics.
${\mathcal U}_{\mathbb Q}(\widehat {\mathfrak {gl}}_{m|n})$
whose images under the epimorphisms above are exactly the integral affine Schur superalgebras. In this way, we obtain essentially the super affine Schur–Weyl duality in arbitrary characteristics.
MSC classification
- Type
- Article
- Information
- Copyright
- © (2021) The Authors. The publishing rights in this article are licenced to Foundation Nagoya Mathematical Journal under an exclusive license
Footnotes
Supported by the National Natural Science Foundation of China (11671297, 11871404)





