Article contents
ON SEPARABLE 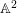 $\mathbb{A}^{2}$ AND
$\mathbb{A}^{2}$ AND 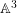 $\mathbb{A}^{3}$-FORMS
$\mathbb{A}^{3}$-FORMS
Published online by Cambridge University Press: 26 December 2018
Abstract
In this paper, we will prove that any 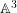 $\mathbb{A}^{3}$-form over a field
$\mathbb{A}^{3}$-form over a field 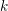 $k$ of characteristic zero is trivial provided it has a locally nilpotent derivation satisfying certain properties. We will also show that the result of Kambayashi on the triviality of separable
$k$ of characteristic zero is trivial provided it has a locally nilpotent derivation satisfying certain properties. We will also show that the result of Kambayashi on the triviality of separable 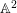 $\mathbb{A}^{2}$-forms over a field
$\mathbb{A}^{2}$-forms over a field 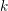 $k$ extends to
$k$ extends to 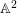 $\mathbb{A}^{2}$-forms over any one-dimensional Noetherian domain containing
$\mathbb{A}^{2}$-forms over any one-dimensional Noetherian domain containing 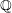 $\mathbb{Q}$.
$\mathbb{Q}$.
MSC classification
- Type
- Article
- Information
- Copyright
- © 2018 Foundation Nagoya Mathematical Journal
References
- 1
- Cited by



