Article contents
CONTINUITY OF HILBERT–KUNZ MULTIPLICITY AND F-SIGNATURE
Published online by Cambridge University Press: 27 December 2018
Abstract
We establish the continuity of Hilbert–Kunz multiplicity and F-signature as functions from a Cohen–Macaulay local ring 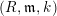 $(R,\mathfrak{m},k)$ of prime characteristic to the real numbers at reduced parameter elements with respect to the
$(R,\mathfrak{m},k)$ of prime characteristic to the real numbers at reduced parameter elements with respect to the 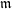 $\mathfrak{m}$-adic topology.
$\mathfrak{m}$-adic topology.
- Type
- Article
- Information
- Copyright
- © 2018 Foundation Nagoya Mathematical Journal
Footnotes
Polstra was supported in part by NSF Postdoctoral Research Fellowship DMS #1703856.
References
A correction has been issued for this article:
- 4
- Cited by
Linked content
Please note a has been issued for this article.



