Hostname: page-component-848d4c4894-8kt4b Total loading time: 0 Render date: 2024-06-21T17:50:02.775Z Has data issue: false hasContentIssue false
  • English
  • Français

Developing a novel continuum model of static and dynamic contact angles in a case study of a water droplet on micro-patterned hybrid substrates

Published online by Cambridge University Press:  06 November 2018

Arash Azimi ,
Ping He Open the ORCID record for Ping He [Opens in a new window] ,
Chae Rohrs  and
Chun-Wei Yao
Arash Azimi
Affiliation:
Department of Mechanical Engineering, Lamar University, Beaumont, TX 77710, USA
Ping He*
Affiliation:
Department of Mechanical Engineering, Lamar University, Beaumont, TX 77710, USA
Chae Rohrs
Affiliation:
Department of Mechanical Engineering, Lamar University, Beaumont, TX 77710, USA
Chun-Wei Yao
Affiliation:
Department of Mechanical Engineering, Lamar University, Beaumont, TX 77710, USA
*
Address all correspondence to Ping He at phe@lamar.edu
Get access

Abstract

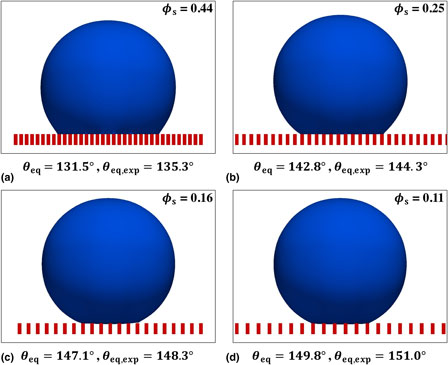
Modeling static and dynamic contact angles is a great challenge in studying wetting and de-wetting. We propose a new slip boundary model based on the Navier–Stokes equations, and establish a realistic continuum approach to simulate the contact line dynamics in 3-D. To validate our model, a water droplet interacting with micrometer-sized patterns of a hybrid hydro-phobic/-philic surface is studied numerically and compared with experimental measurements. Good agreement has been observed with four pillar spacings in the static, receding, and advancing modes. Moreover, details of the droplet–surface interaction are revealed, i.e., penetrations, sagging, local, and global contact angles.

Type
Research Letters
Information
MRS Communications , Volume 8 , Issue 4 , December 2018 , pp. 1445 - 1454
Copyright
Copyright © Materials Research Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Young, T.: An essay on the cohesion of fluids. Philos. Trans. R. Soc. Lond. 95, 65 (1805).Google Scholar
2.Wenzel, R.N.: Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 28, 988 (1936).10.1021/ie50320a024Google Scholar
3.Cassie, A.B.D. and Baxter, S.: Wettability of porous surfaces. Trans. Faraday Soc. 40, 0546 (1944).10.1039/tf9444000546Google Scholar
4.Huh, C. and Scriven, L.E.: Hydrodynamic model of steady movement of a solid/liquid/fluid contact line. J. Colloid. Interface Sci. 35, 85 (1971).10.1016/0021-9797(71)90188-3Google Scholar
5.Thompson, P.A. and Robbins, M.O.: Simulations of contact-line motion: slip and the dynamic contact angle. Phys. Rev. Lett. 63, 766 (1989).10.1103/PhysRevLett.63.766Google Scholar
6.Blake, T.D. and Haynes, J.M.: Kinetics of liquid/liquid displacement. J. Colloid. Interface Sci. 30, 421 (1969).10.1016/0021-9797(69)90411-1Google Scholar
7.Blake, T.D., Clarke, A., DeConinck, J., and de Ruijter, M.J.: Contact angle relaxation during droplet spreading: comparison between molecular kinetic theory and molecular dynamics. Langmuir 13, 2164 (1997).10.1021/la962004gGoogle Scholar
8.Lim, C.Y. and Lam, Y.C.: Phase-field simulation of impingement and spreading of micro-sized droplet on heterogeneous surface. Microfluid. Nanofluid. 17, 131 (2014).10.1007/s10404-013-1284-8Google Scholar
9.Maxwell, J.C.: VII. On stresses in rarified gases arising from inequalities of temperature. Philos. Trans. R. Soc. Lond. 170, 231 (1879).Google Scholar
10.Qian, T.Z., Wu, C.M., Lei, S.L., Wang, X.P., and Sheng, P.: Modeling and simulations for molecular scale hydrodynamics of the moving contact line in immiscible two-phase flows. J. Phys.: Condens. Matter 21, 464119 (2009).Google Scholar
11.Qian, T.Z., Wang, X.P., and Sheng, P.: Molecular scale contact line hydrodynamics of immiscible flows. Phys. Rev. E 68, 016306 (2003).10.1103/PhysRevE.68.016306Google Scholar
12.Yamamoto, Y., Higashida, S., Tanaka, H., Wakimoto, T., Ito, T., and Katoh, K.: Numerical analysis of contact line dynamics passing over a single wettable defect on a wall. Phys. Fluids 28, 082109 (2016).10.1063/1.4961490Google Scholar
13.Ren, W.Q. and E, W.N.: Boundary conditions for the moving contact line problem. Phys. Fluids 19, 022101 (2007).10.1063/1.2646754Google Scholar
14.Ren, W.Q., Hu, D., and E, W.N.: Continuum models for the contact line problem. Phys. Fluids 22, 102103 (2010).10.1063/1.3501317Google Scholar
15.Ren, W.Q. and E, W.N.: Derivation of continuum models for the moving contact line problem based on thermodynamic principles. Commun. Math. Sci. 9, 597 (2011).10.4310/CMS.2011.v9.n2.a13Google Scholar
16.Ren, W.Q. and Weinan, E.: Contact line dynamics on heterogeneous surfaces. Phys. Fluids 23, 072103 (2011).10.1063/1.3609817Google Scholar
17.Xu, J.J. and Ren, W.Q.: A level-set method for two-phase flows with moving contact line and insoluble surfactant. J. Comput. Phys. 263, 71 (2014).10.1016/j.jcp.2014.01.012Google Scholar
18.Zhang, Z., Xu, S.X., and Ren, W.Q.: Derivation of a continuum model and the energy law for moving contact lines with insoluble surfactants. Phys. Fluids 26, 062103 (2014).10.1063/1.4881195Google Scholar
19.Ren, W.Q., Trinh, P.H., and Weinan, E.: On the distinguished limits of the Navier slip model of the moving contact line problem. J. Fluid Mech. 772, 107 (2015).10.1017/jfm.2015.173Google Scholar
20.Xu, S.X. and Ren, W.Q.: Reinitialization of the level-set functionin 3d simulation of moving contact lines. Commun. Comput. Phys. 20, 1163 (2016).10.4208/cicp.210815.180316aGoogle Scholar
21.Zhang, Z. and Ren, W.Q.: Simulation of moving contact lines in two-phase polymeric fluids. Comput. Math. Appl. 72, 1002 (2016).10.1016/j.camwa.2016.06.016Google Scholar
22.Martys, N.S. and Chen, H.D.: Simulation of multicomponent fluids in complex three-dimensional geometries by the lattice Boltzmann method. Phys. Rev. E 53, 743 (1996).10.1103/PhysRevE.53.743Google Scholar
23.Chen, L., Kang, Q.J., Mu, Y.T., He, Y.L., and Tao, W.Q.: A critical review of the pseudopotential multiphase lattice Boltzmann model: Methods and applications. Int. J. Heat Mass Transfer 76, 210 (2014).10.1016/j.ijheatmasstransfer.2014.04.032Google Scholar
24.Fernandes, H.C.M., Vainstein, M.H., and Brito, C.: Modeling of droplet evaporation on superhydrophobic surfaces. Langmuir 31, 7652 (2015).10.1021/acs.langmuir.5b01265Google Scholar
25.Yu, Z. and Fan, L.S.: Multirelaxation-time interaction-potential-based lattice Boltzmann model for two-phase flow. Phys. Rev. E 82, 046708 (2010).10.1103/PhysRevE.82.046708Google Scholar
26.Tartakovsky, A. and Meakin, P.: Modeling of surface tension and contact angles with smoothed particle hydrodynamics. Phys. Rev. E 72, 026301 (2005).10.1103/PhysRevE.72.026301Google Scholar
27.Kong, B. and Yang, X.Z.: Dissipative particle dynamics simulation of contact angle hysteresis on a patterned solid/air composite surface. Langmuir 22, 2065 (2006).10.1021/la051983mGoogle Scholar
28.Kasiteropoulou, D., Karakasidis, T.E., and Liakopoulos, A.: Mesoscopic simulation of fluid flow in periodically grooved microchannels. Comput. Fluids 74, 91 (2013).10.1016/j.compfluid.2013.01.010Google Scholar
29.Yao, C.W., Garvin, T.P., Alvarado, J.L., Jacobi, A.M., Jones, B.G., and Marsh, C.P.: Droplet contact angle behavior on a hybrid surface with hydrophobic and hydrophilic properties. Appl. Phys. Lett. 101, 111605 (2012).10.1063/1.4752470Google Scholar
30.Jasak, H. and Weller, H.G.: Interface Tracking Capabilities of the Inter-Gamma Differencing Scheme (Technical Report. Imperial College, University of London, London, UK, 1995).Google Scholar
Supplementary material: File

Azimi et al. supplementary material

Azimi et al. supplementary material 1

Download Azimi et al. supplementary material(File)
File 11.4 MB