Research Article
INTERMEDIATE SUMS ON POLYHEDRA: COMPUTATION AND REAL EHRHART THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 05 September 2012, pp. 1-22
-
- Article
- Export citation
ON A STRONG VERSION OF THE KEPLER CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2012, pp. 23-30
-
- Article
-
- You have access
- Export citation
ON MULTIPLICATIVELY BADLY APPROXIMABLE NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 12 June 2012, pp. 31-55
-
- Article
- Export citation
A NOTE ON THE HAUSDORFF DIMENSION OF SOME LIMINF SETS APPEARING IN SIMULTANEOUS DIOPHANTINE APPROXIMATION
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2012, pp. 56-64
-
- Article
- Export citation
ON THE DIOPHANTINE PROPERTIES OF λ-EXPANSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2012, pp. 65-86
-
- Article
- Export citation
THE RESONANCE METHOD FOR LARGE CHARACTER SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 11 September 2012, pp. 87-118
-
- Article
- Export citation
CONTINUOUS LOWER BOUNDS FOR MOMENTS OF ZETA AND L-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 15 November 2012, pp. 119-128
-
- Article
- Export citation
THE MONTGOMERY–HOOLEY THEOREM IN SHORT INTERVALS
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2012, pp. 129-139
-
- Article
- Export citation
SINGULAR SCHRÖDINGER OPERATORS IN ONE DIMENSION
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2012, pp. 141-159
-
- Article
- Export citation
L1-SMOOTHING FOR THE ORNSTEIN–UHLENBECK SEMIGROUP
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2012, pp. 160-168
-
- Article
- Export citation
REPRESENTATION THEOREMS FOR INDEFINITE QUADRATIC FORMS REVISITED
- Part of:
-
- Published online by Cambridge University Press:
- 12 June 2012, pp. 169-189
-
- Article
- Export citation
ESTIMATES OF GENERALIZED EIGENVECTORS OF HERMITIAN JACOBI MATRICES WITH A GAP IN THE ESSENTIAL SPECTRUM
- Part of:
-
- Published online by Cambridge University Press:
- 14 May 2012, pp. 191-212
-
- Article
- Export citation
NON-UNIQUENESS OF CONVEX BODIES WITH PRESCRIBED VOLUMES OF SECTIONS AND PROJECTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2012, pp. 213-221
-
- Article
- Export citation
NEIGHBORLINESS OF THE SYMMETRIC MOMENT CURVE
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2012, pp. 223-249
-
- Article
- Export citation
ON A THEOREM OF ARVANITAKIS
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2012, pp. 250-256
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
MTK VOLUME 59 ISSUE 1 COVER AND FRONT MATTER
-
- Published online by Cambridge University Press:
- 10 January 2013, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
MTK VOLUME 59 ISSUE 1 COVER AND BACK MATTER
-
- Published online by Cambridge University Press:
- 10 January 2013, pp. b1-b3
-
- Article
-
- You have access
- Export citation




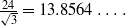
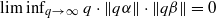 for all (
for all (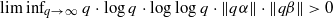 is of full dimension.
is of full dimension.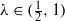 and
and 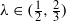 , the upper bound of
, the upper bound of