Hostname: page-component-77c89778f8-n9wrp Total loading time: 0 Render date: 2024-07-20T22:43:03.887Z Has data issue: false hasContentIssue false
  • English
  • Français

A sharp inequality of Halász type for the mean value of a multiplicative arithmetic function

Part of: Multiplicative number theory

Published online by Cambridge University Press:  26 February 2010

R. R. Hall
R. R. Hall
Affiliation:
Department of Mathematics, University of York, York YO1 5DD, England.
Get access

Extract

Let g(n) be a complex valued multiplicative function such that |g(n)| ≤ 1. In this paper we shall be concerned with the validity of the inequality

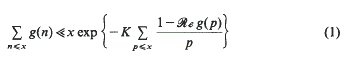
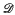under the weak condition g(p)∈ for all primes p, where 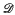is a fixed subset of the closed unit disc 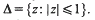Thus our point of view is similar to that of Halász [Hz 2] in that we seek a general inequality in terms of simple quantities, albeit g(p) may have a quite irregular distribution. We are not concerned here with the problem of asymptotic formulae for the sum on the left of (1) studied by (among others) Delange [D], Halász [Hz 1] and Wirsing [W].

MSC classification

Secondary: 11N37: Asymptotic results on arithmetic functions
Type
Research Article
Information
Mathematika , Volume 42 , Issue 1 , June 1995 , pp. 144 - 157
Copyright
Copyright © University College London 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BF.Bonnesen, T. and Fenchel, W.. Theorie der Konvexen Körper (Chelsea, New York, 1948).Google Scholar
D.Delange, H.. Sur les fonctions arithmétiques multiplicatives. Ann. Sci. Ec. Norm. Sup., 78 (1961), 273–304.CrossRefGoogle Scholar
E.Elliott, P. D. T. A.. Some remarks about multiplicative functions of modulus ≤ 1. In Analytic Number Theory (eds. Berndt, B. C.Diamond, H. G.Halberstam, H. and Hildebrand, A.), Progress in Math. 85 (Birkhauser, 1990), 159–164.CrossRefGoogle Scholar
Hz 1.Halasz, G.. Über die Mittelwerte multipikativer zahlentheoretischer Funktionen, Acta. Math. Acad. Sci. Hungar., 19 (1968), 365–403.CrossRefGoogle Scholar
Hz 2.Halasz, G.. On the distribution of additive and the mean values of multiplicative arithmetic functions. Studia Sci. Math. Hungar., 6 (1971), 211–233.Google Scholar
HR.Halberstam, H. and Richert, H.-E.. On a result of R. R. Hall. J. Number Theory, 11 (1979), 76–89.CrossRefGoogle Scholar
H1.Hall, R. R.. Halving an estimate obtained from Sellberg's upper bound method. Acta. Arith., 25 (1974), 347–351.CrossRefGoogle Scholar
HT 1.Hall, R. R. and Tenenbaum, G.. Divisors. Cambridge Tracts in Mathematics 90 (Cambridge University Press, 1988).CrossRefGoogle Scholar
HT 2.Hall, R. R. and Tenenbaum, G.. Effective mean value estimates for complex multiplicative functions. Math. Proc. Cam. Phil. Soc., 110 (1991), 337–351.CrossRefGoogle Scholar
Hd 1.Hildebrand, A.. Quantitative mean-value theorems for non-negative multiplicative functions 1. J. London Math. Soc., 30 (1984), 394–406.CrossRefGoogle Scholar
Hd 2.Hildebrand, A.. Quantitative mean-value theorems for non-negative multiplicative functions 2. Acta Arith., 48 (1987), 209–260.CrossRefGoogle Scholar
Mi.Minkowski, H.. Theorie der konvexen Körper, insbesondere Bergründung ihres Oberflächenbergriffs. In Gesammelte Abhandlungen (Chelsea, New York, 1967).Google Scholar
My.Montgomery, H. L.. A note on the mean values of multiplicative functions. Inst. Mittag Leffler, report no. 17 (1978).Google Scholar
T.Tenenbaum, G.. Introduction à la Theorie Analytique et Probabiliste des Nombres (Institut Elie Cartan 13, Nancy, 1990).Google Scholar
W.Wirsing, E.. Das asymptotische Verhalten von Summen über multiplikative Funktionen II. Acta. Math. Acad. Sci. Hungar., 18 (1967), 411–467.CrossRefGoogle Scholar