Hostname: page-component-76fb5796d-9pm4c Total loading time: 0 Render date: 2024-04-27T16:37:50.923Z Has data issue: false hasContentIssue false
  • English
  • Français

Exponential Squared Integrability of the Discrepancy Function in Two Dimensions

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Harmonic analysis in one variable

Published online by Cambridge University Press:  21 December 2009

Dmitriy Bilyk ,
Michael T. Lacey ,
Ioannis Parissis  and
Armen Vagharshakyan
Dmitriy Bilyk
Affiliation:
School of Mathematics, Institute for Advanced Study, Princeton, NJ 08540, U.S.A., E-mail: bilyk@math.ias.edu
Michael T. Lacey
Affiliation:
School of Mathematics, Georgia Institute of Technology, Atlanta GA 30332, U.S.A., E-mail: lacey@math.gatech.edu
Ioannis Parissis
Affiliation:
Institutionen för Matematik, Kungliga Tekniska Högskolan, SE 100 44, Stockholm, Sweden, E-mail: ioannis.parissis@gmail.com
Armen Vagharshakyan
Affiliation:
School of Mathematics, Georgia Institute of Technology, Atlanta, GA 30332, U.S.A., E-mail: armenv@math.gatech.edu
Get access

Abstract

Let AN be an N-point set in the unit square and consider the discrepancy function

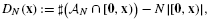
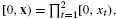where x = (x1, x2) ∈ [0,1;]2, and |[0, x)]| denotes the Lebesgue measure of the rectangle. We give various refinements of a well-known result of Schmidt [Irregularities of distribution. VII. Acta Arith. 21 (1972), 45–50] on the L∞ norm of DN. We show that necessarily

The case of α = ∞ is the Theorem of Schmidt. This estimate is sharp. For the digit-scrambled van der Corput sequence, we have

whenever N = 2n for some positive integer n. This estimate depends upon variants of the Chang–Wilson–Wolff inequality [S.-Y. A. Chang, J. M. Wilson and T. H.Wolff, Some weighted norm inequalities concerning the Schrödinger operators. Comment. Math. Helv.60(2) (1985), 217–246]. We also provide similar estimates for the BMO norm of DN.

MSC classification

Secondary: 11K38: Irregularities of distribution, discrepancy 42A05: Trigonometric polynomials, inequalities, extremal problems
Type
Research Article
Information
Mathematika , Volume 55 , Issue 1-2 , December 2009 , pp. 1 - 27
Copyright
Copyright © University College London 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Beck, J., A two-dimensional van Aardenne-Ehrenfest theorem in irregularities of distribution. Compositio. Math. 72(3) (1989), 269–339.Google Scholar
2.Beck, J. and Chen, W. W. L., Irregularities of Distribution (Cambridge Tracts in Mathematics 89), Cambridge University Press (Cambridge, 1987), xiv+294.Google Scholar
3.Bilyk, D. and Lacey, M. T., On the small ball inequality in three dimensions. Duke Math. J. 143(1) (2008), 81–115, arXiv:math.CA/060981d.Google Scholar
4.Bilyk, D., Lacey, M. T. and Vagharshakyan, A., On the small ball inequality in all dimensions. J. Funct. Anal. 254(9) (2008), 2470–2502, arXiv:0705.4619.Google Scholar
5.Chang, S.-Y. A. and Fefferman, R., A continuous version of duality of H 1 with BMO on the bidisc. Ann. of Math. (2) 112(1) (1980), 179–201.CrossRefGoogle Scholar
6.Chang, S.-Y. A. and Fefferman, R., Some recent developments in Fourier analysis and Hp-theory on product domains. Bull. Amer. Math. Soc. (N.S.) 12(1) (1985), 1–43.CrossRefGoogle Scholar
7.Chang, S.-Y. A., Wilson, J. M. and Wolff, T. H., Some weighted norm inequalities concerning the Schrödinger operators. Comment. Math. Helv. 60(2) (1985), 217–246.Google Scholar
8.Chen, W. W. L., On irregularities of distribution. Mathematika 27(2) (1980), 153–170 (1981).CrossRefGoogle Scholar
9.Chen, W. W. L., On irregularities of distribution. II. Quart. J. Math. Oxford Ser. (2) 34(135) (1983), 257–279.Google Scholar
10.Dunker, T., Kühn, T., Mikhail, L. and Werner, L., Metric entropy of the integration operator and small ball probabilities for the Brownian sheet. C. R. Acad. Sci. Paris Sér. I Math. 326(3) (1998), 347–352 (English, with English and French summaries).Google Scholar
11.Fefferman, R. and Pipher, J., Multiparameter operators and sharp weighted inequalities. Amer. J. Math. 119(2) (1997), 337–369.CrossRefGoogle Scholar
12., G. Halász, On Roth's method in the theory of irregularities of point distributions. In Recent Progress in Analytic Number Theory, (Durham, 1979) Vol. 2, Academic Press (London, 1981), 79–94.Google Scholar
13.Halton, J. H. and , Z. S. K., The extreme and L 2 discrepancies of some plane sets. Monatsh. Math. 73 (1969), 316–328.Google Scholar
14.Kritzer, P. and Pillichshammer, F., An exact formula for the L 2 discrepancy of the shifted Hammersley point set. Uniform Distribution Theory 1(1) (2006), 1–13.Google Scholar
15.Lacey, M. T., On the discrepancy function in arbitrary dimension, close to L 1. Anal. Math. 34(2) (2008), 119–136.Google Scholar
16.Lindenstrauss, J. and Tzafriri, L., Classical Banach Spaces. I (Sequence spaces; Ergebnisse der Mathematik und ihrer Grenzgebiete 92), Springer (Berlin, 1977), xiii+188.Google Scholar
17.Matoušek, J., Geometric Discrepancy (Algorithms and Combinatorics 18), Springer (Berlin, 1999).Google Scholar
18.Pipher, J., Bounded double square functions. Ann. Inst. Fourier (Grenoble) 36(2) (1986), 69–82 (English, with French summary).CrossRefGoogle Scholar
19.Pipher, J. and Ward, L. A., BMO from dyadic BMO on the bidisc. J. London Math. Soc. (2) 77(2) (2008), 524–544.Google Scholar
20.Roth, K. F., On irregularities of distribution. Mathematika 1 (1954), 73–79.CrossRefGoogle Scholar
21.Schmidt, W. M., Irregularities of distribution. VII. Acta Arith. 21 (1972), 45–50.Google Scholar
22.Schmidt, W. M., Lectures on Irregularities of Distribution (Tata Institute of Fundamental Research Lectures on Mathematics and Physics 56), Tata Institute of Fundamental Research (Bombay, 1977a), v+128.Google Scholar
23.Schmidt, W. M., Irregularities of distribution. X. In Number Theory and Algebra, Academic Press (New York, 1977b), 311–329.Google Scholar
24.Talagrand, M., The small ball problem for the Brownian sheet. Ann. Probab. 22(3) (1994), 1331–1354.CrossRefGoogle Scholar
25.Temlyakov, V. N., An inequality for trigonometric polynomials and its application for estimating the entropy numbers. J. Complexity 11(2) (1995), 293–307.CrossRefGoogle Scholar
26.Treil, S., H 1 and dyadic H 1. (2008), http://arxiv.org/abs/0809.3288.Google Scholar
27.Corput, J. G. van der, Verteilungsfunktionen I. Akad.Wetensch. Amsterdam Proc. 38 (1935), 813–821.Google Scholar
28.Wang, G., Sharp square-function inequalities for conditionally symmetric martingales. Trans. Amer. Math. Soc. 328(1) (1991), 393–419.CrossRefGoogle Scholar