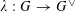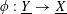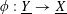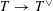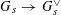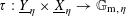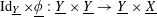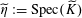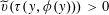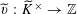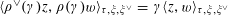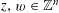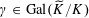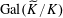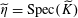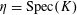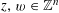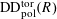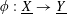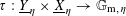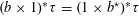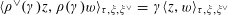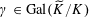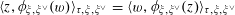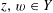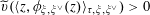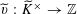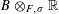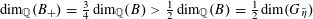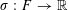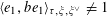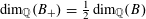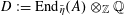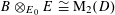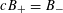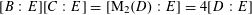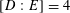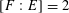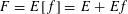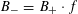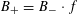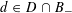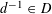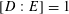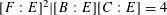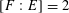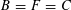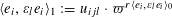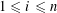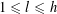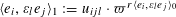1 Introduction
We start with a well-known example, the Dwork family of elliptic curves
 $$\begin{eqnarray}X^{3}+Y^{3}+Z^{3}-3tXYZ=0\end{eqnarray}$$
$$\begin{eqnarray}X^{3}+Y^{3}+Z^{3}-3tXYZ=0\end{eqnarray}$$
over the projective line
![]() $\mathbb{P}_{\mathbb{Q}}^{1}$
over
$\mathbb{P}_{\mathbb{Q}}^{1}$
over
![]() $\mathbb{Q}$
, where
$\mathbb{Q}$
, where
![]() $t$
is the affine coordinate, with the identity section given by the point at infinity
$t$
is the affine coordinate, with the identity section given by the point at infinity
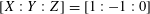 $[X:Y:Z]=[1:-1:0]$
. It also doubles as the modular curve of level
$[X:Y:Z]=[1:-1:0]$
. It also doubles as the modular curve of level
![]() $3$
.
$3$
.
It has bad, semistable reduction at
![]() $t=\infty$
and the third roots of unity. The corresponding Néron model has the split torus as the identity component of the fiber at
$t=\infty$
and the third roots of unity. The corresponding Néron model has the split torus as the identity component of the fiber at
![]() $t=\infty$
(because the equation becomes
$t=\infty$
(because the equation becomes
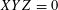 $XYZ=0$
), but at
$XYZ=0$
), but at
![]() $t=1$
we get a non-split torus
$t=1$
we get a non-split torus
![]() $T$
that sits in the short exact sequence
$T$
that sits in the short exact sequence

where
![]() $\operatorname{Norm}$
denotes the norm homomorphism of the quadratic extension
$\operatorname{Norm}$
denotes the norm homomorphism of the quadratic extension
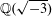 $\mathbb{Q}(\sqrt{-3})$
over
$\mathbb{Q}(\sqrt{-3})$
over
![]() $\mathbb{Q}$
. This leads to the following natural question.
$\mathbb{Q}$
. This leads to the following natural question.
Question 1.1. To which algebraic tori can abelian varieties degenerate?
However, this question turns out to be a bit naive, in the sense that it allows an answer that is somewhat shallow. Indeed, as we shall explain in the main text with more details, the question can be rather easily reduced to the case of the split one-dimensional torus
![]() $\mathbb{G}_{\text{m}}$
by finite étale descent, where an affirmative answer is provided by the classical theory of Tate curves. The generic abelian variety obtained this way will be geometrically the
$\mathbb{G}_{\text{m}}$
by finite étale descent, where an affirmative answer is provided by the classical theory of Tate curves. The generic abelian variety obtained this way will be geometrically the
![]() $n$
-fold product of an elliptic curve without CM (complex multiplication), where
$n$
-fold product of an elliptic curve without CM (complex multiplication), where
![]() $n$
is the dimension of the torus.
$n$
is the dimension of the torus.
A better and deeper question is the following.
Question 1.2. To which algebraic tori can absolutely simple abelian varieties degenerate?
Here, as usual, an abelian variety is called absolutely simple if its base change to an algebraic closure of the base field is not isogenous to a non-trivial product of abelian varieties of smaller dimensions.
For the distinction between Questions 1.1 and 1.2, an apt analogy can be made with complex moduli of abelian varieties. To a simple algebra
![]() $B$
with involution of types I–IV and a fixed complex representation of
$B$
with involution of types I–IV and a fixed complex representation of
![]() $B$
, one attaches the moduli of polarized abelian varieties with endomorphisms of the given type. One expects, and can prove in most cases, that a very general member in the moduli has an endomorphism algebra no bigger than
$B$
, one attaches the moduli of polarized abelian varieties with endomorphisms of the given type. One expects, and can prove in most cases, that a very general member in the moduli has an endomorphism algebra no bigger than
![]() $B$
; the rough idea is that those abelian varieties with more endomorphisms than prescribed should form a “thin” or nowhere dense subset. However, a careful proof is necessary, as there are exceptional cases where a very general member is not even simple (see [Reference Shimura20, §4, Theorem 5 and Propositions 14, 15, 17, 18, and 19] or [Reference Birkenhake and Lange2, Theorem 9.9.1]).
$B$
; the rough idea is that those abelian varieties with more endomorphisms than prescribed should form a “thin” or nowhere dense subset. However, a careful proof is necessary, as there are exceptional cases where a very general member is not even simple (see [Reference Shimura20, §4, Theorem 5 and Propositions 14, 15, 17, 18, and 19] or [Reference Birkenhake and Lange2, Theorem 9.9.1]).
Our main theorem answers Question 1.2, in the affirmative, for all algebraic tori over all base fields.
Theorem 1.3. Let
![]() $T$
be any algebraic torus over any base field
$T$
be any algebraic torus over any base field
![]() $k$
. Then there exists a semi-abelian scheme
$k$
. Then there exists a semi-abelian scheme
![]() $G$
over a noetherian normal base scheme
$G$
over a noetherian normal base scheme
![]() $S$
with a
$S$
with a
![]() $k$
-valued closed point
$k$
-valued closed point
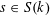 $s\in S(k)$
generalizing to a generic point
$s\in S(k)$
generalizing to a generic point
![]() $\unicode[STIX]{x1D702}$
such that the following hold.
$\unicode[STIX]{x1D702}$
such that the following hold.
(1) The special fiber
 $G_{s}$
is isomorphic to
$G_{s}$
is isomorphic to
 $T$
over
$T$
over
 $k$
.
$k$
.(2) The generic fiber
 $G_{\unicode[STIX]{x1D702}}$
is an absolutely simple abelian variety.
$G_{\unicode[STIX]{x1D702}}$
is an absolutely simple abelian variety.
More precisely, we may take
![]() $S$
to be of one of the following three kinds of Dedekind schemes:
$S$
to be of one of the following three kinds of Dedekind schemes:
(a) the spectrum of any complete discrete valuation ring, which can be freely prescribed (independent of
 $T$
), with residue field
$T$
), with residue field
 $k$
;
$k$
;(b) a certain connected smooth curve over
 $k$
(depending on
$k$
(depending on
 $T$
) with a
$T$
) with a
 $k$
-valued point
$k$
-valued point
 $s$
; and
$s$
; and(c) (when
 $k$
is a finite field) a certain “arithmetic curve” (depending on
$k$
is a finite field) a certain “arithmetic curve” (depending on
 $T$
), i.e. an open subset of the spectrum of some number ring, with a closed point
$T$
), i.e. an open subset of the spectrum of some number ring, with a closed point
 $s$
corresponding to an unramified prime ideal with residue field
$s$
corresponding to an unramified prime ideal with residue field
 $k$
.
$k$
.
In case
![]() $T$
has dimension one, we can exhibit the desired semi-abelian schemes
$T$
has dimension one, we can exhibit the desired semi-abelian schemes
![]() $G$
over Dedekind
$G$
over Dedekind
![]() $S$
for each non-split torus
$S$
for each non-split torus
![]() $T$
explicitly. Such tori are classified by the separable quadratic extensions of
$T$
explicitly. Such tori are classified by the separable quadratic extensions of
![]() $k$
, and we can write down suitable Weierstraß equations with special fibre
$k$
, and we can write down suitable Weierstraß equations with special fibre
![]() $T$
. (The generic absolute simpleness is automatic in dimension one.)
$T$
. (The generic absolute simpleness is automatic in dimension one.)
However, in dimensions
![]() $n\geqslant 2$
(already for
$n\geqslant 2$
(already for
![]() $n=2$
), we quickly lose explicit control on both sides. The isomorphism classes of
$n=2$
), we quickly lose explicit control on both sides. The isomorphism classes of
![]() $n$
-dimensional tori over
$n$
-dimensional tori over
![]() $k$
are in one-to-one correspondence with the isomorphism classes of continuous representations
$k$
are in one-to-one correspondence with the isomorphism classes of continuous representations
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}:\operatorname{Gal}(k^{s}/k)\rightarrow \operatorname{GL}_{n}(\mathbb{Z}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}:\operatorname{Gal}(k^{s}/k)\rightarrow \operatorname{GL}_{n}(\mathbb{Z}),\end{eqnarray}$$
where
![]() $k^{s}$
denotes any separable closure of
$k^{s}$
denotes any separable closure of
![]() $k$
, on the discrete module
$k$
, on the discrete module
![]() $\mathbb{Z}^{n}$
(corresponding to the Galois actions on the character groups of the tori), and it seems hopeless to classify them completely. On the other side, we do not have a good way of writing down families of general abelian varieties using explicit equations. In order to solve the problem, we use the theory of degeneration of polarized semi-abelian schemes (as in [Reference Mumford18], [Reference Faltings and Chai7, Chs II and III], and [Reference Lan14, Ch. 4]).
$\mathbb{Z}^{n}$
(corresponding to the Galois actions on the character groups of the tori), and it seems hopeless to classify them completely. On the other side, we do not have a good way of writing down families of general abelian varieties using explicit equations. In order to solve the problem, we use the theory of degeneration of polarized semi-abelian schemes (as in [Reference Mumford18], [Reference Faltings and Chai7, Chs II and III], and [Reference Lan14, Ch. 4]).
After the main theorem, it is natural to ask a similar question with the additional condition that the (absolutely simple) generic abelian variety should be equipped with non-trivial endomorphisms. (Such endomorphism structures then necessarily and uniquely extend to the whole semi-abelian scheme; see [Reference Raynaud19, IX, 1.4], [Reference Faltings and Chai7, Ch. I, Proposition 2.7], or [Reference Lan14, Proposition 3.3.1.5].) We will also answer this question, with an affirmative answer similar to Theorem 1.3 (except in two special cases).
We note, however, that Question 1.2 and its analogue as in the last paragraph are not about the fibers of the tautological semi-abelian schemes carried by the toroidal compactifications of the Siegel moduli stacks or more general PEL moduli problems constructed in [Reference Faltings and Chai7, Ch. IV] and [Reference Lan14, Ch. 6], because only split tori are used (and needed in the valuative criterion for properness) in the constructions there. Nevertheless, our use of the theory of degeneration is inspired by such constructions.
Here is an outline of the article. In §2, we construct explicit families for one-dimensional tori. In §3, we review some basic facts about the descent data for tori, and give the above-mentioned explanation why Question 1.1 is a bit too naive. To attack Question 1.2 in general, we recall relevant facts from the theory of degeneration in §4. Using this theory, we give the proof of Theorem 1.3 in §§5 and 6. Finally, in §7, we turn to the conditions for tori to be realizable as the degeneration of absolutely simple abelian varieties with non-trivial endomorphisms.
2 One-dimensional case
Let
![]() $T$
be an algebraic torus of dimension one over a field
$T$
be an algebraic torus of dimension one over a field
![]() $k$
. Let us fix the choice of a separable closure
$k$
. Let us fix the choice of a separable closure
![]() $k^{s}$
of
$k^{s}$
of
![]() $k$
. Then the action of the Galois group
$k$
. Then the action of the Galois group
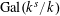 $\operatorname{Gal}(k^{s}/k)$
on the character group
$\operatorname{Gal}(k^{s}/k)$
on the character group
 $X^{\ast }(T)\cong \mathbb{Z}$
of
$X^{\ast }(T)\cong \mathbb{Z}$
of
![]() $T$
is either trivial (in which case
$T$
is either trivial (in which case
![]() $T$
is split), or surjects onto
$T$
is split), or surjects onto
![]() $\{\pm 1\}$
, corresponding to a separable quadratic extension
$\{\pm 1\}$
, corresponding to a separable quadratic extension
![]() $\widetilde{k}$
of
$\widetilde{k}$
of
![]() $k$
in
$k$
in
![]() $k^{s}$
.
$k^{s}$
.
Let
![]() $R$
be any Dedekind domain and
$R$
be any Dedekind domain and
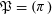 $\mathfrak{P}=(\unicode[STIX]{x1D70B})$
a principal maximal ideal of
$\mathfrak{P}=(\unicode[STIX]{x1D70B})$
a principal maximal ideal of
![]() $R$
with residue field
$R$
with residue field
![]() $k$
. (For example,
$k$
. (For example,
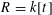 $R=k[t]$
and
$R=k[t]$
and
![]() $\mathfrak{P}=(t)$
.)
$\mathfrak{P}=(t)$
.)
Proposition 2.1. Suppose that
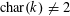 $\operatorname{char}(k)\neq 2$
, and write
$\operatorname{char}(k)\neq 2$
, and write
 $\widetilde{k}=k(\sqrt{b})$
, where
$\widetilde{k}=k(\sqrt{b})$
, where
![]() $b\in k$
is a non-square element. Then for any lift
$b\in k$
is a non-square element. Then for any lift
![]() $\mathfrak{b}\in R$
of
$\mathfrak{b}\in R$
of
![]() $b$
, the Weierstraß equation
$b$
, the Weierstraß equation
 $$\begin{eqnarray}Y^{2}Z=X^{3}+\mathfrak{b}X^{2}Z+\unicode[STIX]{x1D70B}Z^{3}\end{eqnarray}$$
$$\begin{eqnarray}Y^{2}Z=X^{3}+\mathfrak{b}X^{2}Z+\unicode[STIX]{x1D70B}Z^{3}\end{eqnarray}$$
over
![]() $\operatorname{Spec}(R)$
defines an elliptic curve over the fraction field of
$\operatorname{Spec}(R)$
defines an elliptic curve over the fraction field of
![]() $R$
, has semistable reduction at
$R$
, has semistable reduction at
![]() $\mathfrak{P}$
, and the fiber of the Néron model at
$\mathfrak{P}$
, and the fiber of the Néron model at
![]() $\mathfrak{P}$
is the
$\mathfrak{P}$
is the
![]() $k$
-torus on whose character group
$k$
-torus on whose character group
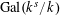 $\operatorname{Gal}(k^{s}/k)$
acts via the quadratic character of
$\operatorname{Gal}(k^{s}/k)$
acts via the quadratic character of
![]() $\widetilde{k}/k$
.
$\widetilde{k}/k$
.
Proof. The discriminant of the Weierstraß equation (see [Reference Tate21, p. 180]) is given by
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}=(-16\unicode[STIX]{x1D70B})(4\mathfrak{b}^{3}+27\unicode[STIX]{x1D70B}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}=(-16\unicode[STIX]{x1D70B})(4\mathfrak{b}^{3}+27\unicode[STIX]{x1D70B}).\end{eqnarray}$$
This is non-zero, and is in fact a uniformizer, in
![]() $R_{\mathfrak{P}}$
, since
$R_{\mathfrak{P}}$
, since
![]() $2$
is a unit in
$2$
is a unit in
![]() $R_{\mathfrak{P}}$
; hence the first assertion.
$R_{\mathfrak{P}}$
; hence the first assertion.
Let
![]() $C$
denote the singular curve at
$C$
denote the singular curve at
![]() $\mathfrak{P}$
:
$\mathfrak{P}$
:
 $$\begin{eqnarray}Y^{2}Z=X^{3}+bX^{2}Z.\end{eqnarray}$$
$$\begin{eqnarray}Y^{2}Z=X^{3}+bX^{2}Z.\end{eqnarray}$$
The complement of the unique singular point
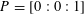 $P=[0:0:1]$
in
$P=[0:0:1]$
in
![]() $C$
is the fiber of the Néron model. We know that it is a one-dimensional torus, and that it splits over
$C$
is the fiber of the Néron model. We know that it is a one-dimensional torus, and that it splits over
![]() $\widetilde{k}$
. Therefore, it is enough to show that it is not split over
$\widetilde{k}$
. Therefore, it is enough to show that it is not split over
![]() $k$
.
$k$
.
Let
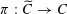 $\unicode[STIX]{x1D70B}:\widetilde{C}\rightarrow C$
be the blowup of
$\unicode[STIX]{x1D70B}:\widetilde{C}\rightarrow C$
be the blowup of
![]() $C$
at
$C$
at
![]() $P$
, which induces an isomorphism
$P$
, which induces an isomorphism
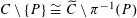 $C\setminus \{P\}\cong \widetilde{C}\setminus \unicode[STIX]{x1D70B}^{-1}(P)$
. Because the slopes of the tangent cone
$C\setminus \{P\}\cong \widetilde{C}\setminus \unicode[STIX]{x1D70B}^{-1}(P)$
. Because the slopes of the tangent cone
 $$\begin{eqnarray}y^{2}=bx^{2}\end{eqnarray}$$
$$\begin{eqnarray}y^{2}=bx^{2}\end{eqnarray}$$
to
![]() $C$
at
$C$
at
![]() $P$
are
$P$
are
![]() $\pm \sqrt{b}$
, which are not contained in
$\pm \sqrt{b}$
, which are not contained in
![]() $k$
, the inverse image
$k$
, the inverse image
![]() $\unicode[STIX]{x1D70B}^{-1}(P)$
consists of one point of degree
$\unicode[STIX]{x1D70B}^{-1}(P)$
consists of one point of degree
![]() $2$
on
$2$
on
![]() $\widetilde{C}$
. If
$\widetilde{C}$
. If
![]() $C\setminus \{P\}$
were split over
$C\setminus \{P\}$
were split over
![]() $k$
, this would not happen.◻
$k$
, this would not happen.◻
Proposition 2.2. Suppose that
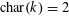 $\operatorname{char}(k)=2$
, and
$\operatorname{char}(k)=2$
, and
![]() $\widetilde{k}$
be a separable quadratic extension of
$\widetilde{k}$
be a separable quadratic extension of
![]() $k$
. Write
$k$
. Write
![]() $\widetilde{k}$
as the Artin–Schreier extension
$\widetilde{k}$
as the Artin–Schreier extension
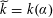 $\widetilde{k}=k(\unicode[STIX]{x1D6FC})$
, where
$\widetilde{k}=k(\unicode[STIX]{x1D6FC})$
, where
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}+b=0,\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}^{2}+\unicode[STIX]{x1D6FC}+b=0,\end{eqnarray}$$
and
![]() $b\in k$
. Then for any lift
$b\in k$
. Then for any lift
![]() $\mathfrak{b}\in R$
of
$\mathfrak{b}\in R$
of
![]() $b$
, the Weierstraß equation
$b$
, the Weierstraß equation
 $$\begin{eqnarray}Y^{2}Z+XYZ=X^{3}+\mathfrak{b}X^{2}Z+\unicode[STIX]{x1D70B}Z^{3}\end{eqnarray}$$
$$\begin{eqnarray}Y^{2}Z+XYZ=X^{3}+\mathfrak{b}X^{2}Z+\unicode[STIX]{x1D70B}Z^{3}\end{eqnarray}$$
over
![]() $\operatorname{Spec}(R)$
defines an elliptic curve over the fraction field of
$\operatorname{Spec}(R)$
defines an elliptic curve over the fraction field of
![]() $R$
, has semistable reduction at
$R$
, has semistable reduction at
![]() $\mathfrak{P}$
, and the fiber of the Néron model at
$\mathfrak{P}$
, and the fiber of the Néron model at
![]() $\mathfrak{P}$
is the
$\mathfrak{P}$
is the
![]() $k$
-torus on whose character group
$k$
-torus on whose character group
 $\operatorname{Gal}(k^{s}/k)$
acts via the quadratic character of
$\operatorname{Gal}(k^{s}/k)$
acts via the quadratic character of
![]() $\widetilde{k}/k$
.
$\widetilde{k}/k$
.
Proof. The proof is parallel. We only note that the discriminant
 $$\begin{eqnarray}\unicode[STIX]{x1D6E5}=-(1+4\mathfrak{b})^{3}\unicode[STIX]{x1D70B}-16\cdot 27\unicode[STIX]{x1D70B}^{2}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E5}=-(1+4\mathfrak{b})^{3}\unicode[STIX]{x1D70B}-16\cdot 27\unicode[STIX]{x1D70B}^{2}\end{eqnarray}$$
is again a uniformizer in
![]() $R_{\mathfrak{P}}$
, this time because
$R_{\mathfrak{P}}$
, this time because
![]() $2$
is in
$2$
is in
![]() $\mathfrak{P}$
.◻
$\mathfrak{P}$
.◻
3 Descent data for tori
In this section, we review some basic facts about the descent data for tori. At the end of this section, we explain that the rather naive Question 1.1 can be easily reduced to the case of
![]() $\mathbb{G}_{\text{m}}$
, which can then be answered in the affirmative by the classical theory of Tate curves. In fact, the argument will also show that the construction of degenerating abelian varieties can be made functorial (and compatible with base field extensions) in the tori.
$\mathbb{G}_{\text{m}}$
, which can then be answered in the affirmative by the classical theory of Tate curves. In fact, the argument will also show that the construction of degenerating abelian varieties can be made functorial (and compatible with base field extensions) in the tori.
We start with the following basic fact.
Lemma 3.1. Let
![]() $R$
be a complete noetherian local ring with residue field
$R$
be a complete noetherian local ring with residue field
![]() $k$
. Then pulling back from
$k$
. Then pulling back from
![]() $R$
to
$R$
to
![]() $k$
induces an equivalence from the category of isotrivial tori over
$k$
induces an equivalence from the category of isotrivial tori over
![]() $R$
to the category of tori over
$R$
to the category of tori over
![]() $k$
. (Recall that a torus is isotrivial if it splits over a finite étale cover of its base scheme; see [Reference Demazure and Grothendieck6, IX, 1.1].)
$k$
. (Recall that a torus is isotrivial if it splits over a finite étale cover of its base scheme; see [Reference Demazure and Grothendieck6, IX, 1.1].)
Proof. This follows from [Reference Demazure and Grothendieck6, X, 3.3]. (Indeed, by [Reference Demazure and Grothendieck6, X, 2.1], all tori over
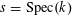 $s=\operatorname{Spec}(k)$
are isotrivial, and so the lemma is a consequence of [Reference Demazure and Grothendieck6, X, 3.2].) ◻
$s=\operatorname{Spec}(k)$
are isotrivial, and so the lemma is a consequence of [Reference Demazure and Grothendieck6, X, 3.2].) ◻
Now, suppose
![]() $R$
is any complete discrete valuation ring with residue field
$R$
is any complete discrete valuation ring with residue field
![]() $k$
and fraction field
$k$
and fraction field
![]() $K$
. Let
$K$
. Let
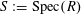 $S:=\operatorname{Spec}(R)$
,
$S:=\operatorname{Spec}(R)$
,
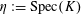 $\unicode[STIX]{x1D702}:=\operatorname{Spec}(K)$
, and
$\unicode[STIX]{x1D702}:=\operatorname{Spec}(K)$
, and
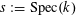 $s:=\operatorname{Spec}(k)$
. We shall denote the pullbacks to
$s:=\operatorname{Spec}(k)$
. We shall denote the pullbacks to
![]() $\unicode[STIX]{x1D702}$
or
$\unicode[STIX]{x1D702}$
or
![]() $s$
by subscripts
$s$
by subscripts
![]() $\unicode[STIX]{x1D702}$
or
$\unicode[STIX]{x1D702}$
or
![]() $s$
, respectively.
$s$
, respectively.
Suppose
![]() $T$
is an isotrivial torus over
$T$
is an isotrivial torus over
![]() $S$
. Then there exists a finite étale extension
$S$
. Then there exists a finite étale extension
![]() $\widetilde{R}$
of
$\widetilde{R}$
of
![]() $R$
, which we may and we shall assume to be a complete discrete valuation ring as well, such that
$R$
, which we may and we shall assume to be a complete discrete valuation ring as well, such that
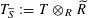 $T_{\widetilde{S}}:=T\otimes _{R}\widetilde{R}$
is a split torus over
$T_{\widetilde{S}}:=T\otimes _{R}\widetilde{R}$
is a split torus over
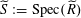 $\widetilde{S}:=\operatorname{Spec}(\widetilde{R})$
. Let
$\widetilde{S}:=\operatorname{Spec}(\widetilde{R})$
. Let
![]() $\widetilde{K}$
and
$\widetilde{K}$
and
![]() $\widetilde{k}$
denote the fraction and residue fields of
$\widetilde{k}$
denote the fraction and residue fields of
![]() $\widetilde{R}$
, respectively, and let
$\widetilde{R}$
, respectively, and let
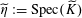 $\widetilde{\unicode[STIX]{x1D702}}:=\operatorname{Spec}(\widetilde{K})$
and
$\widetilde{\unicode[STIX]{x1D702}}:=\operatorname{Spec}(\widetilde{K})$
and
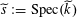 $\widetilde{s}:=\operatorname{Spec}(\widetilde{k})$
. By [Reference Grothendieck8, V, 7, and 4(g)], up to replacing
$\widetilde{s}:=\operatorname{Spec}(\widetilde{k})$
. By [Reference Grothendieck8, V, 7, and 4(g)], up to replacing
![]() $\widetilde{R}$
with a further finite étale extension, we may and we shall assume that
$\widetilde{R}$
with a further finite étale extension, we may and we shall assume that
![]() $\widetilde{K}$
is a Galois extension of
$\widetilde{K}$
is a Galois extension of
![]() $K$
. Again, we shall denote the pullbacks to
$K$
. Again, we shall denote the pullbacks to
![]() $\widetilde{\unicode[STIX]{x1D702}}$
or
$\widetilde{\unicode[STIX]{x1D702}}$
or
![]() $\widetilde{s}$
by subscripts
$\widetilde{s}$
by subscripts
![]() $\widetilde{\unicode[STIX]{x1D702}}$
or
$\widetilde{\unicode[STIX]{x1D702}}$
or
![]() $\widetilde{s}$
, respectively.
$\widetilde{s}$
, respectively.
Let
![]() $\text{}\underline{X}$
denote the character group of
$\text{}\underline{X}$
denote the character group of
![]() $T$
, which is an étale sheaf of free abelian groups of finite ranks over
$T$
, which is an étale sheaf of free abelian groups of finite ranks over
![]() $S$
. Then
$S$
. Then
![]() $\text{}\underline{X}$
is the unique étale sheaf lifting
$\text{}\underline{X}$
is the unique étale sheaf lifting
![]() $\text{}\underline{X}_{s}$
, the character group of
$\text{}\underline{X}_{s}$
, the character group of
![]() $T_{s}$
. Let
$T_{s}$
. Let
![]() $n$
denote the relative dimension of
$n$
denote the relative dimension of
![]() $T$
over
$T$
over
![]() $S$
. Then there exists some isomorphism
$S$
. Then there exists some isomorphism
 $\unicode[STIX]{x1D709}:\mathbb{Z}^{n}\stackrel{{\sim}}{\rightarrow }\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
, where we abusively denote by
$\unicode[STIX]{x1D709}:\mathbb{Z}^{n}\stackrel{{\sim}}{\rightarrow }\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
, where we abusively denote by
![]() $\mathbb{Z}^{n}$
the associated constant étale sheaf over
$\mathbb{Z}^{n}$
the associated constant étale sheaf over
![]() $\widetilde{\unicode[STIX]{x1D702}}$
, which induces a representation
$\widetilde{\unicode[STIX]{x1D702}}$
, which induces a representation
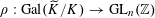 $\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
giving the descent data for the étale sheaf
$\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
giving the descent data for the étale sheaf
![]() $\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
. Since
$\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
. Since
![]() $\widetilde{R}$
is finite étale over
$\widetilde{R}$
is finite étale over
![]() $R$
, we have
$R$
, we have
 $\operatorname{Gal}(\widetilde{K}/K)\cong \operatorname{Gal}(\widetilde{k}/k)$
, and so
$\operatorname{Gal}(\widetilde{K}/K)\cong \operatorname{Gal}(\widetilde{k}/k)$
, and so
![]() $\unicode[STIX]{x1D70C}$
determines and is determined by a representation
$\unicode[STIX]{x1D70C}$
determines and is determined by a representation
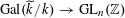 $\operatorname{Gal}(\widetilde{k}/k)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
. Since the automorphism group of any torus is canonically isomorphic to the automorphism group of the associated character group, the representation
$\operatorname{Gal}(\widetilde{k}/k)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
. Since the automorphism group of any torus is canonically isomorphic to the automorphism group of the associated character group, the representation
![]() $\unicode[STIX]{x1D70C}$
also defines the data for
$\unicode[STIX]{x1D70C}$
also defines the data for
![]() $T_{S}$
(respectively
$T_{S}$
(respectively
![]() $T_{s}$
) to descend from
$T_{s}$
) to descend from
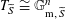 $T_{\widetilde{S}}\cong \mathbb{G}_{\text{m},\widetilde{S}}^{n}$
(respectively
$T_{\widetilde{S}}\cong \mathbb{G}_{\text{m},\widetilde{S}}^{n}$
(respectively
 $T_{\widetilde{s}}\cong \mathbb{G}_{\text{m},\widetilde{s}}^{n}$
). (See, for example, [Reference Bosch, Lütkebohmert and Raybaud3, Ch. 6, §6.2, Example B] for an explanation that descent data for schemes with respect to the finite étale base extension
$T_{\widetilde{s}}\cong \mathbb{G}_{\text{m},\widetilde{s}}^{n}$
). (See, for example, [Reference Bosch, Lütkebohmert and Raybaud3, Ch. 6, §6.2, Example B] for an explanation that descent data for schemes with respect to the finite étale base extension
![]() $R\rightarrow \widetilde{R}$
as above are equivalent to actions of the Galois group
$R\rightarrow \widetilde{R}$
as above are equivalent to actions of the Galois group
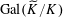 $\operatorname{Gal}(\widetilde{K}/K)$
on the schemes.)
$\operatorname{Gal}(\widetilde{K}/K)$
on the schemes.)
Conversely, any torus
![]() $T_{s}$
with character group
$T_{s}$
with character group
![]() $\text{}\underline{X}_{s}$
over
$\text{}\underline{X}_{s}$
over
![]() $s$
canonically lifts to an isotrivial torus
$s$
canonically lifts to an isotrivial torus
![]() $T$
with character group
$T$
with character group
![]() $\text{}\underline{X}$
over
$\text{}\underline{X}$
over
![]() $S$
, by Lemma 3.1. If
$S$
, by Lemma 3.1. If
![]() $T_{s}$
is of dimension
$T_{s}$
is of dimension
![]() $n$
, then we have trivializations
$n$
, then we have trivializations
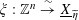 $\unicode[STIX]{x1D709}:\mathbb{Z}^{n}\stackrel{{\sim}}{\rightarrow }\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and representations
$\unicode[STIX]{x1D709}:\mathbb{Z}^{n}\stackrel{{\sim}}{\rightarrow }\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and representations
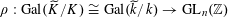 $\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\cong \operatorname{Gal}(\widetilde{k}/k)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
as above, for suitable choices of
$\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\cong \operatorname{Gal}(\widetilde{k}/k)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
as above, for suitable choices of
![]() $\widetilde{S}$
, etc.
$\widetilde{S}$
, etc.
Proposition 3.2. Suppose
![]() $G_{0}$
is a semi-abelian scheme over
$G_{0}$
is a semi-abelian scheme over
![]() $S$
with special fiber
$S$
with special fiber
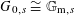 $G_{0,s}\cong \mathbb{G}_{\text{m},s}$
and with generic fiber
$G_{0,s}\cong \mathbb{G}_{\text{m},s}$
and with generic fiber
![]() $G_{0,\unicode[STIX]{x1D702}}$
an elliptic curve. Suppose
$G_{0,\unicode[STIX]{x1D702}}$
an elliptic curve. Suppose
![]() $T_{s}$
is a torus over
$T_{s}$
is a torus over
![]() $s$
, and suppose
$s$
, and suppose
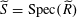 $\widetilde{S}=\operatorname{Spec}(\widetilde{R})$
, etc, are as above. Then there exists a semi-abelian scheme
$\widetilde{S}=\operatorname{Spec}(\widetilde{R})$
, etc, are as above. Then there exists a semi-abelian scheme
![]() $G$
over
$G$
over
![]() $S$
such that
$S$
such that
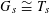 $G_{s}\cong T_{s}$
, such that
$G_{s}\cong T_{s}$
, such that
![]() $G_{\unicode[STIX]{x1D702}}$
is an abelian variety, and such that
$G_{\unicode[STIX]{x1D702}}$
is an abelian variety, and such that
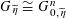 $G_{\widetilde{\unicode[STIX]{x1D702}}}\cong G_{0,\widetilde{\unicode[STIX]{x1D702}}}^{n}$
. In particular, Question 1.1 has an affirmative answer. Moreover, for a fixed choice of
$G_{\widetilde{\unicode[STIX]{x1D702}}}\cong G_{0,\widetilde{\unicode[STIX]{x1D702}}}^{n}$
. In particular, Question 1.1 has an affirmative answer. Moreover, for a fixed choice of
![]() $G_{0}$
, the assignment of
$G_{0}$
, the assignment of
![]() $G$
to
$G$
to
![]() $T_{s}$
is functorial (and compatible with base field extensions) in the torus
$T_{s}$
is functorial (and compatible with base field extensions) in the torus
![]() $T_{s}$
.
$T_{s}$
.
Proof. By [Reference Raynaud19, XI, 1.13] (see also [Reference Lan14, Remark 3.3.3.9]), any semi-abelian scheme over the noetherian normal base scheme
![]() $S$
is equipped with some relative ample invertible sheaf over
$S$
is equipped with some relative ample invertible sheaf over
![]() $S$
. By the theory of fpqc descent (as in [Reference Grothendieck8, VIII, 7.8]), all descent data for such quasi-projective semi-abelian schemes are effective. Since the representation
$S$
. By the theory of fpqc descent (as in [Reference Grothendieck8, VIII, 7.8]), all descent data for such quasi-projective semi-abelian schemes are effective. Since the representation
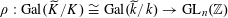 $\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\cong \operatorname{Gal}(\widetilde{k}/k)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
defining the data for
$\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\cong \operatorname{Gal}(\widetilde{k}/k)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
defining the data for
![]() $T_{S}$
to descend from
$T_{S}$
to descend from
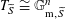 $T_{\widetilde{S}}\cong \mathbb{G}_{\text{m},\widetilde{S}}^{n}$
also defines some descent data for
$T_{\widetilde{S}}\cong \mathbb{G}_{\text{m},\widetilde{S}}^{n}$
also defines some descent data for
![]() $G_{0,\widetilde{S}}^{n}$
, which are effective as we have just explained,
$G_{0,\widetilde{S}}^{n}$
, which are effective as we have just explained,
![]() $G_{0,\widetilde{S}}^{n}$
descends to a uniquely determined semi-abelian scheme
$G_{0,\widetilde{S}}^{n}$
descends to a uniquely determined semi-abelian scheme
![]() $G$
over
$G$
over
![]() $S$
, whose generic fiber
$S$
, whose generic fiber
![]() $G_{\unicode[STIX]{x1D702}}$
is an abelian scheme because
$G_{\unicode[STIX]{x1D702}}$
is an abelian scheme because
 $G_{\widetilde{\unicode[STIX]{x1D702}}}\cong G_{0,\widetilde{\unicode[STIX]{x1D702}}}^{n}$
is; and whose special fiber
$G_{\widetilde{\unicode[STIX]{x1D702}}}\cong G_{0,\widetilde{\unicode[STIX]{x1D702}}}^{n}$
is; and whose special fiber
![]() $G_{s}$
is canonically isomorphic to
$G_{s}$
is canonically isomorphic to
![]() $T_{s}$
because their descent data are both given by
$T_{s}$
because their descent data are both given by
![]() $\unicode[STIX]{x1D70C}$
. Such an assignment of
$\unicode[STIX]{x1D70C}$
. Such an assignment of
![]() $G$
to
$G$
to
![]() $T_{s}$
is functorial (and compatible with base field extensions) in the torus
$T_{s}$
is functorial (and compatible with base field extensions) in the torus
![]() $T_{s}$
because the construction of
$T_{s}$
because the construction of
![]() $G$
by descent depends only on the descent data for
$G$
by descent depends only on the descent data for
![]() $T_{s}$
and on the choice of
$T_{s}$
and on the choice of
![]() $G_{0}$
.◻
$G_{0}$
.◻
Thus, we have reduced the more naive Question 1.1 to the case of the one-dimensional split torus
![]() $\mathbb{G}_{\text{m}}$
(over any base field), which can then be answered by the classical theory of Tate curves (see, for example, the rather universal construction over
$\mathbb{G}_{\text{m}}$
(over any base field), which can then be answered by the classical theory of Tate curves (see, for example, the rather universal construction over
![]() $\mathbb{Z}[[q]]$
in [Reference Deligne, Rapoport, Deligne and Kuyk5, Ch. VII]). However, any
$\mathbb{Z}[[q]]$
in [Reference Deligne, Rapoport, Deligne and Kuyk5, Ch. VII]). However, any
![]() $G$
given by Proposition 3.2 (or any assignment that is functorial and compatible with base field extensions in
$G$
given by Proposition 3.2 (or any assignment that is functorial and compatible with base field extensions in
![]() $T_{s}$
) must satisfy
$T_{s}$
) must satisfy
 $G_{\widetilde{\unicode[STIX]{x1D702}}}\cong G_{0,\widetilde{\unicode[STIX]{x1D702}}}^{n}$
over some extension
$G_{\widetilde{\unicode[STIX]{x1D702}}}\cong G_{0,\widetilde{\unicode[STIX]{x1D702}}}^{n}$
over some extension
![]() $\widetilde{\unicode[STIX]{x1D702}}$
of
$\widetilde{\unicode[STIX]{x1D702}}$
of
![]() $\unicode[STIX]{x1D702}$
, which cannot be absolutely simple when
$\unicode[STIX]{x1D702}$
, which cannot be absolutely simple when
![]() $n>1$
, and hence cannot be used to answer Question 1.2. We need a theory more general than that of Tate curves, which we shall review in the following section.
$n>1$
, and hence cannot be used to answer Question 1.2. We need a theory more general than that of Tate curves, which we shall review in the following section.
4 Theory of degeneration
Let
![]() $R$
be a complete discrete valuation ring with residue field
$R$
be a complete discrete valuation ring with residue field
![]() $k$
and fraction field
$k$
and fraction field
![]() $K$
. Let
$K$
. Let
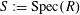 $S:=\operatorname{Spec}(R)$
,
$S:=\operatorname{Spec}(R)$
,
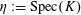 $\unicode[STIX]{x1D702}:=\operatorname{Spec}(K)$
, and
$\unicode[STIX]{x1D702}:=\operatorname{Spec}(K)$
, and
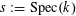 $s:=\operatorname{Spec}(k)$
. We shall denote the pullbacks to
$s:=\operatorname{Spec}(k)$
. We shall denote the pullbacks to
![]() $\unicode[STIX]{x1D702}$
or
$\unicode[STIX]{x1D702}$
or
![]() $s$
by subscripts
$s$
by subscripts
![]() $\unicode[STIX]{x1D702}$
or
$\unicode[STIX]{x1D702}$
or
![]() $s$
, respectively.
$s$
, respectively.
Definition 4.1 (Cf. [Reference Lan14, Definition 4.4.2]).
With the setting as above, the category
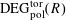 $\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
has objects consisting of pairs
$\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
has objects consisting of pairs
![]() $(G,\unicode[STIX]{x1D706})$
over
$(G,\unicode[STIX]{x1D706})$
over
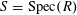 $S=\operatorname{Spec}(R)$
, where the following hold.
$S=\operatorname{Spec}(R)$
, where the following hold.
(1) The first entry
 $G$
is a semi-abelian scheme over
$G$
is a semi-abelian scheme over
 $S$
.
$S$
.(2) The pullback
 $G_{\unicode[STIX]{x1D702}}$
is an abelian scheme over
$G_{\unicode[STIX]{x1D702}}$
is an abelian scheme over
 $\unicode[STIX]{x1D702}$
, in which case there is a unique semi-abelian scheme
$\unicode[STIX]{x1D702}$
, in which case there is a unique semi-abelian scheme
 $G^{\vee }$
(up to unique isomorphism) over
$G^{\vee }$
(up to unique isomorphism) over
 $S$
, called the dual semi-abelian scheme of
$S$
, called the dual semi-abelian scheme of
 $G$
, such that
$G$
, such that
 $G_{\unicode[STIX]{x1D702}}^{\vee }$
is the dual abelian scheme of
$G_{\unicode[STIX]{x1D702}}^{\vee }$
is the dual abelian scheme of
 $G_{\unicode[STIX]{x1D702}}$
(see [Reference Lan14, §3.4.3]).
$G_{\unicode[STIX]{x1D702}}$
(see [Reference Lan14, §3.4.3]).(3) The pullback
 $G_{s}$
is a torus over
$G_{s}$
is a torus over
 $s$
(in which case
$s$
(in which case
 $G_{s}^{\vee }$
also is).
$G_{s}^{\vee }$
also is).(4) The second entry
 $\unicode[STIX]{x1D706}:G\rightarrow G^{\vee }$
is a group homomorphism that induces by restriction a polarization
$\unicode[STIX]{x1D706}:G\rightarrow G^{\vee }$
is a group homomorphism that induces by restriction a polarization
 $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D702}}$
of
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D702}}$
of
 $G_{\unicode[STIX]{x1D702}}$
.
$G_{\unicode[STIX]{x1D702}}$
.
Remark 4.2. The definition of pairs
![]() $(G,\unicode[STIX]{x1D706})$
as in Definition 4.1 extends verbatim to the case where
$(G,\unicode[STIX]{x1D706})$
as in Definition 4.1 extends verbatim to the case where
![]() $S$
is a noetherian normal local scheme, but we stated the definition this way only because the theory of degeneration below requires
$S$
is a noetherian normal local scheme, but we stated the definition this way only because the theory of degeneration below requires
![]() $R$
to be complete, and we only need the special case over Dedekind domains.
$R$
to be complete, and we only need the special case over Dedekind domains.
Remark 4.3. By [Reference Raynaud19, XI, 1.13, and IX, 1.4] (see also [Reference Lan14, Remarks 3.3.3.9 and 4.4.3, and Proposition 3.3.1.5]), any semi-abelian scheme
![]() $G$
over a noetherian normal domain
$G$
over a noetherian normal domain
![]() $R$
that is generically an abelian variety is automatically equipped with a homomorphism
$R$
that is generically an abelian variety is automatically equipped with a homomorphism
 $\unicode[STIX]{x1D706}:G\rightarrow G^{\vee }$
that is generically a polarization (of an abelian variety). In particular, any semi-abelian scheme
$\unicode[STIX]{x1D706}:G\rightarrow G^{\vee }$
that is generically a polarization (of an abelian variety). In particular, any semi-abelian scheme
![]() $G$
over
$G$
over
![]() $S$
satisfying the first two conditions in Definition 4.1 is automatically equipped with some homomorphism
$S$
satisfying the first two conditions in Definition 4.1 is automatically equipped with some homomorphism
 $\unicode[STIX]{x1D706}:G\rightarrow G^{\vee }$
satisfying the last condition in Definition 4.1.
$\unicode[STIX]{x1D706}:G\rightarrow G^{\vee }$
satisfying the last condition in Definition 4.1.
By the theory of degeneration data (see [Reference Mumford18]; see also [Reference Faltings and Chai7, Chs II and III] and [Reference Lan14, Ch. 4; see, in particular, Corollary 4.5.4.31], with all abelian parts in the degenerations suppressed; or see, for example, [Reference Lütkebohmert16, §2.7], for the corresponding rigid analytic theory, which is in some sense simpler), there is an equivalence of categories
 $$\begin{eqnarray}\operatorname{M}_{\text{pol}}^{\text{tor}}(R):\;\operatorname{DD}_{\text{pol}}^{\text{tor}}(R)\rightarrow \operatorname{DEG}_{\text{pol}}^{\text{tor}}(R):(\text{}\underline{X},\text{}\underline{Y},\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F})\mapsto (G,\unicode[STIX]{x1D706})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{M}_{\text{pol}}^{\text{tor}}(R):\;\operatorname{DD}_{\text{pol}}^{\text{tor}}(R)\rightarrow \operatorname{DEG}_{\text{pol}}^{\text{tor}}(R):(\text{}\underline{X},\text{}\underline{Y},\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F})\mapsto (G,\unicode[STIX]{x1D706})\end{eqnarray}$$
realizing
![]() $(G,\unicode[STIX]{x1D706})$
(up to isomorphism) as the image of an object in
$(G,\unicode[STIX]{x1D706})$
(up to isomorphism) as the image of an object in
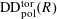 $\operatorname{DD}_{\text{pol}}^{\text{tor}}(R)$
given by the following data.
$\operatorname{DD}_{\text{pol}}^{\text{tor}}(R)$
given by the following data.
(1) Two étale sheaves
 $\text{}\underline{X}$
and
$\text{}\underline{X}$
and
 $\text{}\underline{Y}$
of free abelian groups of finite ranks over
$\text{}\underline{Y}$
of free abelian groups of finite ranks over
 $S$
, together with an embedding
$S$
, together with an embedding
 $\unicode[STIX]{x1D719}:\text{}\underline{Y}\rightarrow \text{}\underline{X}$
with finite cokernel (here
$\unicode[STIX]{x1D719}:\text{}\underline{Y}\rightarrow \text{}\underline{X}$
with finite cokernel (here
 $\unicode[STIX]{x1D719}:\text{}\underline{Y}\rightarrow \text{}\underline{X}$
corresponds to the isogeny of tori
$\unicode[STIX]{x1D719}:\text{}\underline{Y}\rightarrow \text{}\underline{X}$
corresponds to the isogeny of tori
 $T\rightarrow T^{\vee }$
uniquely lifting
$T\rightarrow T^{\vee }$
uniquely lifting
 $G_{s}\rightarrow G_{s}^{\vee }$
, by Lemma 3.1. It should be noted that the notation for objects related to the degeneration of
$G_{s}\rightarrow G_{s}^{\vee }$
, by Lemma 3.1. It should be noted that the notation for objects related to the degeneration of
 $G_{\unicode[STIX]{x1D702}}^{\vee }$
, such as
$G_{\unicode[STIX]{x1D702}}^{\vee }$
, such as
 $T^{\vee }$
, is only symbolic in nature).
$T^{\vee }$
, is only symbolic in nature).(2) A bimultiplicative homomorphism
 $\unicode[STIX]{x1D70F}:\text{}\underline{Y}_{\unicode[STIX]{x1D702}}\times \text{}\underline{X}_{\unicode[STIX]{x1D702}}\rightarrow \mathbb{G}_{\text{m},\unicode[STIX]{x1D702}}$
of étale sheaves over
$\unicode[STIX]{x1D70F}:\text{}\underline{Y}_{\unicode[STIX]{x1D702}}\times \text{}\underline{X}_{\unicode[STIX]{x1D702}}\rightarrow \mathbb{G}_{\text{m},\unicode[STIX]{x1D702}}$
of étale sheaves over
 $\unicode[STIX]{x1D702}$
with symmetric pullback under
$\unicode[STIX]{x1D702}$
with symmetric pullback under
 $\operatorname{Id}_{\text{}\underline{Y}}\times \text{}\underline{\unicode[STIX]{x1D719}}:\text{}\underline{Y}\times \text{}\underline{Y}\rightarrow \text{}\underline{Y}\times \text{}\underline{X}$
, satisfying the following positivity condition for some (and hence every) finite extension
$\operatorname{Id}_{\text{}\underline{Y}}\times \text{}\underline{\unicode[STIX]{x1D719}}:\text{}\underline{Y}\times \text{}\underline{Y}\rightarrow \text{}\underline{Y}\times \text{}\underline{X}$
, satisfying the following positivity condition for some (and hence every) finite extension
 $\widetilde{K}$
of
$\widetilde{K}$
of
 $K$
as in §3 over which both
$K$
as in §3 over which both
 $\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and
$\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and
 $\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
, where
$\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
, where
 $\widetilde{\unicode[STIX]{x1D702}}:=\operatorname{Spec}(\widetilde{K})$
, are constant:
$\widetilde{\unicode[STIX]{x1D702}}:=\operatorname{Spec}(\widetilde{K})$
, are constant:
 $\widetilde{\unicode[STIX]{x1D710}}(\unicode[STIX]{x1D70F}(y,\unicode[STIX]{x1D719}(y)))>0$
for every non-zero section
$\widetilde{\unicode[STIX]{x1D710}}(\unicode[STIX]{x1D70F}(y,\unicode[STIX]{x1D719}(y)))>0$
for every non-zero section
 $y$
of
$y$
of
 $\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
, where
$\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
, where
 $\widetilde{\unicode[STIX]{x1D710}}:\widetilde{K}^{\times }\rightarrow \mathbb{Z}$
is any non-trivial discrete valuation of
$\widetilde{\unicode[STIX]{x1D710}}:\widetilde{K}^{\times }\rightarrow \mathbb{Z}$
is any non-trivial discrete valuation of
 $\widetilde{K}$
.
$\widetilde{K}$
.
We say that
 $(\text{}\underline{X},\text{}\underline{Y},\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F})$
is the degeneration data of
$(\text{}\underline{X},\text{}\underline{Y},\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F})$
is the degeneration data of
![]() $(G,\unicode[STIX]{x1D706})$
.
$(G,\unicode[STIX]{x1D706})$
.
Remark 4.4. The bimultiplicative homomorphism
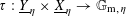 $\unicode[STIX]{x1D70F}:\text{}\underline{Y}_{\unicode[STIX]{x1D702}}\times \text{}\underline{X}_{\unicode[STIX]{x1D702}}\rightarrow \mathbb{G}_{\text{m},\unicode[STIX]{x1D702}}$
induces (by the definition of
$\unicode[STIX]{x1D70F}:\text{}\underline{Y}_{\unicode[STIX]{x1D702}}\times \text{}\underline{X}_{\unicode[STIX]{x1D702}}\rightarrow \mathbb{G}_{\text{m},\unicode[STIX]{x1D702}}$
induces (by the definition of
![]() $\text{}\underline{X}$
as the character group of
$\text{}\underline{X}$
as the character group of
![]() $T$
) a homomorphism
$T$
) a homomorphism
 $$\begin{eqnarray}\unicode[STIX]{x1D704}:\text{}\underline{Y}_{\unicode[STIX]{x1D702}}\rightarrow T_{\unicode[STIX]{x1D702}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D704}:\text{}\underline{Y}_{\unicode[STIX]{x1D702}}\rightarrow T_{\unicode[STIX]{x1D702}},\end{eqnarray}$$
which is a generalization of the familiar Tate periods in the case of relative dimension one (i.e. of Tate curves). Nevertheless, we will not need
![]() $\unicode[STIX]{x1D704}$
in what follows.
$\unicode[STIX]{x1D704}$
in what follows.
5 Conditions for degenerations
Let
![]() $R$
,
$R$
,
![]() $k$
,
$k$
,
![]() $K$
,
$K$
,
![]() $S$
,
$S$
,
![]() $s$
, and
$s$
, and
![]() $\unicode[STIX]{x1D702}$
be as in the beginning of §4.
$\unicode[STIX]{x1D702}$
be as in the beginning of §4.
Suppose that we have tori
![]() $T_{s}$
and
$T_{s}$
and
![]() $T_{s}^{\vee }$
over
$T_{s}^{\vee }$
over
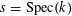 $s=\operatorname{Spec}(k)$
with character groups
$s=\operatorname{Spec}(k)$
with character groups
![]() $\text{}\underline{X}_{s}$
and
$\text{}\underline{X}_{s}$
and
![]() $\text{}\underline{Y}_{s}$
that are étale sheaves of free abelian groups of finite ranks, together with an embedding
$\text{}\underline{Y}_{s}$
that are étale sheaves of free abelian groups of finite ranks, together with an embedding
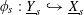 $\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
with finite cokernel inducing an isogeny
$\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
with finite cokernel inducing an isogeny
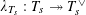 $\unicode[STIX]{x1D706}_{T_{s}}:T_{s}{\twoheadrightarrow}T_{s}^{\vee }$
. (Certainly, we allow
$\unicode[STIX]{x1D706}_{T_{s}}:T_{s}{\twoheadrightarrow}T_{s}^{\vee }$
. (Certainly, we allow
![]() $\unicode[STIX]{x1D719}_{s}$
and hence
$\unicode[STIX]{x1D719}_{s}$
and hence
![]() $\unicode[STIX]{x1D706}_{T_{s}}$
to be isomorphisms.) In this section, we shall find necessary and sufficient conditions for the existence of an object
$\unicode[STIX]{x1D706}_{T_{s}}$
to be isomorphisms.) In this section, we shall find necessary and sufficient conditions for the existence of an object
![]() $(G,\unicode[STIX]{x1D706})$
in
$(G,\unicode[STIX]{x1D706})$
in
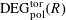 $\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
such that
$\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
such that
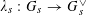 $\unicode[STIX]{x1D706}_{s}:G_{s}\rightarrow G_{s}^{\vee }$
can be identified with
$\unicode[STIX]{x1D706}_{s}:G_{s}\rightarrow G_{s}^{\vee }$
can be identified with
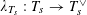 $\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some isomorphisms
$\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some isomorphisms
![]() $G_{s}\cong T_{s}$
and
$G_{s}\cong T_{s}$
and
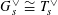 $G_{s}^{\vee }\cong T_{s}^{\vee }$
over
$G_{s}^{\vee }\cong T_{s}^{\vee }$
over
![]() $s$
), and such that
$s$
), and such that
![]() $G_{\unicode[STIX]{x1D702}}$
and hence
$G_{\unicode[STIX]{x1D702}}$
and hence
![]() $G_{\unicode[STIX]{x1D702}}^{\vee }$
are absolutely simple abelian varieties.
$G_{\unicode[STIX]{x1D702}}^{\vee }$
are absolutely simple abelian varieties.
By Lemma 3.1, the embedding
 $\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
lifts to an embedding
$\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
lifts to an embedding
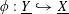 $\unicode[STIX]{x1D719}:\text{}\underline{Y}{\hookrightarrow}\text{}\underline{X}$
with finite cokernel over
$\unicode[STIX]{x1D719}:\text{}\underline{Y}{\hookrightarrow}\text{}\underline{X}$
with finite cokernel over
![]() $S$
of étale sheaves of free abelian groups of finite ranks, inducing an isogeny
$S$
of étale sheaves of free abelian groups of finite ranks, inducing an isogeny
 $\unicode[STIX]{x1D706}_{T}:T{\twoheadrightarrow}T^{\vee }$
(between isotrivial tori) lifting
$\unicode[STIX]{x1D706}_{T}:T{\twoheadrightarrow}T^{\vee }$
(between isotrivial tori) lifting
![]() $\unicode[STIX]{x1D706}_{T_{s}}$
. Let
$\unicode[STIX]{x1D706}_{T_{s}}$
. Let
![]() $\widetilde{S}$
, etc, be as in §3 such that both
$\widetilde{S}$
, etc, be as in §3 such that both
![]() $\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and
$\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and
![]() $\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
are constant of some common finite rank
$\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
are constant of some common finite rank
![]() $n$
, so that there are isomorphisms
$n$
, so that there are isomorphisms
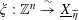 $\unicode[STIX]{x1D709}:\mathbb{Z}^{n}\stackrel{{\sim}}{\rightarrow }\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and
$\unicode[STIX]{x1D709}:\mathbb{Z}^{n}\stackrel{{\sim}}{\rightarrow }\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and
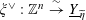 $\unicode[STIX]{x1D709}^{\vee }:\mathbb{Z}^{n}\stackrel{{\sim}}{\rightarrow }\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
and representations
$\unicode[STIX]{x1D709}^{\vee }:\mathbb{Z}^{n}\stackrel{{\sim}}{\rightarrow }\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
and representations
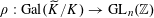 $\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
and
$\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
and
 $\unicode[STIX]{x1D70C}^{\vee }:\operatorname{Gal}(\widetilde{K}/K)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
defining the descent data for the étale sheaves
$\unicode[STIX]{x1D70C}^{\vee }:\operatorname{Gal}(\widetilde{K}/K)\rightarrow \operatorname{GL}_{n}(\mathbb{Z})$
defining the descent data for the étale sheaves
![]() $\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and
$\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and
![]() $\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
. Consider
$\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
. Consider
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:=\unicode[STIX]{x1D709}^{-1}\;\unicode[STIX]{x1D719}_{\widetilde{\unicode[STIX]{x1D702}}}\;\unicode[STIX]{x1D709}^{\vee }:\mathbb{Z}^{n}\rightarrow \mathbb{Z}^{n},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:=\unicode[STIX]{x1D709}^{-1}\;\unicode[STIX]{x1D719}_{\widetilde{\unicode[STIX]{x1D702}}}\;\unicode[STIX]{x1D709}^{\vee }:\mathbb{Z}^{n}\rightarrow \mathbb{Z}^{n},\end{eqnarray}$$
which defines an element of
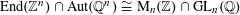 $\operatorname{End}(\mathbb{Z}^{n})\cap \operatorname{Aut}(\mathbb{Q}^{n})\cong \operatorname{M}_{n}(\mathbb{Z})\cap \operatorname{GL}_{n}(\mathbb{Q})$
.
$\operatorname{End}(\mathbb{Z}^{n})\cap \operatorname{Aut}(\mathbb{Q}^{n})\cong \operatorname{M}_{n}(\mathbb{Z})\cap \operatorname{GL}_{n}(\mathbb{Q})$
.
Lemma 5.2. We have
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(\unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D6FE})z)=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(\unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D6FE})z)=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z))\end{eqnarray}$$
for all
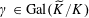 $\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
and
$\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
and
![]() $z\in \mathbb{Z}^{n}$
.
$z\in \mathbb{Z}^{n}$
.
Proof. This is because
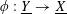 $\unicode[STIX]{x1D719}:\text{}\underline{Y}\rightarrow \text{}\underline{X}$
is a morphism defined over
$\unicode[STIX]{x1D719}:\text{}\underline{Y}\rightarrow \text{}\underline{X}$
is a morphism defined over
![]() $S$
.◻
$S$
.◻
Proposition 5.3. With the setting as above, with the fixed choices of some
![]() $\unicode[STIX]{x1D709}$
,
$\unicode[STIX]{x1D709}$
,
![]() $\unicode[STIX]{x1D709}^{\vee }$
,
$\unicode[STIX]{x1D709}^{\vee }$
,
![]() $\unicode[STIX]{x1D70C}$
, and
$\unicode[STIX]{x1D70C}$
, and
![]() $\unicode[STIX]{x1D70C}^{\vee }$
, the datum of an object
$\unicode[STIX]{x1D70C}^{\vee }$
, the datum of an object
![]() $(G,\unicode[STIX]{x1D706})$
of
$(G,\unicode[STIX]{x1D706})$
of
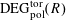 $\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
(as in Definition 4.1) such that
$\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
(as in Definition 4.1) such that
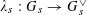 $\unicode[STIX]{x1D706}_{s}:G_{s}\rightarrow G_{s}^{\vee }$
can be identified with
$\unicode[STIX]{x1D706}_{s}:G_{s}\rightarrow G_{s}^{\vee }$
can be identified with
 $\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some isomorphisms
$\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some isomorphisms
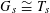 $G_{s}\cong T_{s}$
and
$G_{s}\cong T_{s}$
and
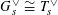 $G_{s}^{\vee }\cong T_{s}^{\vee }$
over
$G_{s}^{\vee }\cong T_{s}^{\vee }$
over
![]() $s$
) is equivalent to the datum of a bimultiplicative pairing
$s$
) is equivalent to the datum of a bimultiplicative pairing
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
satisfying the following conditions.
(1) (Galois equivariance)
 $\langle \unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\unicode[STIX]{x1D6FE}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
for all
$\langle \unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\unicode[STIX]{x1D6FE}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
for all
 $z,w\in \mathbb{Z}^{n}$
and
$z,w\in \mathbb{Z}^{n}$
and
 $\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
(note that the action of
$\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
(note that the action of
 $\operatorname{Gal}(\widetilde{K}/K)$
on
$\operatorname{Gal}(\widetilde{K}/K)$
on
 $\widetilde{K}^{\times }$
here is the naive one, because
$\widetilde{K}^{\times }$
here is the naive one, because
 $\widetilde{K}^{\times }$
is just the group of points of
$\widetilde{K}^{\times }$
is just the group of points of
 $\mathbb{G}_{\text{m}}$
over
$\mathbb{G}_{\text{m}}$
over
 $\widetilde{\unicode[STIX]{x1D702}}=\operatorname{Spec}(\widetilde{K})$
, and
$\widetilde{\unicode[STIX]{x1D702}}=\operatorname{Spec}(\widetilde{K})$
, and
 $\mathbb{G}_{\text{m}}$
is already defined over
$\mathbb{G}_{\text{m}}$
is already defined over
 $\unicode[STIX]{x1D702}=\operatorname{Spec}(K)$
or rather
$\unicode[STIX]{x1D702}=\operatorname{Spec}(K)$
or rather
 $\operatorname{Spec}(\mathbb{Z})$
).
$\operatorname{Spec}(\mathbb{Z})$
).(2) (Symmetry)
 $\langle z,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(w)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle w,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
for all
$\langle z,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(w)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle w,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
for all
 $z,w\in \mathbb{Z}^{n}$
.
$z,w\in \mathbb{Z}^{n}$
.(3) (Positivity)
 $\widetilde{\unicode[STIX]{x1D710}}(\langle z,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }})>0$
for every non-zero
$\widetilde{\unicode[STIX]{x1D710}}(\langle z,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }})>0$
for every non-zero
 $z\in \mathbb{Z}^{n}$
, where
$z\in \mathbb{Z}^{n}$
, where
 $\widetilde{\unicode[STIX]{x1D710}}:\widetilde{K}^{\times }\rightarrow \mathbb{Z}$
is any non-trivial discrete valuation of
$\widetilde{\unicode[STIX]{x1D710}}:\widetilde{K}^{\times }\rightarrow \mathbb{Z}$
is any non-trivial discrete valuation of
 $\widetilde{K}$
.
$\widetilde{K}$
.
Proof. This follows from the theory reviewed in §4, by base change to
![]() $\widetilde{\unicode[STIX]{x1D702}}$
, by pulling back under
$\widetilde{\unicode[STIX]{x1D702}}$
, by pulling back under
![]() $\unicode[STIX]{x1D709}^{\vee }\times \unicode[STIX]{x1D709}$
, and by descent (as in the proof of Proposition 3.2).◻
$\unicode[STIX]{x1D709}^{\vee }\times \unicode[STIX]{x1D709}$
, and by descent (as in the proof of Proposition 3.2).◻
Proposition 5.5. In the setting of Proposition 5.3, if the pairing
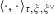 $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
corresponding to
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
corresponding to
![]() $(G,\unicode[STIX]{x1D706})$
satisfies the additional condition that
$(G,\unicode[STIX]{x1D706})$
satisfies the additional condition that
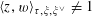 $$\begin{eqnarray}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1\end{eqnarray}$$
$$\begin{eqnarray}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1\end{eqnarray}$$
for all non-zero
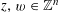 $z,w\in \mathbb{Z}^{n}$
, then
$z,w\in \mathbb{Z}^{n}$
, then
![]() $G_{\unicode[STIX]{x1D702}}$
and hence
$G_{\unicode[STIX]{x1D702}}$
and hence
![]() $G_{\unicode[STIX]{x1D702}}^{\vee }$
must be absolutely simple.
$G_{\unicode[STIX]{x1D702}}^{\vee }$
must be absolutely simple.
Proof. Suppose
![]() $G_{\unicode[STIX]{x1D702}}$
is not absolutely simple. Then there exists a finite extension
$G_{\unicode[STIX]{x1D702}}$
is not absolutely simple. Then there exists a finite extension
![]() $K^{\prime }$
of
$K^{\prime }$
of
![]() $\widetilde{K}$
over which the base change of
$\widetilde{K}$
over which the base change of
![]() $G_{\unicode[STIX]{x1D702}}$
is isogenous to a non-trivial product of two abelian varieties of smaller dimension. By the theory of Néron models (see, in particular, [Reference Bosch, Lütkebohmert and Raybaud3, Ch. 7, §7.4, Theorem 1]), up to replacing
$G_{\unicode[STIX]{x1D702}}$
is isogenous to a non-trivial product of two abelian varieties of smaller dimension. By the theory of Néron models (see, in particular, [Reference Bosch, Lütkebohmert and Raybaud3, Ch. 7, §7.4, Theorem 1]), up to replacing
![]() $K^{\prime }$
with a finite extension, we may assume that these two abelian varieties extend to two semi-abelian schemes
$K^{\prime }$
with a finite extension, we may assume that these two abelian varieties extend to two semi-abelian schemes
![]() $G_{1}$
and
$G_{1}$
and
![]() $G_{2}$
, respectively, over the integral closure
$G_{2}$
, respectively, over the integral closure
![]() $R^{\prime }$
of
$R^{\prime }$
of
![]() $R$
in
$R$
in
![]() $K^{\prime }$
. Since the theory of degeneration in §4 is an equivalence of categories, there exist some non-zero
$K^{\prime }$
. Since the theory of degeneration in §4 is an equivalence of categories, there exist some non-zero
 $z,w\in \mathbb{Z}^{n}$
, which are the images of some elements of the character groups of the torus parts of
$z,w\in \mathbb{Z}^{n}$
, which are the images of some elements of the character groups of the torus parts of
![]() $G_{1}^{\vee }$
and
$G_{1}^{\vee }$
and
![]() $G_{2}$
, such that
$G_{2}$
, such that
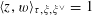 $\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=1$
(in
$\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=1$
(in
![]() $K^{\prime }$
, and hence also in
$K^{\prime }$
, and hence also in
![]() $\widetilde{K}$
). This contradicts the condition (5.6) in this proposition, as desired.◻
$\widetilde{K}$
). This contradicts the condition (5.6) in this proposition, as desired.◻
In the remainder of this section, let us show that the conditions in Propositions 5.3 and 5.5 can indeed be achieved by some bimultiplicative pairing
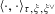 $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
.
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
.
Lemma 5.7. There exists
![]() $\unicode[STIX]{x1D703}\in \widetilde{R}^{\times }$
such that
$\unicode[STIX]{x1D703}\in \widetilde{R}^{\times }$
such that
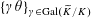 $\{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D703}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
form a free
$\{\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D703}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
form a free
![]() $R$
-basis of
$R$
-basis of
![]() $\widetilde{R}$
, and such that the reductions
$\widetilde{R}$
, and such that the reductions
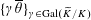 $\{\unicode[STIX]{x1D6FE}\overline{\unicode[STIX]{x1D703}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
in
$\{\unicode[STIX]{x1D6FE}\overline{\unicode[STIX]{x1D703}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
in
![]() $\widetilde{k}$
form a
$\widetilde{k}$
form a
![]() $k$
-basis of
$k$
-basis of
![]() $\widetilde{k}$
.
$\widetilde{k}$
.
Proof. Since
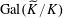 $\operatorname{Gal}(\widetilde{K}/K)$
is a finite group, the group algebra
$\operatorname{Gal}(\widetilde{K}/K)$
is a finite group, the group algebra
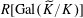 $R[\operatorname{Gal}(\widetilde{K}/K)]$
over
$R[\operatorname{Gal}(\widetilde{K}/K)]$
over
![]() $R$
is an
$R$
is an
![]() $R$
-order (see [Reference Lan14, Definition 1.1.1.3]) in the finite-dimensional group algebra
$R$
-order (see [Reference Lan14, Definition 1.1.1.3]) in the finite-dimensional group algebra
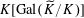 $K[\operatorname{Gal}(\widetilde{K}/K)]$
over
$K[\operatorname{Gal}(\widetilde{K}/K)]$
over
![]() $K$
. Since
$K$
. Since
![]() $\widetilde{R}$
is finite étale over
$\widetilde{R}$
is finite étale over
![]() $R$
, we have
$R$
, we have
 $\operatorname{Gal}(\widetilde{K}/K)\cong \operatorname{Gal}(\widetilde{k}/k)$
as groups, and
$\operatorname{Gal}(\widetilde{K}/K)\cong \operatorname{Gal}(\widetilde{k}/k)$
as groups, and
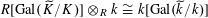 $R[\operatorname{Gal}(\widetilde{K}/K)]\otimes _{R}k\cong k[\operatorname{Gal}(\widetilde{k}/k)]$
as group algebras over
$R[\operatorname{Gal}(\widetilde{K}/K)]\otimes _{R}k\cong k[\operatorname{Gal}(\widetilde{k}/k)]$
as group algebras over
![]() $k$
. By applying the normal basis theorem (see, for example, [Reference Lang15, Ch. VI, §13]) to the finite Galois field extension
$k$
. By applying the normal basis theorem (see, for example, [Reference Lang15, Ch. VI, §13]) to the finite Galois field extension
![]() $\widetilde{k}/k$
, we have
$\widetilde{k}/k$
, we have
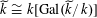 $\widetilde{k}\cong k[\operatorname{Gal}(\widetilde{k}/k)]$
as left
$\widetilde{k}\cong k[\operatorname{Gal}(\widetilde{k}/k)]$
as left
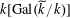 $k[\operatorname{Gal}(\widetilde{k}/k)]$
-modules. Therefore, since
$k[\operatorname{Gal}(\widetilde{k}/k)]$
-modules. Therefore, since
![]() $R$
is local with residue field
$R$
is local with residue field
![]() $k$
, by [Reference Lan14, Lemma 1.1.3.1] (which is a consequence of the usual Nakayama’s lemma for finitely generated
$k$
, by [Reference Lan14, Lemma 1.1.3.1] (which is a consequence of the usual Nakayama’s lemma for finitely generated
![]() $R$
-modules), we have
$R$
-modules), we have
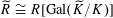 $\widetilde{R}\cong R[\operatorname{Gal}(\widetilde{K}/K)]$
as left
$\widetilde{R}\cong R[\operatorname{Gal}(\widetilde{K}/K)]$
as left
 $R[\operatorname{Gal}(\widetilde{K}/K)]$
-modules, and the lemma follows.◻
$R[\operatorname{Gal}(\widetilde{K}/K)]$
-modules, and the lemma follows.◻
Lemma 5.8. There exists
 $u_{0}\in \widetilde{R}^{\times }$
such that the Galois conjugates
$u_{0}\in \widetilde{R}^{\times }$
such that the Galois conjugates
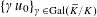 $\{\unicode[STIX]{x1D6FE}u_{0}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
are multiplicatively independent in the sense that, if
$\{\unicode[STIX]{x1D6FE}u_{0}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
are multiplicatively independent in the sense that, if
 $$\begin{eqnarray}\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{0})^{c_{\unicode[STIX]{x1D6FE}}}=1\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{0})^{c_{\unicode[STIX]{x1D6FE}}}=1\end{eqnarray}$$
in
![]() $\widetilde{R}^{\times }$
for some integers
$\widetilde{R}^{\times }$
for some integers
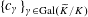 $\{c_{\unicode[STIX]{x1D6FE}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
, then these integers are all zero.
$\{c_{\unicode[STIX]{x1D6FE}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
, then these integers are all zero.
Proof. Let
![]() $I$
and
$I$
and
![]() $\widetilde{I}$
denote the maximal ideals of
$\widetilde{I}$
denote the maximal ideals of
![]() $R$
and
$R$
and
![]() $\widetilde{R}$
, respectively, which satisfy
$\widetilde{R}$
, respectively, which satisfy
 $\widetilde{I}=I\cdot \widetilde{R}$
because
$\widetilde{I}=I\cdot \widetilde{R}$
because
![]() $\widetilde{R}$
is finite étale over
$\widetilde{R}$
is finite étale over
![]() $R$
. If
$R$
. If
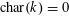 $\operatorname{char}(k)=0$
, we set
$\operatorname{char}(k)=0$
, we set
![]() $\unicode[STIX]{x1D6FF}=0$
. Otherwise, we have
$\unicode[STIX]{x1D6FF}=0$
. Otherwise, we have
 $\operatorname{char}(k)=p$
for some rational prime number
$\operatorname{char}(k)=p$
for some rational prime number
![]() $p>0$
, and we fix the choice of any integer
$p>0$
, and we fix the choice of any integer
![]() $\unicode[STIX]{x1D6FF}\geqslant 0$
such that the multiplicative subgroup
$\unicode[STIX]{x1D6FF}\geqslant 0$
such that the multiplicative subgroup
 $1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}}$
of
$1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}}$
of
![]() $\widetilde{R}^{\times }$
does not contain any non-trivial
$\widetilde{R}^{\times }$
does not contain any non-trivial
![]() $p$
th roots of unity. (Such an integer
$p$
th roots of unity. (Such an integer
![]() $\unicode[STIX]{x1D6FF}$
always exists, because there are only finitely many
$\unicode[STIX]{x1D6FF}$
always exists, because there are only finitely many
![]() $p$
th root of unity in
$p$
th root of unity in
![]() $\widetilde{K}$
or any field, and because
$\widetilde{K}$
or any field, and because
![]() $\widetilde{R}$
is
$\widetilde{R}$
is
![]() $\widetilde{I}$
-adically separated.)
$\widetilde{I}$
-adically separated.)
Let
![]() $\unicode[STIX]{x1D703}\in \widetilde{R}^{\times }$
be as in Lemma 5.7, let
$\unicode[STIX]{x1D703}\in \widetilde{R}^{\times }$
be as in Lemma 5.7, let
![]() $\unicode[STIX]{x1D71B}$
be any uniformizer of
$\unicode[STIX]{x1D71B}$
be any uniformizer of
![]() $R$
(which is then also a uniformizer of
$R$
(which is then also a uniformizer of
![]() $\widetilde{R}$
), let
$\widetilde{R}$
), let
![]() $\unicode[STIX]{x1D6FF}$
be as in the previous paragraph, and let
$\unicode[STIX]{x1D6FF}$
be as in the previous paragraph, and let
 $$\begin{eqnarray}u_{0}:=1+\unicode[STIX]{x1D703}\unicode[STIX]{x1D71B}^{1+\unicode[STIX]{x1D6FF}}\in 1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}}\subset \widetilde{R}^{\times }.\end{eqnarray}$$
$$\begin{eqnarray}u_{0}:=1+\unicode[STIX]{x1D703}\unicode[STIX]{x1D71B}^{1+\unicode[STIX]{x1D6FF}}\in 1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}}\subset \widetilde{R}^{\times }.\end{eqnarray}$$
We would like to show that
![]() $u_{0}$
satisfies the requirement of this lemma; namely, if
$u_{0}$
satisfies the requirement of this lemma; namely, if
 $$\begin{eqnarray}\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{0})^{c_{\unicode[STIX]{x1D6FE}}}=\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(1+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D703})\unicode[STIX]{x1D71B}^{1+\unicode[STIX]{x1D6FF}})^{c_{\unicode[STIX]{x1D6FE}}}=1\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{0})^{c_{\unicode[STIX]{x1D6FE}}}=\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(1+(\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D703})\unicode[STIX]{x1D71B}^{1+\unicode[STIX]{x1D6FF}})^{c_{\unicode[STIX]{x1D6FE}}}=1\end{eqnarray}$$
in
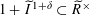 $1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}}\subset \widetilde{R}^{\times }$
for some integers
$1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}}\subset \widetilde{R}^{\times }$
for some integers
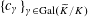 $\{c_{\unicode[STIX]{x1D6FE}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
, then these integers are all zero.
$\{c_{\unicode[STIX]{x1D6FE}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
, then these integers are all zero.
Suppose, to the contrary, that the relation (5.9) holds for some integers
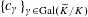 $\{c_{\unicode[STIX]{x1D6FE}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
that are not all zero. First, suppose
$\{c_{\unicode[STIX]{x1D6FE}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
that are not all zero. First, suppose
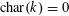 $\operatorname{char}(k)=0$
. Then
$\operatorname{char}(k)=0$
. Then
![]() $\mathbb{Q}\subset k$
, and the relation (5.9) implies that
$\mathbb{Q}\subset k$
, and the relation (5.9) implies that
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}c_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FE}\overline{\unicode[STIX]{x1D703}})=0\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}c_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FE}\overline{\unicode[STIX]{x1D703}})=0\end{eqnarray}$$
in
![]() $k$
, by considering the images of the terms in (5.9) in
$k$
, by considering the images of the terms in (5.9) in
 $(1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}})/(1+\widetilde{I}^{2+\unicode[STIX]{x1D6FF}})\cong k$
(where
$(1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}})/(1+\widetilde{I}^{2+\unicode[STIX]{x1D6FF}})\cong k$
(where
![]() $\unicode[STIX]{x1D6FF}=0$
). This contradicts the linear independence of
$\unicode[STIX]{x1D6FF}=0$
). This contradicts the linear independence of
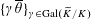 $\{\unicode[STIX]{x1D6FE}\overline{\unicode[STIX]{x1D703}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
over
$\{\unicode[STIX]{x1D6FE}\overline{\unicode[STIX]{x1D703}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
over
![]() $k$
. Otherwise, suppose
$k$
. Otherwise, suppose
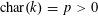 $\operatorname{char}(k)=p>0$
. Then there exists some power
$\operatorname{char}(k)=p>0$
. Then there exists some power
![]() $q$
of
$q$
of
![]() $p$
such that
$p$
such that
![]() $q|c_{\unicode[STIX]{x1D6FE}}$
for all
$q|c_{\unicode[STIX]{x1D6FE}}$
for all
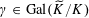 $\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
, but
$\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
, but
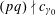 $(pq)\nmid c_{\unicode[STIX]{x1D6FE}_{0}}$
for at least one
$(pq)\nmid c_{\unicode[STIX]{x1D6FE}_{0}}$
for at least one
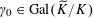 $\unicode[STIX]{x1D6FE}_{0}\in \operatorname{Gal}(\widetilde{K}/K)$
, so that the reductions
$\unicode[STIX]{x1D6FE}_{0}\in \operatorname{Gal}(\widetilde{K}/K)$
, so that the reductions
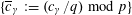 $\{\overline{c}_{\unicode[STIX]{x1D6FE}}:=(c_{\unicode[STIX]{x1D6FE}}/q)\hspace{0.2em}{\rm mod}\hspace{0.2em}p\}$
are not all zero in
$\{\overline{c}_{\unicode[STIX]{x1D6FE}}:=(c_{\unicode[STIX]{x1D6FE}}/q)\hspace{0.2em}{\rm mod}\hspace{0.2em}p\}$
are not all zero in
![]() $\mathbb{F}_{p}\subset k$
. By the choice of
$\mathbb{F}_{p}\subset k$
. By the choice of
![]() $\unicode[STIX]{x1D6FF}$
, the multiplicative subgroup
$\unicode[STIX]{x1D6FF}$
, the multiplicative subgroup
 $1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}}$
of
$1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}}$
of
![]() $\widetilde{R}^{\times }$
cannot contain any non-trivial
$\widetilde{R}^{\times }$
cannot contain any non-trivial
![]() $p$
th roots of unity, and consequently the relation (5.9) still holds with the
$p$
th roots of unity, and consequently the relation (5.9) still holds with the
![]() $c_{\unicode[STIX]{x1D6FE}}$
replaced with
$c_{\unicode[STIX]{x1D6FE}}$
replaced with
![]() $c_{\unicode[STIX]{x1D6FE}}/q$
. After such a replacement, again by considering the images of the terms in (5.9) in
$c_{\unicode[STIX]{x1D6FE}}/q$
. After such a replacement, again by considering the images of the terms in (5.9) in
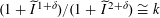 $(1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}})/(1+\widetilde{I}^{2+\unicode[STIX]{x1D6FF}})\cong k$
, we get that
$(1+\widetilde{I}^{1+\unicode[STIX]{x1D6FF}})/(1+\widetilde{I}^{2+\unicode[STIX]{x1D6FF}})\cong k$
, we get that
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}\overline{c}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FE}\overline{\unicode[STIX]{x1D703}})=0\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}\overline{c}_{\unicode[STIX]{x1D6FE}}(\unicode[STIX]{x1D6FE}\overline{\unicode[STIX]{x1D703}})=0\end{eqnarray}$$
in
![]() $k$
. This again contradicts the linear independence of
$k$
. This again contradicts the linear independence of
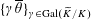 $\{\unicode[STIX]{x1D6FE}\overline{\unicode[STIX]{x1D703}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
over
$\{\unicode[STIX]{x1D6FE}\overline{\unicode[STIX]{x1D703}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
over
![]() $k$
. Thus, the integers
$k$
. Thus, the integers
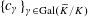 $\{c_{\unicode[STIX]{x1D6FE}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
must be all zero, and the lemma follows.◻
$\{c_{\unicode[STIX]{x1D6FE}}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
must be all zero, and the lemma follows.◻
Lemma 5.10. For any integer
![]() $N\geqslant 1$
, there exist elements
$N\geqslant 1$
, there exist elements
 $u_{1},u_{2},\ldots ,u_{N}$
in
$u_{1},u_{2},\ldots ,u_{N}$
in
![]() $\widetilde{R}^{\times }$
that are multiplicatively Galois independent in the sense that, if
$\widetilde{R}^{\times }$
that are multiplicatively Galois independent in the sense that, if
 $$\begin{eqnarray}\mathop{\prod }_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{i})^{c_{i,\unicode[STIX]{x1D6FE}}}=1\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{i})^{c_{i,\unicode[STIX]{x1D6FE}}}=1\end{eqnarray}$$
in
![]() $\widetilde{R}^{\times }$
for some integers
$\widetilde{R}^{\times }$
for some integers
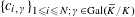 $\{c_{i,\unicode[STIX]{x1D6FE}}\}_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
, then these integers are all zero.
$\{c_{i,\unicode[STIX]{x1D6FE}}\}_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
, then these integers are all zero.
Proof. Let
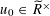 $u_{0}\in \widetilde{R}^{\times }$
be as in Lemma 5.8, and let
$u_{0}\in \widetilde{R}^{\times }$
be as in Lemma 5.8, and let
![]() $\unicode[STIX]{x1D71B}$
be a uniformizer of
$\unicode[STIX]{x1D71B}$
be a uniformizer of
![]() $R$
(which does not have to be the same as the uniformizer in the proof of Lemma 5.8). Let us choose elements
$R$
(which does not have to be the same as the uniformizer in the proof of Lemma 5.8). Let us choose elements
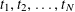 $t_{1},t_{2},\ldots ,t_{N}$
in
$t_{1},t_{2},\ldots ,t_{N}$
in
![]() $K^{\times }$
that are algebraically independent over the subfield
$K^{\times }$
that are algebraically independent over the subfield
![]() $\widetilde{K}_{0}$
of
$\widetilde{K}_{0}$
of
![]() $\widetilde{K}$
generated by
$\widetilde{K}$
generated by
![]() $\unicode[STIX]{x1D71B}$
and the finite subset
$\unicode[STIX]{x1D71B}$
and the finite subset
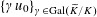 $\{\unicode[STIX]{x1D6FE}u_{0}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
over its prime subfield. This is possible because the transcendence degree of
$\{\unicode[STIX]{x1D6FE}u_{0}\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
over its prime subfield. This is possible because the transcendence degree of
![]() $\widetilde{K}$
over its prime subfield is (uncountably) infinite. For each
$\widetilde{K}$
over its prime subfield is (uncountably) infinite. For each
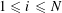 $1\leqslant i\leqslant N$
, up to replacing
$1\leqslant i\leqslant N$
, up to replacing
![]() $t_{i}$
with a suitable multiple by a power of
$t_{i}$
with a suitable multiple by a power of
![]() $\unicode[STIX]{x1D71B}$
, we may assume that
$\unicode[STIX]{x1D71B}$
, we may assume that
![]() $t_{i}\in R^{\times }$
. Let
$t_{i}\in R^{\times }$
. Let
 $$\begin{eqnarray}u_{i}:=1+u_{0}t_{i}\unicode[STIX]{x1D71B}\in \widetilde{R}^{\times },\end{eqnarray}$$
$$\begin{eqnarray}u_{i}:=1+u_{0}t_{i}\unicode[STIX]{x1D71B}\in \widetilde{R}^{\times },\end{eqnarray}$$
so that
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}u_{i}=1+(\unicode[STIX]{x1D6FE}u_{0})t_{i}\unicode[STIX]{x1D71B}\in \widetilde{R}^{\times },\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}u_{i}=1+(\unicode[STIX]{x1D6FE}u_{0})t_{i}\unicode[STIX]{x1D71B}\in \widetilde{R}^{\times },\end{eqnarray}$$
for each
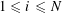 $1\leqslant i\leqslant N$
. We would like to show that these elements
$1\leqslant i\leqslant N$
. We would like to show that these elements
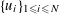 $\{u_{i}\}_{1\leqslant i\leqslant N}$
satisfy the requirement of the lemma; namely, if
$\{u_{i}\}_{1\leqslant i\leqslant N}$
satisfy the requirement of the lemma; namely, if
 $$\begin{eqnarray}\mathop{\prod }_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{i})^{c_{i,\unicode[STIX]{x1D6FE}}}=\mathop{\prod }_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(1+(\unicode[STIX]{x1D6FE}u_{0})t_{i}\unicode[STIX]{x1D71B})^{c_{i,\unicode[STIX]{x1D6FE}}}=1\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{i})^{c_{i,\unicode[STIX]{x1D6FE}}}=\mathop{\prod }_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(1+(\unicode[STIX]{x1D6FE}u_{0})t_{i}\unicode[STIX]{x1D71B})^{c_{i,\unicode[STIX]{x1D6FE}}}=1\end{eqnarray}$$
for some integers
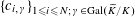 $\{c_{i,\unicode[STIX]{x1D6FE}}\}_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
, then these integers are all zero.
$\{c_{i,\unicode[STIX]{x1D6FE}}\}_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
, then these integers are all zero.
For all
![]() $i$
and
$i$
and
![]() $\unicode[STIX]{x1D6FE}$
, set
$\unicode[STIX]{x1D6FE}$
, set
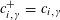 $c_{i,\unicode[STIX]{x1D6FE}}^{+}=c_{i,\unicode[STIX]{x1D6FE}}$
and
$c_{i,\unicode[STIX]{x1D6FE}}^{+}=c_{i,\unicode[STIX]{x1D6FE}}$
and
![]() $c_{i,\unicode[STIX]{x1D6FE}}^{-}=0$
when
$c_{i,\unicode[STIX]{x1D6FE}}^{-}=0$
when
![]() $c_{i,\unicode[STIX]{x1D6FE}}\geqslant 0$
, and set
$c_{i,\unicode[STIX]{x1D6FE}}\geqslant 0$
, and set
![]() $c_{i,\unicode[STIX]{x1D6FE}}^{+}=0$
and
$c_{i,\unicode[STIX]{x1D6FE}}^{+}=0$
and
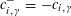 $c_{i,\unicode[STIX]{x1D6FE}}^{-}=-c_{i,\unicode[STIX]{x1D6FE}}$
when
$c_{i,\unicode[STIX]{x1D6FE}}^{-}=-c_{i,\unicode[STIX]{x1D6FE}}$
when
![]() $c_{i,\unicode[STIX]{x1D6FE}}\leqslant 0$
. Then the relation (5.11) implies that
$c_{i,\unicode[STIX]{x1D6FE}}\leqslant 0$
. Then the relation (5.11) implies that
 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(1+(\unicode[STIX]{x1D6FE}u_{0})t_{i}\unicode[STIX]{x1D71B})^{c_{i,\unicode[STIX]{x1D6FE}}^{+}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(1+(\unicode[STIX]{x1D6FE}u_{0})t_{i}\unicode[STIX]{x1D71B})^{c_{i,\unicode[STIX]{x1D6FE}}^{-}}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\prod }_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(1+(\unicode[STIX]{x1D6FE}u_{0})t_{i}\unicode[STIX]{x1D71B})^{c_{i,\unicode[STIX]{x1D6FE}}^{+}}\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\prod }_{1\leqslant i\leqslant N;\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(1+(\unicode[STIX]{x1D6FE}u_{0})t_{i}\unicode[STIX]{x1D71B})^{c_{i,\unicode[STIX]{x1D6FE}}^{-}}.\end{eqnarray}$$
Since
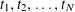 $t_{1},t_{2},\ldots ,t_{N}$
are algebraically independent over the subfield
$t_{1},t_{2},\ldots ,t_{N}$
are algebraically independent over the subfield
![]() $\widetilde{K}_{0}$
of
$\widetilde{K}_{0}$
of
![]() $\widetilde{K}$
, the relation (5.12) is possible only when the corresponding “polynomials” in
$\widetilde{K}$
, the relation (5.12) is possible only when the corresponding “polynomials” in
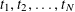 $t_{1},t_{2},\ldots ,t_{N}$
(with coefficients in
$t_{1},t_{2},\ldots ,t_{N}$
(with coefficients in
![]() $\widetilde{K}_{0}$
) on the two sides match. In particular, for each
$\widetilde{K}_{0}$
) on the two sides match. In particular, for each
 $1\leqslant i\leqslant N$
, by comparing the non-zero top degree “monomials” purely in
$1\leqslant i\leqslant N$
, by comparing the non-zero top degree “monomials” purely in
![]() $t_{i}$
(with coefficients in
$t_{i}$
(with coefficients in
![]() $\widetilde{K}_{0}$
) on the two sides, we have (by comparing exponents)
$\widetilde{K}_{0}$
) on the two sides, we have (by comparing exponents)
 $$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}c_{i,\unicode[STIX]{x1D6FE}}^{+}=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}c_{i,\unicode[STIX]{x1D6FE}}^{-}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}c_{i,\unicode[STIX]{x1D6FE}}^{+}=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}c_{i,\unicode[STIX]{x1D6FE}}^{-}\end{eqnarray}$$
in
![]() $\mathbb{Z}_{{\geqslant}0}$
, and have (by comparing coefficients, after canceling powers of
$\mathbb{Z}_{{\geqslant}0}$
, and have (by comparing coefficients, after canceling powers of
![]() $\unicode[STIX]{x1D71B}$
)
$\unicode[STIX]{x1D71B}$
)
 $$\begin{eqnarray}\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{0})^{c_{i,\unicode[STIX]{x1D6FE}}^{+}}=\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{0})^{c_{i,\unicode[STIX]{x1D6FE}}^{-}}\end{eqnarray}$$
$$\begin{eqnarray}\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{0})^{c_{i,\unicode[STIX]{x1D6FE}}^{+}}=\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}(\unicode[STIX]{x1D6FE}u_{0})^{c_{i,\unicode[STIX]{x1D6FE}}^{-}}\end{eqnarray}$$
in
![]() $\widetilde{R}^{\times }$
. By the assumption on
$\widetilde{R}^{\times }$
. By the assumption on
![]() $u_{0}$
(satisfying the requirement in Lemma 5.8), and by the definition of
$u_{0}$
(satisfying the requirement in Lemma 5.8), and by the definition of
![]() $c_{i,\unicode[STIX]{x1D6FE}}^{+}$
and
$c_{i,\unicode[STIX]{x1D6FE}}^{+}$
and
![]() $c_{i,\unicode[STIX]{x1D6FE}}^{-}$
, this last relation (5.13) forces all
$c_{i,\unicode[STIX]{x1D6FE}}^{-}$
, this last relation (5.13) forces all
![]() $c_{i,\unicode[STIX]{x1D6FE}}^{+}$
,
$c_{i,\unicode[STIX]{x1D6FE}}^{+}$
,
![]() $c_{i,\unicode[STIX]{x1D6FE}}^{-}$
, and
$c_{i,\unicode[STIX]{x1D6FE}}^{-}$
, and
![]() $c_{i,\unicode[STIX]{x1D6FE}}$
to be zero, for all
$c_{i,\unicode[STIX]{x1D6FE}}$
to be zero, for all
 $\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
, as desired.◻
$\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
, as desired.◻
Proposition 5.14. There exists a bimultiplicative pairing
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
as in (5.4) satisfying all the conditions in Propositions 5.3 and 5.5.
Proof. Let
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{0}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \mathbb{Z}\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{0}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \mathbb{Z}\end{eqnarray}$$
be any positive definite (symmetric) bilinear pairing. Let
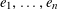 $e_{1},\ldots ,e_{n}$
denote the standard basis vectors of
$e_{1},\ldots ,e_{n}$
denote the standard basis vectors of
![]() $\mathbb{Z}^{n}$
, let
$\mathbb{Z}^{n}$
, let
![]() $\unicode[STIX]{x1D71B}$
be any element of
$\unicode[STIX]{x1D71B}$
be any element of
![]() $K^{\times }$
of positive valuation, and let
$K^{\times }$
of positive valuation, and let
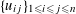 $\{u_{ij}\}_{1\leqslant i\leqslant j\leqslant n}$
be elements in
$\{u_{ij}\}_{1\leqslant i\leqslant j\leqslant n}$
be elements in
![]() $\widetilde{R}^{\times }$
that are multiplicatively Galois independent as in Lemma 5.10. Then we define a symmetric bimultiplicative pairing
$\widetilde{R}^{\times }$
that are multiplicatively Galois independent as in Lemma 5.10. Then we define a symmetric bimultiplicative pairing
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{1}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{1}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
by setting
 $$\begin{eqnarray}\langle e_{i},e_{j}\rangle _{1}:=u_{ij}\cdot \unicode[STIX]{x1D71B}^{\langle e_{i},e_{j}\rangle _{0}}\end{eqnarray}$$
$$\begin{eqnarray}\langle e_{i},e_{j}\rangle _{1}:=u_{ij}\cdot \unicode[STIX]{x1D71B}^{\langle e_{i},e_{j}\rangle _{0}}\end{eqnarray}$$
for all
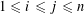 $1\leqslant i\leqslant j\leqslant n$
, and by extending the values of the pairing to the whole domain
$1\leqslant i\leqslant j\leqslant n$
, and by extending the values of the pairing to the whole domain
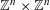 $\mathbb{Z}^{n}\times \mathbb{Z}^{n}$
by symmetry and bimultiplicativity. Next, we define a symmetric bimultiplicative pairing
$\mathbb{Z}^{n}\times \mathbb{Z}^{n}$
by symmetry and bimultiplicativity. Next, we define a symmetric bimultiplicative pairing
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{2}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{2}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
satisfying the Galois equivariance
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{2}=\unicode[STIX]{x1D6FE}\langle z,w\rangle _{2}\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{2}=\unicode[STIX]{x1D6FE}\langle z,w\rangle _{2}\end{eqnarray}$$
for all
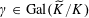 $\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
and
$\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
and
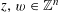 $z,w\in \mathbb{Z}^{n}$
, by setting
$z,w\in \mathbb{Z}^{n}$
, by setting
 $$\begin{eqnarray}\langle z,w\rangle _{2}:=\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}\unicode[STIX]{x1D6FE}^{-1}\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{1}\end{eqnarray}$$
$$\begin{eqnarray}\langle z,w\rangle _{2}:=\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}\unicode[STIX]{x1D6FE}^{-1}\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{1}\end{eqnarray}$$
for all
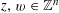 $z,w\in \mathbb{Z}^{n}$
. Finally, we define the desired bimultiplicative pairing
$z,w\in \mathbb{Z}^{n}$
. Finally, we define the desired bimultiplicative pairing
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
by setting
 $$\begin{eqnarray}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:=\langle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z),w\rangle _{2}\end{eqnarray}$$
$$\begin{eqnarray}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:=\langle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z),w\rangle _{2}\end{eqnarray}$$
for all
 $z,w\in \mathbb{Z}^{n}$
, where
$z,w\in \mathbb{Z}^{n}$
, where
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
is as in (5.1). Then
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
is as in (5.1). Then
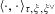 $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
satisfies the three conditions (1), (2), and (3) in Proposition 5.3 by the symmetry and positive definiteness of
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
satisfies the three conditions (1), (2), and (3) in Proposition 5.3 by the symmetry and positive definiteness of
![]() $\langle \cdot ,\cdot \rangle _{0}$
; by the definitions of the pairings
$\langle \cdot ,\cdot \rangle _{0}$
; by the definitions of the pairings
![]() $\langle \cdot ,\cdot \rangle _{1}$
and
$\langle \cdot ,\cdot \rangle _{1}$
and
![]() $\langle \cdot ,\cdot \rangle _{2}$
; by the choices of
$\langle \cdot ,\cdot \rangle _{2}$
; by the choices of
![]() $\unicode[STIX]{x1D71B}$
(of positive valuation in
$\unicode[STIX]{x1D71B}$
(of positive valuation in
![]() $\widetilde{K}^{\times }$
) and
$\widetilde{K}^{\times }$
) and
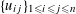 $\{u_{ij}\}_{1\leqslant i\leqslant j\leqslant n}$
(of zero valuation in
$\{u_{ij}\}_{1\leqslant i\leqslant j\leqslant n}$
(of zero valuation in
![]() $\widetilde{K}^{\times }$
); and by Lemma 5.2 and the relations (5.15) and (5.17).
$\widetilde{K}^{\times }$
); and by Lemma 5.2 and the relations (5.15) and (5.17).
It remains to show that
 $\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
(as in (5.6)) for all non-zero
$\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
(as in (5.6)) for all non-zero
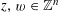 $z,w\in \mathbb{Z}^{n}$
. Since
$z,w\in \mathbb{Z}^{n}$
. Since
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
is an embedding, by the defining relation (5.17), it suffices to show that
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
is an embedding, by the defining relation (5.17), it suffices to show that
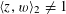 $\langle z,w\rangle _{2}\neq 1$
for all non-zero
$\langle z,w\rangle _{2}\neq 1$
for all non-zero
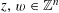 $z,w\in \mathbb{Z}^{n}$
. By the choice of
$z,w\in \mathbb{Z}^{n}$
. By the choice of
 $\{u_{ij}\}_{1\leqslant i\leqslant j\leqslant n}$
, the terms in the product (5.16) indexed by different elements
$\{u_{ij}\}_{1\leqslant i\leqslant j\leqslant n}$
, the terms in the product (5.16) indexed by different elements
![]() $\unicode[STIX]{x1D6FE}$
have multiplicatively independent values (up to powers of
$\unicode[STIX]{x1D6FE}$
have multiplicatively independent values (up to powers of
![]() $\unicode[STIX]{x1D71B}$
), and so it suffices to show that
$\unicode[STIX]{x1D71B}$
), and so it suffices to show that
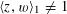 $\langle z,w\rangle _{1}\neq 1$
for all non-zero
$\langle z,w\rangle _{1}\neq 1$
for all non-zero
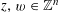 $z,w\in \mathbb{Z}^{n}$
. Suppose, to the contrary, that there are some
$z,w\in \mathbb{Z}^{n}$
. Suppose, to the contrary, that there are some
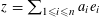 $z=\sum _{1\leqslant i\leqslant n}a_{i}e_{i}$
and
$z=\sum _{1\leqslant i\leqslant n}a_{i}e_{i}$
and
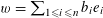 $w=\sum _{1\leqslant i\leqslant n}b_{i}e_{i}$
, where
$w=\sum _{1\leqslant i\leqslant n}b_{i}e_{i}$
, where
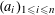 $(a_{i})_{1\leqslant i\leqslant n}$
and
$(a_{i})_{1\leqslant i\leqslant n}$
and
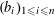 $(b_{i})_{1\leqslant i\leqslant n}$
are non-zero
$(b_{i})_{1\leqslant i\leqslant n}$
are non-zero
![]() $n$
-tuples of integers, such that
$n$
-tuples of integers, such that
 $\langle z,w\rangle _{1}=1$
. Then we have
$\langle z,w\rangle _{1}=1$
. Then we have
 $$\begin{eqnarray}\biggl(\mathop{\prod }_{1\leqslant i\leqslant n}\langle e_{i},e_{i}\rangle _{1}^{a_{i}b_{i}}\biggr)\cdot \biggl(\mathop{\prod }_{1\leqslant i<j\leqslant n}\langle e_{i},e_{j}\rangle _{1}^{a_{i}b_{j}+b_{i}a_{j}}\biggr)=1\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\mathop{\prod }_{1\leqslant i\leqslant n}\langle e_{i},e_{i}\rangle _{1}^{a_{i}b_{i}}\biggr)\cdot \biggl(\mathop{\prod }_{1\leqslant i<j\leqslant n}\langle e_{i},e_{j}\rangle _{1}^{a_{i}b_{j}+b_{i}a_{j}}\biggr)=1\end{eqnarray}$$
in
![]() $\widetilde{K}^{\times }$
, which implies that
$\widetilde{K}^{\times }$
, which implies that
 $$\begin{eqnarray}\biggl(\mathop{\prod }_{1\leqslant i\leqslant n}u_{ii}^{a_{i}b_{i}}\biggr)\cdot \biggl(\mathop{\prod }_{1\leqslant i<j\leqslant n}u_{ij}^{a_{i}b_{j}+b_{i}a_{j}}\biggr)=1\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\mathop{\prod }_{1\leqslant i\leqslant n}u_{ii}^{a_{i}b_{i}}\biggr)\cdot \biggl(\mathop{\prod }_{1\leqslant i<j\leqslant n}u_{ij}^{a_{i}b_{j}+b_{i}a_{j}}\biggr)=1\end{eqnarray}$$
in
![]() $\widetilde{R}^{\times }$
(by pulling out all powers of
$\widetilde{R}^{\times }$
(by pulling out all powers of
![]() $\unicode[STIX]{x1D71B}$
). By the choices of
$\unicode[STIX]{x1D71B}$
). By the choices of
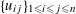 $\{u_{ij}\}_{1\leqslant i\leqslant j\leqslant n}$
again, the identity (5.18) is possible only when
$\{u_{ij}\}_{1\leqslant i\leqslant j\leqslant n}$
again, the identity (5.18) is possible only when
 $$\begin{eqnarray}a_{i}b_{j}+b_{i}a_{j}=0\end{eqnarray}$$
$$\begin{eqnarray}a_{i}b_{j}+b_{i}a_{j}=0\end{eqnarray}$$
in
![]() $\mathbb{Z}$
for all
$\mathbb{Z}$
for all
 $1\leqslant i\leqslant j\leqslant n$
. Let
$1\leqslant i\leqslant j\leqslant n$
. Let
![]() $i_{0}$
(respectively
$i_{0}$
(respectively
![]() $j_{0}$
) be the smallest index
$j_{0}$
) be the smallest index
![]() $i$
(respectively
$i$
(respectively
![]() $j$
) such that
$j$
) such that
![]() $a_{i}\neq 0$
(respectively
$a_{i}\neq 0$
(respectively
![]() $b_{j}\neq 0$
), which exists by assumption. But then
$b_{j}\neq 0$
), which exists by assumption. But then
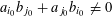 $a_{i_{0}}b_{j_{0}}+a_{j_{0}}b_{i_{0}}\neq 0$
. This contradicts the condition (5.19), as desired.◻
$a_{i_{0}}b_{j_{0}}+a_{j_{0}}b_{i_{0}}\neq 0$
. This contradicts the condition (5.19), as desired.◻
Remark 5.20. If we start with any element
![]() $\unicode[STIX]{x1D71B}$
in
$\unicode[STIX]{x1D71B}$
in
![]() $K^{\times }$
of positive valuation and any positive definite (symmetric) bilinear pairing
$K^{\times }$
of positive valuation and any positive definite (symmetric) bilinear pairing
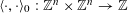 $\langle \cdot ,\cdot \rangle _{0}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \mathbb{Z}$
, and consider the Galois invariant pairing
$\langle \cdot ,\cdot \rangle _{0}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \mathbb{Z}$
, and consider the Galois invariant pairing
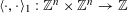 $\langle \cdot ,\cdot \rangle _{1}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \mathbb{Z}$
defined by the sum
$\langle \cdot ,\cdot \rangle _{1}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \mathbb{Z}$
defined by the sum
 $$\begin{eqnarray}\langle z,w\rangle _{1}:=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{0},\end{eqnarray}$$
$$\begin{eqnarray}\langle z,w\rangle _{1}:=\mathop{\sum }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{0},\end{eqnarray}$$
then the bimultiplicative pairing
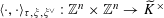 $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }$
defined by
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow \widetilde{K}^{\times }$
defined by
 $$\begin{eqnarray}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:=\unicode[STIX]{x1D71B}^{\langle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z),w\rangle _{1}}\in K^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:=\unicode[STIX]{x1D71B}^{\langle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z),w\rangle _{1}}\in K^{\times }\end{eqnarray}$$
satisfies all the conditions in Proposition 5.3. However, by completion of squares, there exists
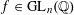 $f\in \operatorname{GL}_{n}(\mathbb{Q})$
such that
$f\in \operatorname{GL}_{n}(\mathbb{Q})$
such that
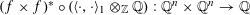 $(f\times f)^{\ast }\circ (\langle \cdot ,\cdot \rangle _{1}\otimes _{\mathbb{Z}}\mathbb{Q}):\mathbb{Q}^{n}\times \mathbb{Q}^{n}\rightarrow \mathbb{Q}$
decomposes as an orthogonal direct sum of pairings over one-dimensional subspaces. Thus, when
$(f\times f)^{\ast }\circ (\langle \cdot ,\cdot \rangle _{1}\otimes _{\mathbb{Z}}\mathbb{Q}):\mathbb{Q}^{n}\times \mathbb{Q}^{n}\rightarrow \mathbb{Q}$
decomposes as an orthogonal direct sum of pairings over one-dimensional subspaces. Thus, when
![]() $n>1$
, no pairing
$n>1$
, no pairing
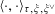 $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
defined as above can possibly satisfy the condition in Proposition 5.5. Furthermore, by Proposition 5.3, and by the functoriality in the theory of degeneration in §4, some non-zero multiple of
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
defined as above can possibly satisfy the condition in Proposition 5.5. Furthermore, by Proposition 5.3, and by the functoriality in the theory of degeneration in §4, some non-zero multiple of
![]() $f$
defines an isogeny between
$f$
defines an isogeny between
![]() $G_{\widetilde{\unicode[STIX]{x1D702}}}$
and a product of one-dimensional abelian varieties (i.e. elliptic curves) over
$G_{\widetilde{\unicode[STIX]{x1D702}}}$
and a product of one-dimensional abelian varieties (i.e. elliptic curves) over
![]() $\widetilde{\unicode[STIX]{x1D702}}$
. In particular, when
$\widetilde{\unicode[STIX]{x1D702}}$
. In particular, when
![]() $n>1$
, no
$n>1$
, no
![]() $G_{\unicode[STIX]{x1D702}}$
thus obtained can be absolutely simple.
$G_{\unicode[STIX]{x1D702}}$
thus obtained can be absolutely simple.
Remark 5.21. If we consider only
![]() $K^{\times }$
-valued pairings
$K^{\times }$
-valued pairings
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow K^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{n}\times \mathbb{Z}^{n}\rightarrow K^{\times }\end{eqnarray}$$
satisfying all the conditions in Proposition 5.3, then the Galois equivariance condition (1) there becomes the simpler Galois invariance condition
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\end{eqnarray}$$
for all
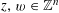 $z,w\in \mathbb{Z}^{n}$
and
$z,w\in \mathbb{Z}^{n}$
and
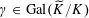 $\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
. Since
$\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
. Since
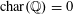 $\operatorname{char}(\mathbb{Q})=0$
, and since
$\operatorname{char}(\mathbb{Q})=0$
, and since
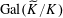 $\operatorname{Gal}(\widetilde{K}/K)$
is finite, the (finite-dimensional)
$\operatorname{Gal}(\widetilde{K}/K)$
is finite, the (finite-dimensional)
![]() $\mathbb{Q}$
-subalgebra
$\mathbb{Q}$
-subalgebra
![]() $B$
of
$B$
of
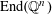 $\operatorname{End}(\mathbb{Q}^{n})$
generated by the images
$\operatorname{End}(\mathbb{Q}^{n})$
generated by the images
 $\{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
issemisimple (see, for example, [Reference Curtis and Reiner4, Theorem 15.6 and (25.8)]), and the
$\{\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})\}_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}$
issemisimple (see, for example, [Reference Curtis and Reiner4, Theorem 15.6 and (25.8)]), and the
![]() $\mathbb{Z}$
-subalgebra
$\mathbb{Z}$
-subalgebra
![]() ${\mathcal{O}}$
of
${\mathcal{O}}$
of
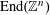 $\operatorname{End}(\mathbb{Z}^{n})$
generated by the same images is an order in
$\operatorname{End}(\mathbb{Z}^{n})$
generated by the same images is an order in
![]() $B$
. The anti-automorphism
$B$
. The anti-automorphism
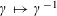 $\unicode[STIX]{x1D6FE}\mapsto \unicode[STIX]{x1D6FE}^{-1}$
of
$\unicode[STIX]{x1D6FE}\mapsto \unicode[STIX]{x1D6FE}^{-1}$
of
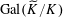 $\operatorname{Gal}(\widetilde{K}/K)$
induces an involution
$\operatorname{Gal}(\widetilde{K}/K)$
induces an involution
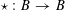 $\star :B\rightarrow B$
stabilizing
$\star :B\rightarrow B$
stabilizing
![]() ${\mathcal{O}}$
, which is positive in the sense that
${\mathcal{O}}$
, which is positive in the sense that
 $\operatorname{Tr}_{B/\mathbb{Q}}(bb^{\star })>0$
for all non-zero
$\operatorname{Tr}_{B/\mathbb{Q}}(bb^{\star })>0$
for all non-zero
![]() $b\in B$
. (Such orders and algebras with positive involutions are exactly the ones considered in the context of endomorphisms of abelian varieties; see §7 below.) Then the above condition (5.22) can be rewritten as
$b\in B$
. (Such orders and algebras with positive involutions are exactly the ones considered in the context of endomorphisms of abelian varieties; see §7 below.) Then the above condition (5.22) can be rewritten as
 $$\begin{eqnarray}\langle bz,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle z,b^{\star }w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\end{eqnarray}$$
$$\begin{eqnarray}\langle bz,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle z,b^{\star }w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\end{eqnarray}$$
for all
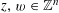 $z,w\in \mathbb{Z}^{n}$
and
$z,w\in \mathbb{Z}^{n}$
and
![]() $b\in {\mathcal{O}}$
. By Proposition 5.3, and by the functoriality in the theory of degeneration in §4, we obtain an injective homomorphism
$b\in {\mathcal{O}}$
. By Proposition 5.3, and by the functoriality in the theory of degeneration in §4, we obtain an injective homomorphism
 $i_{\widetilde{S}}:{\mathcal{O}}\rightarrow \operatorname{End}_{\widetilde{S}}(G_{\widetilde{S}})$
, whose restriction
$i_{\widetilde{S}}:{\mathcal{O}}\rightarrow \operatorname{End}_{\widetilde{S}}(G_{\widetilde{S}})$
, whose restriction
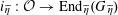 $i_{\widetilde{\unicode[STIX]{x1D702}}}:{\mathcal{O}}\rightarrow \operatorname{End}_{\widetilde{\unicode[STIX]{x1D702}}}(G_{\widetilde{\unicode[STIX]{x1D702}}})$
satisfies the Rosati condition defined by the polarization
$i_{\widetilde{\unicode[STIX]{x1D702}}}:{\mathcal{O}}\rightarrow \operatorname{End}_{\widetilde{\unicode[STIX]{x1D702}}}(G_{\widetilde{\unicode[STIX]{x1D702}}})$
satisfies the Rosati condition defined by the polarization
![]() $\unicode[STIX]{x1D706}_{\widetilde{\unicode[STIX]{x1D702}}}$
and by the involution
$\unicode[STIX]{x1D706}_{\widetilde{\unicode[STIX]{x1D702}}}$
and by the involution
![]() $\star$
. (See the theory with endomorphisms in §7 below. But beware that we cannot descend
$\star$
. (See the theory with endomorphisms in §7 below. But beware that we cannot descend
![]() $i_{\widetilde{S}}$
to a homomorphism
$i_{\widetilde{S}}$
to a homomorphism
 $i:{\mathcal{O}}\rightarrow \operatorname{End}_{S}(G)$
in general.) When
$i:{\mathcal{O}}\rightarrow \operatorname{End}_{S}(G)$
in general.) When
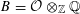 $B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is not a division algebra (which is quite often the case), the injective homomorphism
$B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is not a division algebra (which is quite often the case), the injective homomorphism
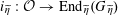 $i_{\widetilde{\unicode[STIX]{x1D702}}}:{\mathcal{O}}\rightarrow \operatorname{End}_{\widetilde{\unicode[STIX]{x1D702}}}(G_{\widetilde{\unicode[STIX]{x1D702}}})$
forces
$i_{\widetilde{\unicode[STIX]{x1D702}}}:{\mathcal{O}}\rightarrow \operatorname{End}_{\widetilde{\unicode[STIX]{x1D702}}}(G_{\widetilde{\unicode[STIX]{x1D702}}})$
forces
![]() $G_{\widetilde{\unicode[STIX]{x1D702}}}$
to be isogenous to a non-trivial product of abelian varieties of smaller dimensions, in which case
$G_{\widetilde{\unicode[STIX]{x1D702}}}$
to be isogenous to a non-trivial product of abelian varieties of smaller dimensions, in which case
![]() $G_{\unicode[STIX]{x1D702}}$
cannot be absolutely simple.
$G_{\unicode[STIX]{x1D702}}$
cannot be absolutely simple.
Example 5.23. In the context of Remark 5.21, suppose
![]() $\widetilde{k}$
is a quadratic extension of
$\widetilde{k}$
is a quadratic extension of
![]() $k$
, and suppose
$k$
, and suppose
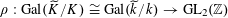 $\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\cong \operatorname{Gal}(\widetilde{k}/k)\rightarrow \operatorname{GL}_{2}(\mathbb{Z})$
maps the non-trivial element of
$\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\cong \operatorname{Gal}(\widetilde{k}/k)\rightarrow \operatorname{GL}_{2}(\mathbb{Z})$
maps the non-trivial element of
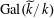 $\operatorname{Gal}(\widetilde{k}/k)$
to the automorphism
$\operatorname{Gal}(\widetilde{k}/k)$
to the automorphism
![]() $\unicode[STIX]{x1D70D}$
of
$\unicode[STIX]{x1D70D}$
of
![]() $\mathbb{Z}^{2}$
swapping the two factors. Then
$\mathbb{Z}^{2}$
swapping the two factors. Then
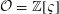 ${\mathcal{O}}=\mathbb{Z}[\unicode[STIX]{x1D70D}]$
, and
${\mathcal{O}}=\mathbb{Z}[\unicode[STIX]{x1D70D}]$
, and
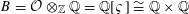 $B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}=\mathbb{Q}[\unicode[STIX]{x1D70D}]\cong \mathbb{Q}\times \mathbb{Q}$
is a product of two fields. Consequently, every
$B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}=\mathbb{Q}[\unicode[STIX]{x1D70D}]\cong \mathbb{Q}\times \mathbb{Q}$
is a product of two fields. Consequently, every
![]() $K^{\times }$
-valued pairing
$K^{\times }$
-valued pairing
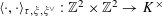 $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{2}\times \mathbb{Z}^{2}\rightarrow K^{\times }$
satisfying all the conditions in Proposition 5.3 defines an object
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:\mathbb{Z}^{2}\times \mathbb{Z}^{2}\rightarrow K^{\times }$
satisfying all the conditions in Proposition 5.3 defines an object
![]() $(G,\unicode[STIX]{x1D706})$
in
$(G,\unicode[STIX]{x1D706})$
in
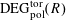 $\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
such that
$\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
such that
![]() $G_{\widetilde{\unicode[STIX]{x1D702}}}$
is isogenous to the product of two one-dimensional abelian varieties (i.e. elliptic curves) over
$G_{\widetilde{\unicode[STIX]{x1D702}}}$
is isogenous to the product of two one-dimensional abelian varieties (i.e. elliptic curves) over
![]() $\widetilde{\unicode[STIX]{x1D702}}$
, in which case
$\widetilde{\unicode[STIX]{x1D702}}$
, in which case
![]() $G_{\unicode[STIX]{x1D702}}$
cannot be absolutely simple.
$G_{\unicode[STIX]{x1D702}}$
cannot be absolutely simple.
6 Proof of main theorem
Now we are ready to prove our main theorem. Let us first state and prove a finer statement for the case of degenerations over complete discrete valuation rings.
Theorem 6.1. Let
![]() $R$
,
$R$
,
![]() $k$
,
$k$
,
![]() $K$
,
$K$
,
![]() $S$
,
$S$
,
![]() $s$
, and
$s$
, and
![]() $\unicode[STIX]{x1D702}$
be as in the beginning of §4. Given any tori
$\unicode[STIX]{x1D702}$
be as in the beginning of §4. Given any tori
![]() $T_{s}$
and
$T_{s}$
and
![]() $T_{s}^{\vee }$
with character groups
$T_{s}^{\vee }$
with character groups
![]() $\text{}\underline{X}_{s}$
and
$\text{}\underline{X}_{s}$
and
![]() $\text{}\underline{Y}_{s}$
, respectively, and an embedding
$\text{}\underline{Y}_{s}$
, respectively, and an embedding
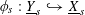 $\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
inducing an isogeny
$\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
inducing an isogeny
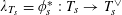 $\unicode[STIX]{x1D706}_{T_{s}}=\unicode[STIX]{x1D719}_{s}^{\ast }:T_{s}\rightarrow T_{s}^{\vee }$
(as in the beginning of §5), there exists an object
$\unicode[STIX]{x1D706}_{T_{s}}=\unicode[STIX]{x1D719}_{s}^{\ast }:T_{s}\rightarrow T_{s}^{\vee }$
(as in the beginning of §5), there exists an object
![]() $(G,\unicode[STIX]{x1D706})$
in
$(G,\unicode[STIX]{x1D706})$
in
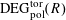 $\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
(see Definition 4.1) such that
$\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
(see Definition 4.1) such that
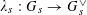 $\unicode[STIX]{x1D706}_{s}:G_{s}\rightarrow G_{s}^{\vee }$
can be identified with
$\unicode[STIX]{x1D706}_{s}:G_{s}\rightarrow G_{s}^{\vee }$
can be identified with
 $\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some isomorphisms
$\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some isomorphisms
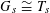 $G_{s}\cong T_{s}$
and
$G_{s}\cong T_{s}$
and
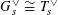 $G_{s}^{\vee }\cong T_{s}^{\vee }$
over
$G_{s}^{\vee }\cong T_{s}^{\vee }$
over
![]() $s$
), and such that
$s$
), and such that
![]() $G_{\unicode[STIX]{x1D702}}$
is absolute simple.
$G_{\unicode[STIX]{x1D702}}$
is absolute simple.
Thus, the case (a) of Theorem 1.3 over complete discrete valuation rings with residue field
![]() $k$
follows from the following.
$k$
follows from the following.
Corollary 6.2. Given any field
![]() $k$
and any complete discrete valuation ring
$k$
and any complete discrete valuation ring
![]() $R$
with residue field
$R$
with residue field
![]() $k$
, any torus over
$k$
, any torus over
![]() $k$
can be realized as the special fiber of some semi-abelian scheme over
$k$
can be realized as the special fiber of some semi-abelian scheme over
![]() $R$
whose generic fiber is an absolutely simple abelian variety (which can be principally polarized) over
$R$
whose generic fiber is an absolutely simple abelian variety (which can be principally polarized) over
![]() $K$
.
$K$
.
Proof. By Remark 4.3, it suffices to prove the assertion for polarized abelian varieties, and so it suffices to apply Theorem 6.1 to the given torus over
![]() $k$
, with the isogeny given by the identity morphism from this torus to itself.◻
$k$
, with the isogeny given by the identity morphism from this torus to itself.◻
It still remains to prove the cases (b) and (c) of Theorem 1.3. We shall deduce them from the case (a) of Theorem 1.3 over complete discrete valuation rings, by slightly modifying the argument in [Reference Faltings and Chai7, Ch. IV, §4] based on Artin’s approximation. Let us retain the setting of Theorem 6.1, but with the more specific choice that
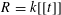 $R=k[[t]]$
(respectively the Witt vectors
$R=k[[t]]$
(respectively the Witt vectors
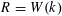 $R=W(k)$
) in case (b) (respectively in case (c)). Let
$R=W(k)$
) in case (b) (respectively in case (c)). Let
![]() $I$
denote the maximal ideal of
$I$
denote the maximal ideal of
![]() $R$
.
$R$
.
Let
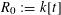 $R_{0}:=k[t]$
(respectively a number ring with an absolutely unramified prime ideal
$R_{0}:=k[t]$
(respectively a number ring with an absolutely unramified prime ideal
![]() $\mathfrak{P}$
with residue field
$\mathfrak{P}$
with residue field
![]() $k$
, so that
$k$
, so that
![]() $R_{0}$
is embedded in
$R_{0}$
is embedded in
![]() $R$
via
$R$
via
![]() $\mathfrak{P}$
-adic completion), and let
$\mathfrak{P}$
-adic completion), and let
![]() $I_{0}$
denote the ideal
$I_{0}$
denote the ideal
![]() $(t)$
(respectively
$(t)$
(respectively
![]() $\mathfrak{P}$
) of
$\mathfrak{P}$
) of
![]() $R_{0}$
. Let
$R_{0}$
. Let
![]() $R_{1}$
be the Henselization of
$R_{1}$
be the Henselization of
![]() $R_{0}$
at
$R_{0}$
at
![]() $I_{0}$
, which is canonically a subring of
$I_{0}$
, which is canonically a subring of
![]() $R$
. (See, for example, [Reference Grothendieck and Dieudonné9, IV-4, 18.6].) Let
$R$
. (See, for example, [Reference Grothendieck and Dieudonné9, IV-4, 18.6].) Let
![]() $I_{1}$
denote the ideal of
$I_{1}$
denote the ideal of
![]() $R_{1}$
generated by
$R_{1}$
generated by
![]() $I_{0}$
, so that the maximal ideal
$I_{0}$
, so that the maximal ideal
![]() $I$
of
$I$
of
![]() $R$
is generated by
$R$
is generated by
![]() $I_{1}$
. For
$I_{1}$
. For
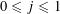 $0\leqslant j\leqslant 1$
, we shall denote the fraction field of
$0\leqslant j\leqslant 1$
, we shall denote the fraction field of
![]() $R_{j}$
by
$R_{j}$
by
![]() $K_{j}$
; define
$K_{j}$
; define
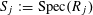 $S_{j}:=\operatorname{Spec}(R_{j})$
and
$S_{j}:=\operatorname{Spec}(R_{j})$
and
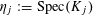 $\unicode[STIX]{x1D702}_{j}:=\operatorname{Spec}(K_{j})$
; and, by abuse of notation, still denote by
$\unicode[STIX]{x1D702}_{j}:=\operatorname{Spec}(K_{j})$
; and, by abuse of notation, still denote by
![]() $s$
the closed points
$s$
the closed points
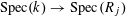 $\operatorname{Spec}(k)\rightarrow \operatorname{Spec}(R_{j})$
defined by
$\operatorname{Spec}(k)\rightarrow \operatorname{Spec}(R_{j})$
defined by
![]() $I_{j}$
.
$I_{j}$
.
Proposition 6.3. Suppose
![]() $R_{2}$
is a subalgebra of
$R_{2}$
is a subalgebra of
![]() $R$
that is of finite type over
$R$
that is of finite type over
![]() $R_{1}$
. Then, given any integer
$R_{1}$
. Then, given any integer
![]() $m\geqslant 1$
, the natural inclusion
$m\geqslant 1$
, the natural inclusion
 $R_{1}{\hookrightarrow}R_{2}$
has some (homomorphic) section
$R_{1}{\hookrightarrow}R_{2}$
has some (homomorphic) section
 $R_{2}\rightarrow R_{1}$
(depending on
$R_{2}\rightarrow R_{1}$
(depending on
![]() $m$
) such that the composition
$m$
) such that the composition
 $R_{2}\rightarrow R_{1}{\hookrightarrow}R$
coincides with the natural inclusion
$R_{2}\rightarrow R_{1}{\hookrightarrow}R$
coincides with the natural inclusion
 $R_{2}{\hookrightarrow}R$
after reduction modulo
$R_{2}{\hookrightarrow}R$
after reduction modulo
![]() $I^{m}$
in
$I^{m}$
in
![]() $R$
.
$R$
.
Proof. This follows from Artin’s approximation, as in [Reference Artin1, Theorem 1.10], because
![]() $R_{1}$
is the Henselization of the excellent Dedekind domain
$R_{1}$
is the Henselization of the excellent Dedekind domain
![]() $R_{0}$
at the maximal ideal
$R_{0}$
at the maximal ideal
![]() $I_{0}$
.◻
$I_{0}$
.◻
Theorem 6.4. Given any
![]() $(G,\unicode[STIX]{x1D706})$
in
$(G,\unicode[STIX]{x1D706})$
in
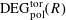 $\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
as in Theorem 6.1, there exists some
$\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
as in Theorem 6.1, there exists some
![]() $(G_{1},\unicode[STIX]{x1D706}_{1})$
in
$(G_{1},\unicode[STIX]{x1D706}_{1})$
in
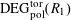 $\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R_{1})$
(see Remark 4.2) such that
$\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R_{1})$
(see Remark 4.2) such that
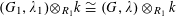 $(G_{1},\unicode[STIX]{x1D706}_{1})\otimes _{R_{1}}k\cong (G,\unicode[STIX]{x1D706})\otimes _{R_{1}}k$
, and such that the generic fiber
$(G_{1},\unicode[STIX]{x1D706}_{1})\otimes _{R_{1}}k\cong (G,\unicode[STIX]{x1D706})\otimes _{R_{1}}k$
, and such that the generic fiber
![]() $G_{1,\unicode[STIX]{x1D702}_{1}}$
is absolutely simple. Consequently, the special fiber
$G_{1,\unicode[STIX]{x1D702}_{1}}$
is absolutely simple. Consequently, the special fiber
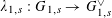 $\unicode[STIX]{x1D706}_{1,s}:G_{1,s}\rightarrow G_{1,s}^{\vee }$
of
$\unicode[STIX]{x1D706}_{1,s}:G_{1,s}\rightarrow G_{1,s}^{\vee }$
of
![]() $\unicode[STIX]{x1D706}_{0}$
can also be identified with
$\unicode[STIX]{x1D706}_{0}$
can also be identified with
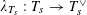 $\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some isomorphisms
$\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some isomorphisms
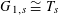 $G_{1,s}\cong T_{s}$
and
$G_{1,s}\cong T_{s}$
and
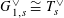 $G_{1,s}^{\vee }\cong T_{s}^{\vee }$
over
$G_{1,s}^{\vee }\cong T_{s}^{\vee }$
over
![]() $s$
).
$s$
).
These assertions remain true with
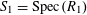 $S_{1}=\operatorname{Spec}(R_{1})$
replaced with some connected affine étale neighborhood
$S_{1}=\operatorname{Spec}(R_{1})$
replaced with some connected affine étale neighborhood
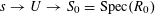 $s\rightarrow U\rightarrow S_{0}=\operatorname{Spec}(R_{0})$
of
$s\rightarrow U\rightarrow S_{0}=\operatorname{Spec}(R_{0})$
of
![]() $s$
.
$s$
.
Proof. Since
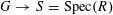 $G\rightarrow S=\operatorname{Spec}(R)$
and
$G\rightarrow S=\operatorname{Spec}(R)$
and
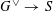 $G^{\vee }\rightarrow S$
are both of finite presentation, and since
$G^{\vee }\rightarrow S$
are both of finite presentation, and since
![]() $R$
is the filtering direct limit (union) of its normal subalgebras
$R$
is the filtering direct limit (union) of its normal subalgebras
![]() $R_{2}$
of finite type over
$R_{2}$
of finite type over
![]() $R_{1}$
, by [Reference Grothendieck and Dieudonné9, IV-3, 8.8.2], we may assume that there exist some such
$R_{1}$
, by [Reference Grothendieck and Dieudonné9, IV-3, 8.8.2], we may assume that there exist some such
![]() $R_{2}$
, some semi-abelian schemes
$R_{2}$
, some semi-abelian schemes
 $G_{2}\rightarrow S_{2}:=\operatorname{Spec}(R_{2})$
and
$G_{2}\rightarrow S_{2}:=\operatorname{Spec}(R_{2})$
and
 $G^{\vee }\rightarrow S_{2}$
, and some homomorphism
$G^{\vee }\rightarrow S_{2}$
, and some homomorphism
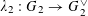 $\unicode[STIX]{x1D706}_{2}:G_{2}\rightarrow G_{2}^{\vee }$
such that
$\unicode[STIX]{x1D706}_{2}:G_{2}\rightarrow G_{2}^{\vee }$
such that
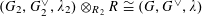 $(G_{2},G_{2}^{\vee },\unicode[STIX]{x1D706}_{2})\otimes _{R_{2}}R\cong (G,G^{\vee },\unicode[STIX]{x1D706})$
. Since the pullback of
$(G_{2},G_{2}^{\vee },\unicode[STIX]{x1D706}_{2})\otimes _{R_{2}}R\cong (G,G^{\vee },\unicode[STIX]{x1D706})$
. Since the pullback of
![]() $G_{2}$
and
$G_{2}$
and
![]() $G_{2}^{\vee }$
to
$G_{2}^{\vee }$
to
![]() $\unicode[STIX]{x1D702}$
are the absolutely simple abelian varieties
$\unicode[STIX]{x1D702}$
are the absolutely simple abelian varieties
![]() $G_{\unicode[STIX]{x1D702}}$
and
$G_{\unicode[STIX]{x1D702}}$
and
![]() $G_{\unicode[STIX]{x1D702}}^{\vee }$
, respectively, by [Reference Faltings and Chai7, Ch. I, Theorem 2.10] or [Reference Lan14, Ch. 3, Theorem 3.3.1.9]; and by [Reference Raynaud19, IX, 1.4], [Reference Faltings and Chai7, Ch. I, Proposition 2.7], or [Reference Lan14, Proposition 3.3.1.5], there exists a non-empty open subset
$G_{\unicode[STIX]{x1D702}}^{\vee }$
, respectively, by [Reference Faltings and Chai7, Ch. I, Theorem 2.10] or [Reference Lan14, Ch. 3, Theorem 3.3.1.9]; and by [Reference Raynaud19, IX, 1.4], [Reference Faltings and Chai7, Ch. I, Proposition 2.7], or [Reference Lan14, Proposition 3.3.1.5], there exists a non-empty open subset
![]() $W$
of
$W$
of
![]() $S_{2}$
such that
$S_{2}$
such that
![]() $G_{2}|_{W}$
and
$G_{2}|_{W}$
and
![]() $G_{2}^{\vee }|_{W}$
are abelian schemes whose fibers are all absolutely simple, and such that
$G_{2}^{\vee }|_{W}$
are abelian schemes whose fibers are all absolutely simple, and such that
![]() $\unicode[STIX]{x1D706}_{2}|_{W}$
is a polarization of abelian schemes. Suppose
$\unicode[STIX]{x1D706}_{2}|_{W}$
is a polarization of abelian schemes. Suppose
![]() $W$
is the complement of a closed subset of
$W$
is the complement of a closed subset of
![]() $S_{2}$
defined by some non-zero ideal
$S_{2}$
defined by some non-zero ideal
![]() $J_{2}$
of
$J_{2}$
of
![]() $R_{2}$
. Since
$R_{2}$
. Since
![]() $R_{2}\subset R$
, and since
$R_{2}\subset R$
, and since
![]() $R$
is noetherian and
$R$
is noetherian and
![]() $I$
-adically separated, there exists an integer
$I$
-adically separated, there exists an integer
![]() $m\geqslant 1$
such that
$m\geqslant 1$
such that
![]() $J_{2}$
is not contained in
$J_{2}$
is not contained in
![]() $I^{m}$
. By Proposition 6.3, there exists a section
$I^{m}$
. By Proposition 6.3, there exists a section
 $R_{2}\rightarrow R_{1}$
of
$R_{2}\rightarrow R_{1}$
of
 $R_{1}{\hookrightarrow}R_{2}$
such that the composition
$R_{1}{\hookrightarrow}R_{2}$
such that the composition
 $R_{2}\rightarrow R_{1}{\hookrightarrow}R$
coincides with the natural inclusion
$R_{2}\rightarrow R_{1}{\hookrightarrow}R$
coincides with the natural inclusion
 $R_{2}{\hookrightarrow}R$
after reduction modulo
$R_{2}{\hookrightarrow}R$
after reduction modulo
![]() $I^{m}$
in
$I^{m}$
in
![]() $R$
. Let
$R$
. Let
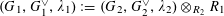 $(G_{1},G_{1}^{\vee },\unicode[STIX]{x1D706}_{1}):=(G_{2},G_{2}^{\vee },\unicode[STIX]{x1D706}_{2})\otimes _{R_{2}}R_{1}$
. Then
$(G_{1},G_{1}^{\vee },\unicode[STIX]{x1D706}_{1}):=(G_{2},G_{2}^{\vee },\unicode[STIX]{x1D706}_{2})\otimes _{R_{2}}R_{1}$
. Then
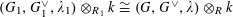 $(G_{1},G_{1}^{\vee },\unicode[STIX]{x1D706}_{1})\otimes _{R_{1}}k\cong (G,G^{\vee },\unicode[STIX]{x1D706})\otimes _{R}k$
because
$(G_{1},G_{1}^{\vee },\unicode[STIX]{x1D706}_{1})\otimes _{R_{1}}k\cong (G,G^{\vee },\unicode[STIX]{x1D706})\otimes _{R}k$
because
![]() $m\geqslant 1$
. Moreover,
$m\geqslant 1$
. Moreover,
![]() $J_{2}$
has non-zero image in
$J_{2}$
has non-zero image in
![]() $R_{1}$
under the section
$R_{1}$
under the section
 $R_{2}\rightarrow R_{1}$
above, and therefore the induced morphism
$R_{2}\rightarrow R_{1}$
above, and therefore the induced morphism
 $S_{1}=\operatorname{Spec}(R_{1})\rightarrow S_{2}=\operatorname{Spec}(R_{2})$
maps the generic point
$S_{1}=\operatorname{Spec}(R_{1})\rightarrow S_{2}=\operatorname{Spec}(R_{2})$
maps the generic point
![]() $\unicode[STIX]{x1D702}_{1}$
of
$\unicode[STIX]{x1D702}_{1}$
of
![]() $S_{1}$
to the above open subset
$S_{1}$
to the above open subset
![]() $W$
of
$W$
of
![]() $S_{2}$
. Hence,
$S_{2}$
. Hence,
![]() $(G_{1},\unicode[STIX]{x1D706}_{1})$
defines an object in
$(G_{1},\unicode[STIX]{x1D706}_{1})$
defines an object in
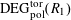 $\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R_{1})$
, and the generic fiber
$\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R_{1})$
, and the generic fiber
![]() $G_{1,\unicode[STIX]{x1D702}_{1}}$
is absolutely simple. This proves the first paragraph of the theorem.
$G_{1,\unicode[STIX]{x1D702}_{1}}$
is absolutely simple. This proves the first paragraph of the theorem.
Since
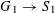 $G_{1}\rightarrow S_{1}$
and
$G_{1}\rightarrow S_{1}$
and
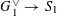 $G_{1}^{\vee }\rightarrow S_{1}$
are both of finite presentation, and since
$G_{1}^{\vee }\rightarrow S_{1}$
are both of finite presentation, and since
![]() $R_{1}$
is the filtering direct limit of the coordinate rings of all connected affine étale neighborhoods
$R_{1}$
is the filtering direct limit of the coordinate rings of all connected affine étale neighborhoods
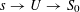 $s\rightarrow U\rightarrow S_{0}$
of
$s\rightarrow U\rightarrow S_{0}$
of
![]() $s$
, by [Reference Grothendieck and Dieudonné9, IV-3, 8.8.2] again, the second paragraph of the theorem follows from the first, as desired.◻
$s$
, by [Reference Grothendieck and Dieudonné9, IV-3, 8.8.2] again, the second paragraph of the theorem follows from the first, as desired.◻
Now, since an étale neighborhood
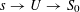 $s\rightarrow U\rightarrow S_{0}$
of
$s\rightarrow U\rightarrow S_{0}$
of
![]() $s$
is necessarily a smooth curve over
$s$
is necessarily a smooth curve over
![]() $k$
(with a
$k$
(with a
![]() $k$
-rational point lifting
$k$
-rational point lifting
![]() $s$
, which can still be denoted
$s$
, which can still be denoted
![]() $s$
) in case (b) (respectively an open subset of the spectrum of a number ring in case (c)), the cases (b) and (c) of Theorem 1.3 follow from the following.
$s$
) in case (b) (respectively an open subset of the spectrum of a number ring in case (c)), the cases (b) and (c) of Theorem 1.3 follow from the following.
Corollary 6.5. Given any field
![]() $k$
and any complete discrete valuation ring
$k$
and any complete discrete valuation ring
![]() $R$
with residue field
$R$
with residue field
![]() $k$
, any torus over
$k$
, any torus over
![]() $k$
can be realized as the special fiber of some semi-abelian scheme over some connected affine étale neighborhood
$k$
can be realized as the special fiber of some semi-abelian scheme over some connected affine étale neighborhood
 $s\rightarrow U\rightarrow S_{0}$
of
$s\rightarrow U\rightarrow S_{0}$
of
![]() $s$
that is generically an absolutely simple abelian variety (which can be principally polarized).
$s$
that is generically an absolutely simple abelian variety (which can be principally polarized).
Proof. As explained in the proof of Corollary 6.2, this follows from Theorem 6.4 just as Corollary 6.2 does from Theorem 6.1. (Alternatively, we could have approximated the semi-abelian scheme in Corollary 6.2 directly, using [Reference Grothendieck and Dieudonné9, IV-3, 8.8.2] and Proposition 6.3, as in the proof of Theorem 6.4.)◻
Remark 6.6. By the theory of Néron models (see, in particular, [Reference Bosch, Lütkebohmert and Raybaud3, Ch. 7, §7.4, Proposition 3]), the semi-abelian schemes in Corollaries 6.2 and 6.5 (where the base schemes are Dedekind domains) are exactly the identity components of the Néron models of their respective generic fibers.
7 Non-trivial endomorphisms
In this section, we investigate the analogue of Question 1.2 which requires additionally that the semi-abelian schemes are equipped with endomorphism structures.
Let
![]() ${\mathcal{O}}$
be an order in a finite-dimensional semisimple algebra
${\mathcal{O}}$
be an order in a finite-dimensional semisimple algebra
![]() $B$
over
$B$
over
![]() $\mathbb{Q}$
, and let
$\mathbb{Q}$
, and let
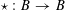 $\star :B\rightarrow B$
be a positive involution (i.e.
$\star :B\rightarrow B$
be a positive involution (i.e.
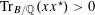 $\operatorname{Tr}_{B/\mathbb{Q}}(xx^{\star })>0$
for all non-zero
$\operatorname{Tr}_{B/\mathbb{Q}}(xx^{\star })>0$
for all non-zero
![]() $x$
in
$x$
in
![]() $B$
), which we assume to stabilize
$B$
), which we assume to stabilize
![]() ${\mathcal{O}}$
. All endomorphism algebras of abelian varieties over algebraically closed fields are necessarily of this form, with the involution
${\mathcal{O}}$
. All endomorphism algebras of abelian varieties over algebraically closed fields are necessarily of this form, with the involution
![]() $\star$
given by the Rosati involution induced by some polarization. (See, for example, [Reference Mumford17, §§20–21], which contains a treatment of Albert’s classification of finite-dimensional division algebras over
$\star$
given by the Rosati involution induced by some polarization. (See, for example, [Reference Mumford17, §§20–21], which contains a treatment of Albert’s classification of finite-dimensional division algebras over
![]() $\mathbb{Q}$
with positive involutions. See also [Reference Lan14, Propositions 1.2.1.13 and 1.2.1.14] for a summary of possibilities when
$\mathbb{Q}$
with positive involutions. See also [Reference Lan14, Propositions 1.2.1.13 and 1.2.1.14] for a summary of possibilities when
![]() $B$
is simple.)
$B$
is simple.)
Let us first expand the review of the theory of degeneration in §4. Let
![]() $R$
,
$R$
,
![]() $k$
,
$k$
,
![]() $K$
,
$K$
,
![]() $S$
,
$S$
,
![]() $s$
, and
$s$
, and
![]() $\unicode[STIX]{x1D702}$
be as in the beginning of §4.
$\unicode[STIX]{x1D702}$
be as in the beginning of §4.
Definition 7.1. With the setting as above, the category
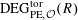 $\operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)$
has objects consisting of triples
$\operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)$
has objects consisting of triples
![]() $(G,\unicode[STIX]{x1D706},i)$
over
$(G,\unicode[STIX]{x1D706},i)$
over
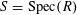 $S=\operatorname{Spec}(R)$
, where
$S=\operatorname{Spec}(R)$
, where
![]() $(G,\unicode[STIX]{x1D706})$
is an object in
$(G,\unicode[STIX]{x1D706})$
is an object in
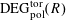 $\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
, and where
$\operatorname{DEG}_{\text{pol}}^{\text{tor}}(R)$
, and where
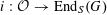 $i:{\mathcal{O}}\rightarrow \operatorname{End}_{S}(G)$
is a homomorphism satisfying the Rosati condition that
$i:{\mathcal{O}}\rightarrow \operatorname{End}_{S}(G)$
is a homomorphism satisfying the Rosati condition that
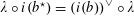 $\unicode[STIX]{x1D706}\circ i(b^{\star })=(i(b))^{\vee }\circ \unicode[STIX]{x1D706}$
as homomorphisms from
$\unicode[STIX]{x1D706}\circ i(b^{\star })=(i(b))^{\vee }\circ \unicode[STIX]{x1D706}$
as homomorphisms from
![]() $G$
to
$G$
to
![]() $G^{\vee }$
, where
$G^{\vee }$
, where
 $(i(b))^{\vee }:G^{\vee }\rightarrow G^{\vee }$
is the unique homomorphism (see [Reference Raynaud19, IX, 1.4], [Reference Faltings and Chai7, Ch. I, Proposition 2.7], or [Reference Lan14, Proposition 3.3.1.5]) extending the dual homomorphism
$(i(b))^{\vee }:G^{\vee }\rightarrow G^{\vee }$
is the unique homomorphism (see [Reference Raynaud19, IX, 1.4], [Reference Faltings and Chai7, Ch. I, Proposition 2.7], or [Reference Lan14, Proposition 3.3.1.5]) extending the dual homomorphism
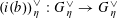 $(i(b))_{\unicode[STIX]{x1D702}}^{\vee }:G_{\unicode[STIX]{x1D702}}^{\vee }\rightarrow G_{\unicode[STIX]{x1D702}}^{\vee }$
of
$(i(b))_{\unicode[STIX]{x1D702}}^{\vee }:G_{\unicode[STIX]{x1D702}}^{\vee }\rightarrow G_{\unicode[STIX]{x1D702}}^{\vee }$
of
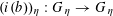 $(i(b))_{\unicode[STIX]{x1D702}}:G_{\unicode[STIX]{x1D702}}\rightarrow G_{\unicode[STIX]{x1D702}}$
, for all
$(i(b))_{\unicode[STIX]{x1D702}}:G_{\unicode[STIX]{x1D702}}\rightarrow G_{\unicode[STIX]{x1D702}}$
, for all
![]() $b\in {\mathcal{O}}$
.
$b\in {\mathcal{O}}$
.
Remark 7.2. As in the case of Definition 4.1 and Remark 4.2, the definition of pairs
![]() $(G,\unicode[STIX]{x1D706},i)$
as in Definition 4.1 extends verbatim to the case where
$(G,\unicode[STIX]{x1D706},i)$
as in Definition 4.1 extends verbatim to the case where
![]() $S$
is a noetherian normal local scheme.
$S$
is a noetherian normal local scheme.
By the theory of degeneration data (for polarized abelian schemes with endomorphism structures; see [Reference Lan14, §5.1.1; see, in particular, Theorem 5.1.1.4], with all abelian parts in the degenerations suppressed), there is an equivalence of categories
 $$\begin{eqnarray}\operatorname{M}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R):\;\operatorname{DD}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)\rightarrow \operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R):(\text{}\underline{X},\text{}\underline{Y},\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F})\mapsto (G,\unicode[STIX]{x1D706},i)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{M}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R):\;\operatorname{DD}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)\rightarrow \operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R):(\text{}\underline{X},\text{}\underline{Y},\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F})\mapsto (G,\unicode[STIX]{x1D706},i)\end{eqnarray}$$
realizing
![]() $(G,\unicode[STIX]{x1D706},i)$
(up to isomorphism) as the image of an object in
$(G,\unicode[STIX]{x1D706},i)$
(up to isomorphism) as the image of an object in
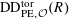 $\operatorname{DD}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)$
given by the following data.
$\operatorname{DD}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)$
given by the following data.
(1) The tuple
 $(\text{}\underline{X},\text{}\underline{Y},\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F})$
is an object in
$(\text{}\underline{X},\text{}\underline{Y},\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F})$
is an object in
 $\operatorname{DD}_{\text{pol}}^{\text{tor}}(R)$
, as in §4.
$\operatorname{DD}_{\text{pol}}^{\text{tor}}(R)$
, as in §4.(2) The étale shaves
 $\text{}\underline{X}$
and
$\text{}\underline{X}$
and
 $\text{}\underline{Y}$
are equipped with the structures of étale sheaves of left
$\text{}\underline{Y}$
are equipped with the structures of étale sheaves of left
 ${\mathcal{O}}$
-lattices (i.e.
${\mathcal{O}}$
-lattices (i.e.
 $\mathbb{Z}$
-lattices with left
$\mathbb{Z}$
-lattices with left
 ${\mathcal{O}}$
-module structures), and the embedding
${\mathcal{O}}$
-module structures), and the embedding
 $\unicode[STIX]{x1D719}:\text{}\underline{X}\rightarrow \text{}\underline{Y}$
is then
$\unicode[STIX]{x1D719}:\text{}\underline{X}\rightarrow \text{}\underline{Y}$
is then
 ${\mathcal{O}}$
-equivariant.
${\mathcal{O}}$
-equivariant.(3) The bimultiplicative homomorphism
 $\unicode[STIX]{x1D70F}:\text{}\underline{Y}_{\unicode[STIX]{x1D702}}\times \text{}\underline{X}_{\unicode[STIX]{x1D702}}\rightarrow \mathbb{G}_{\text{m},\unicode[STIX]{x1D702}}$
is compatible with the actions of
$\unicode[STIX]{x1D70F}:\text{}\underline{Y}_{\unicode[STIX]{x1D702}}\times \text{}\underline{X}_{\unicode[STIX]{x1D702}}\rightarrow \mathbb{G}_{\text{m},\unicode[STIX]{x1D702}}$
is compatible with the actions of
 ${\mathcal{O}}$
in the sense that
${\mathcal{O}}$
in the sense that
 $(b\times 1)^{\ast }\unicode[STIX]{x1D70F}=(1\times b^{\star })^{\ast }\unicode[STIX]{x1D70F}$
, for all
$(b\times 1)^{\ast }\unicode[STIX]{x1D70F}=(1\times b^{\star })^{\ast }\unicode[STIX]{x1D70F}$
, for all
 $b\in {\mathcal{O}}$
.
$b\in {\mathcal{O}}$
.
We say that
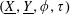 $(\text{}\underline{X},\text{}\underline{Y},\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F})$
is the degeneration data of
$(\text{}\underline{X},\text{}\underline{Y},\unicode[STIX]{x1D719},\unicode[STIX]{x1D70F})$
is the degeneration data of
![]() $(G,\unicode[STIX]{x1D706},i)$
.
$(G,\unicode[STIX]{x1D706},i)$
.
Suppose that we have tori
![]() $T_{s}$
and
$T_{s}$
and
![]() $T_{s}^{\vee }$
over
$T_{s}^{\vee }$
over
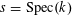 $s=\operatorname{Spec}(k)$
with character groups
$s=\operatorname{Spec}(k)$
with character groups
![]() $\text{}\underline{X}_{s}$
and
$\text{}\underline{X}_{s}$
and
![]() $\text{}\underline{Y}_{s}$
that are étale sheaves of left
$\text{}\underline{Y}_{s}$
that are étale sheaves of left
![]() ${\mathcal{O}}$
-lattices, together with an
${\mathcal{O}}$
-lattices, together with an
![]() ${\mathcal{O}}$
-equivariant embedding
${\mathcal{O}}$
-equivariant embedding
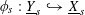 $\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
with finite cokernel, inducing an
$\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
with finite cokernel, inducing an
![]() ${\mathcal{O}}$
-equivariant isogeny
${\mathcal{O}}$
-equivariant isogeny
 $\unicode[STIX]{x1D706}_{T_{s}}:T_{s}{\twoheadrightarrow}T_{s}^{\vee }$
. By Lemma 3.1, the
$\unicode[STIX]{x1D706}_{T_{s}}:T_{s}{\twoheadrightarrow}T_{s}^{\vee }$
. By Lemma 3.1, the
![]() ${\mathcal{O}}$
-equivariant embedding
${\mathcal{O}}$
-equivariant embedding
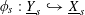 $\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
uniquely lifts to an
$\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
uniquely lifts to an
![]() ${\mathcal{O}}$
-equivariant embedding
${\mathcal{O}}$
-equivariant embedding
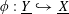 $\unicode[STIX]{x1D719}:\text{}\underline{Y}{\hookrightarrow}\text{}\underline{X}$
over
$\unicode[STIX]{x1D719}:\text{}\underline{Y}{\hookrightarrow}\text{}\underline{X}$
over
![]() $S$
of étale sheaves of left
$S$
of étale sheaves of left
![]() ${\mathcal{O}}$
-lattices with finite cokernel, inducing an
${\mathcal{O}}$
-lattices with finite cokernel, inducing an
![]() ${\mathcal{O}}$
-equivariant isogeny
${\mathcal{O}}$
-equivariant isogeny
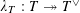 $\unicode[STIX]{x1D706}_{T}:T{\twoheadrightarrow}T^{\vee }$
(between isotrivial tori) lifting
$\unicode[STIX]{x1D706}_{T}:T{\twoheadrightarrow}T^{\vee }$
(between isotrivial tori) lifting
![]() $\unicode[STIX]{x1D706}_{T_{s}}$
. Let
$\unicode[STIX]{x1D706}_{T_{s}}$
. Let
![]() $\widetilde{S}$
, etc, be as in §§3 and 5 such that there are left
$\widetilde{S}$
, etc, be as in §§3 and 5 such that there are left
![]() ${\mathcal{O}}$
-lattices
${\mathcal{O}}$
-lattices
![]() $X$
and
$X$
and
![]() $Y$
, isomorphisms
$Y$
, isomorphisms
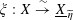 $\unicode[STIX]{x1D709}:X\stackrel{{\sim}}{\rightarrow }\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and
$\unicode[STIX]{x1D709}:X\stackrel{{\sim}}{\rightarrow }\text{}\underline{X}_{\widetilde{\unicode[STIX]{x1D702}}}$
and
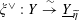 $\unicode[STIX]{x1D709}^{\vee }:Y\stackrel{{\sim}}{\rightarrow }\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
, and representations
$\unicode[STIX]{x1D709}^{\vee }:Y\stackrel{{\sim}}{\rightarrow }\text{}\underline{Y}_{\widetilde{\unicode[STIX]{x1D702}}}$
, and representations
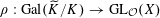 $\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\rightarrow \operatorname{GL}_{{\mathcal{O}}}(X)$
and
$\unicode[STIX]{x1D70C}:\operatorname{Gal}(\widetilde{K}/K)\rightarrow \operatorname{GL}_{{\mathcal{O}}}(X)$
and
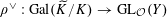 $\unicode[STIX]{x1D70C}^{\vee }:\operatorname{Gal}(\widetilde{K}/K)\rightarrow \operatorname{GL}_{{\mathcal{O}}}(Y)$
defining the descent data for the étale sheaves
$\unicode[STIX]{x1D70C}^{\vee }:\operatorname{Gal}(\widetilde{K}/K)\rightarrow \operatorname{GL}_{{\mathcal{O}}}(Y)$
defining the descent data for the étale sheaves
![]() $\text{}\underline{X}_{\unicode[STIX]{x1D702}}$
and
$\text{}\underline{X}_{\unicode[STIX]{x1D702}}$
and
![]() $\text{}\underline{Y}_{\unicode[STIX]{x1D702}}$
(of left
$\text{}\underline{Y}_{\unicode[STIX]{x1D702}}$
(of left
![]() ${\mathcal{O}}$
-lattices). Then we have an
${\mathcal{O}}$
-lattices). Then we have an
![]() ${\mathcal{O}}$
-equivariant embedding
${\mathcal{O}}$
-equivariant embedding
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:=\unicode[STIX]{x1D709}^{-1}\;\unicode[STIX]{x1D719}_{\widetilde{\unicode[STIX]{x1D702}}}\;\unicode[STIX]{x1D709}^{\vee }:Y{\hookrightarrow}X\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:=\unicode[STIX]{x1D709}^{-1}\;\unicode[STIX]{x1D719}_{\widetilde{\unicode[STIX]{x1D702}}}\;\unicode[STIX]{x1D709}^{\vee }:Y{\hookrightarrow}X\end{eqnarray}$$
with finite cokernel (cf. (5.1)), and the following obvious analogue of Lemma 5.2.
Lemma 7.4. We have
 $$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(\unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D6FE})z)=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z))\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(\unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D6FE})z)=\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})(\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z))\end{eqnarray}$$
for all
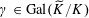 $\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
and
$\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
and
![]() $z\in Y$
.
$z\in Y$
.
Definition 7.5. Given left
![]() ${\mathcal{O}}$
-lattices
${\mathcal{O}}$
-lattices
![]() $M$
and
$M$
and
![]() $M^{\prime }$
, and an abelian group
$M^{\prime }$
, and an abelian group
![]() $M^{\prime \prime }$
(such as
$M^{\prime \prime }$
(such as
![]() $\mathbb{Z}$
or
$\mathbb{Z}$
or
![]() $\widetilde{K}^{\times }$
), we say that a (
$\widetilde{K}^{\times }$
), we say that a (
![]() $\mathbb{Z}$
-)bilinear (or bimultiplicative) pairing
$\mathbb{Z}$
-)bilinear (or bimultiplicative) pairing
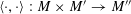 $\langle \cdot ,\cdot \rangle :M\times M^{\prime }\rightarrow M^{\prime \prime }$
is
$\langle \cdot ,\cdot \rangle :M\times M^{\prime }\rightarrow M^{\prime \prime }$
is
![]() ${\mathcal{O}}$
-compatible if
${\mathcal{O}}$
-compatible if
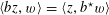 $\langle bz,w\rangle =\langle z,b^{\star }w\rangle$
for all
$\langle bz,w\rangle =\langle z,b^{\star }w\rangle$
for all
![]() $z\in M$
,
$z\in M$
,
![]() $w\in M^{\prime }$
, and
$w\in M^{\prime }$
, and
![]() $b\in {\mathcal{O}}$
.
$b\in {\mathcal{O}}$
.
Remark 7.6. By [Reference Lan14, Lemma 1.1.4.5], the
![]() ${\mathcal{O}}$
-compatible symmetric bilinear pairings
${\mathcal{O}}$
-compatible symmetric bilinear pairings
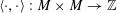 $\langle \cdot ,\cdot \rangle :M\times M\rightarrow \mathbb{Z}$
(as in Definition 7.5, with
$\langle \cdot ,\cdot \rangle :M\times M\rightarrow \mathbb{Z}$
(as in Definition 7.5, with
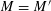 $M=M^{\prime }$
and
$M=M^{\prime }$
and
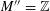 $M^{\prime \prime }=\mathbb{Z}$
) are exactly the traces of the Hermitian pairings
$M^{\prime \prime }=\mathbb{Z}$
) are exactly the traces of the Hermitian pairings
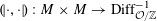 $(\!|\cdot ,\cdot |\!):M\times M\rightarrow \operatorname{Diff}_{{\mathcal{O}}/\mathbb{Z}}^{-1}$
valued in the inverse different
$(\!|\cdot ,\cdot |\!):M\times M\rightarrow \operatorname{Diff}_{{\mathcal{O}}/\mathbb{Z}}^{-1}$
valued in the inverse different
![]() $\operatorname{Diff}_{{\mathcal{O}}/\mathbb{Z}}^{-1}$
(see [Reference Lan14, Definition 1.1.1.8]).
$\operatorname{Diff}_{{\mathcal{O}}/\mathbb{Z}}^{-1}$
(see [Reference Lan14, Definition 1.1.1.8]).
Then we have the following strengthening of Proposition 5.3.
Proposition 7.7. With the setting as above, with the fixed choices of some
![]() $\unicode[STIX]{x1D709}$
,
$\unicode[STIX]{x1D709}$
,
![]() $\unicode[STIX]{x1D709}^{\vee }$
,
$\unicode[STIX]{x1D709}^{\vee }$
,
![]() $\unicode[STIX]{x1D70C}$
, and
$\unicode[STIX]{x1D70C}$
, and
![]() $\unicode[STIX]{x1D70C}^{\vee }$
, the datum of an object
$\unicode[STIX]{x1D70C}^{\vee }$
, the datum of an object
![]() $(G,\unicode[STIX]{x1D706},i)$
of
$(G,\unicode[STIX]{x1D706},i)$
of
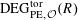 $\operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)$
(as in Definition 7.1) such that
$\operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)$
(as in Definition 7.1) such that
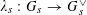 $\unicode[STIX]{x1D706}_{s}:G_{s}\rightarrow G_{s}^{\vee }$
can be identified with
$\unicode[STIX]{x1D706}_{s}:G_{s}\rightarrow G_{s}^{\vee }$
can be identified with
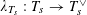 $\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via
$\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via
![]() ${\mathcal{O}}$
-equivariant isomorphisms
${\mathcal{O}}$
-equivariant isomorphisms
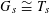 $G_{s}\cong T_{s}$
and
$G_{s}\cong T_{s}$
and
 $G_{s}^{\vee }\cong T_{s}^{\vee }$
over
$G_{s}^{\vee }\cong T_{s}^{\vee }$
over
![]() $s$
) is equivalent to the datum of a bimultiplicative pairing
$s$
) is equivalent to the datum of a bimultiplicative pairing
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:Y\times X\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:Y\times X\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
satisfying the following conditions.
(1) (Galois equivariance)
 $\langle \unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\unicode[STIX]{x1D6FE}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
for all
$\langle \unicode[STIX]{x1D70C}^{\vee }(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\unicode[STIX]{x1D6FE}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
for all
 $z\in Y$
,
$z\in Y$
,
 $w\in X$
, and
$w\in X$
, and
 $\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
.
$\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
.(2) (Symmetry)
 $\langle z,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(w)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle w,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
for all
$\langle z,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(w)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle w,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
for all
 $z,w\in Y$
.
$z,w\in Y$
.(3) (Positivity)
 $\widetilde{\unicode[STIX]{x1D710}}(\langle z,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }})>0$
, for every non-zero
$\widetilde{\unicode[STIX]{x1D710}}(\langle z,\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }})>0$
, for every non-zero
 $z\in Y$
, where
$z\in Y$
, where
 $\widetilde{\unicode[STIX]{x1D710}}:\widetilde{K}^{\times }\rightarrow \mathbb{Z}$
is any non-trivial discrete valuation of
$\widetilde{\unicode[STIX]{x1D710}}:\widetilde{K}^{\times }\rightarrow \mathbb{Z}$
is any non-trivial discrete valuation of
 $\widetilde{K}$
.
$\widetilde{K}$
.(4) (
 ${\mathcal{O}}$
-compatibility)
${\mathcal{O}}$
-compatibility)
 $\langle bz,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle z,b^{\star }w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
for all
$\langle bz,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle z,b^{\star }w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
for all
 $z\in Y$
,
$z\in Y$
,
 $w\in X$
, and
$w\in X$
, and
 $b\in {\mathcal{O}}$
.
$b\in {\mathcal{O}}$
.
Let
![]() ${\mathcal{O}}_{+}$
(respectively
${\mathcal{O}}_{+}$
(respectively
![]() ${\mathcal{O}}_{-}$
) denote the
${\mathcal{O}}_{-}$
) denote the
![]() $\mathbb{Z}$
-submodule of
$\mathbb{Z}$
-submodule of
![]() ${\mathcal{O}}$
consisting of
${\mathcal{O}}$
consisting of
![]() $b\in {\mathcal{O}}$
such that
$b\in {\mathcal{O}}$
such that
![]() $b^{\star }=b$
(respectively
$b^{\star }=b$
(respectively
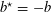 $b^{\star }=-b$
). Note that
$b^{\star }=-b$
). Note that
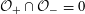 ${\mathcal{O}}_{+}\cap {\mathcal{O}}_{-}=0$
and
${\mathcal{O}}_{+}\cap {\mathcal{O}}_{-}=0$
and
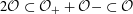 $2{\mathcal{O}}\subset {\mathcal{O}}_{+}+{\mathcal{O}}-\subset {\mathcal{O}}$
, because
$2{\mathcal{O}}\subset {\mathcal{O}}_{+}+{\mathcal{O}}-\subset {\mathcal{O}}$
, because
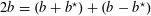 $2b=(b+b^{\star })+(b-b^{\star })$
for all
$2b=(b+b^{\star })+(b-b^{\star })$
for all
![]() $b\in {\mathcal{O}}$
. Let
$b\in {\mathcal{O}}$
. Let
![]() $B_{+}$
(respectively
$B_{+}$
(respectively
![]() $B_{-}$
) denote the
$B_{-}$
) denote the
![]() $\mathbb{Q}$
-subspace of
$\mathbb{Q}$
-subspace of
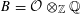 $B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
spanned by
$B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
spanned by
![]() ${\mathcal{O}}_{+}$
(respectively
${\mathcal{O}}_{+}$
(respectively
![]() ${\mathcal{O}}_{-}$
). Then
${\mathcal{O}}_{-}$
). Then
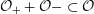 ${\mathcal{O}}_{+}+{\mathcal{O}}-\subset {\mathcal{O}}$
induces
${\mathcal{O}}_{+}+{\mathcal{O}}-\subset {\mathcal{O}}$
induces
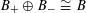 $B_{+}\oplus B_{-}\cong B$
.
$B_{+}\oplus B_{-}\cong B$
.
We have the following rather elaborate analogue of Proposition 5.5.
Proposition 7.9. In the setting of Proposition 7.7, suppose that
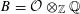 $B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is a division algebra. Suppose that the pairing
$B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is a division algebra. Suppose that the pairing
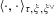 $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
corresponding to
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
corresponding to
![]() $(G,\unicode[STIX]{x1D706})$
satisfies the additional condition that
$(G,\unicode[STIX]{x1D706})$
satisfies the additional condition that
 $$\begin{eqnarray}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1\end{eqnarray}$$
$$\begin{eqnarray}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1\end{eqnarray}$$
for all non-zero
![]() $z\in Y$
and
$z\in Y$
and
![]() $w\in X$
, except when
$w\in X$
, except when
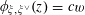 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)=cw$
for some non-zero
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)=cw$
for some non-zero
![]() $c\in B_{-}$
. Then
$c\in B_{-}$
. Then
![]() $G_{\unicode[STIX]{x1D702}}$
and hence
$G_{\unicode[STIX]{x1D702}}$
and hence
![]() $G_{\unicode[STIX]{x1D702}}^{\vee }$
must be absolutely simple, except when
$G_{\unicode[STIX]{x1D702}}^{\vee }$
must be absolutely simple, except when
![]() $B$
belongs to one of the following two special cases (see Remark 7.12 below).
$B$
belongs to one of the following two special cases (see Remark 7.12 below).
(A) The center
 $F$
of the algebra
$F$
of the algebra
 $B$
is a totally real field, and
$B$
is a totally real field, and
 $B\otimes _{F,\unicode[STIX]{x1D70E}}\mathbb{R}$
is isomorphic to the Hamilton quaternion algebra
$B\otimes _{F,\unicode[STIX]{x1D70E}}\mathbb{R}$
is isomorphic to the Hamilton quaternion algebra
 $\mathbb{H}$
over
$\mathbb{H}$
over
 $\mathbb{R}$
for every field homomorphism
$\mathbb{R}$
for every field homomorphism
 $\unicode[STIX]{x1D70E}:F\rightarrow \mathbb{R}$
, with the positive involution
$\unicode[STIX]{x1D70E}:F\rightarrow \mathbb{R}$
, with the positive involution
 $\star$
of
$\star$
of
 $B$
induced by the canonical positive involution
$B$
induced by the canonical positive involution
 $x\mapsto \operatorname{Tr}_{\mathbb{H}/\mathbb{R}}(x)-x$
on
$x\mapsto \operatorname{Tr}_{\mathbb{H}/\mathbb{R}}(x)-x$
on
 $\mathbb{H}$
. (This is exactly the third case in [Reference Lan14, Proposition 1.2.1.13].) Also,
$\mathbb{H}$
. (This is exactly the third case in [Reference Lan14, Proposition 1.2.1.13].) Also,
 $Y\otimes _{\mathbb{Z}}\mathbb{Q}\cong B$
as
$Y\otimes _{\mathbb{Z}}\mathbb{Q}\cong B$
as
 $B$
-modules.
$B$
-modules.(B) The center
 $F$
of the algebra
$F$
of the algebra
 $B$
is a CM field (i.e. is a totally imaginary extension of a totally real field
$B$
is a CM field (i.e. is a totally imaginary extension of a totally real field
 $F_{+}$
), and
$F_{+}$
), and
 $B=F$
. (This is a very special case of the fourth case in [Reference Lan14, Proposition 1.2.1.13].) Also,
$B=F$
. (This is a very special case of the fourth case in [Reference Lan14, Proposition 1.2.1.13].) Also,
 $Y\otimes _{\mathbb{Z}}\mathbb{Q}\cong B$
as
$Y\otimes _{\mathbb{Z}}\mathbb{Q}\cong B$
as
 $B$
-modules.
$B$
-modules.
Remark 7.11. The assumption that
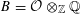 $B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is a division algebra is natural for our purpose, because the existence of any non-trivial idempotent in
$B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is a division algebra is natural for our purpose, because the existence of any non-trivial idempotent in
![]() $B$
will force
$B$
will force
![]() $G_{\unicode[STIX]{x1D702}}$
to be isogenous to a non-trivial product of abelian varieties of smaller dimensions.
$G_{\unicode[STIX]{x1D702}}$
to be isogenous to a non-trivial product of abelian varieties of smaller dimensions.
Remark 7.12. The two exceptional cases (A) and (B) in Proposition 7.9 (and therefore also in Theorems 7.20, 7.22, and 7.24 below) are unavoidable for the following reasons. Suppose
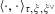 $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
is any pairing, with associated
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
is any pairing, with associated
![]() $G$
over
$G$
over
![]() $S$
, as in Proposition 7.7. For simplicity, let us identify
$S$
, as in Proposition 7.7. For simplicity, let us identify
![]() $Y$
with its image
$Y$
with its image
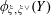 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(Y)$
in
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(Y)$
in
![]() $X$
, and suppress
$X$
, and suppress
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
from the notation. In the case (A), there exist
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
from the notation. In the case (A), there exist
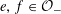 $e,f\in {\mathcal{O}}_{-}$
such that
$e,f\in {\mathcal{O}}_{-}$
such that
 $B=B^{\prime }\oplus fB^{\prime }$
as modules of the (commutative) CM field
$B=B^{\prime }\oplus fB^{\prime }$
as modules of the (commutative) CM field
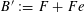 $B^{\prime }:=F+Fe$
, by letting
$B^{\prime }:=F+Fe$
, by letting
![]() $B^{\prime }$
act on
$B^{\prime }$
act on
![]() $B$
by right multiplication. Since
$B$
by right multiplication. Since
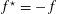 $f^{\star }=-f$
, for any
$f^{\star }=-f$
, for any
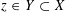 $z\in Y\subset X$
, we have
$z\in Y\subset X$
, we have
 $$\begin{eqnarray}\displaystyle \langle az,4fbz\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }} & = & \displaystyle \langle az,2fbz\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\cdot \langle -2faz,bz\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\nonumber\\ \displaystyle & = & \displaystyle \langle z,2(a^{\star }fb-b^{\star }fa)z\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\nonumber\\ \displaystyle & = & \displaystyle \langle z,(a^{\star }fb-b^{\star }fa)z\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\cdot \langle (b^{\star }fa-a^{\star }fb)z,z\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\nonumber\\ \displaystyle & = & \displaystyle 1,\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \langle az,4fbz\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }} & = & \displaystyle \langle az,2fbz\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\cdot \langle -2faz,bz\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\nonumber\\ \displaystyle & = & \displaystyle \langle z,2(a^{\star }fb-b^{\star }fa)z\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\nonumber\\ \displaystyle & = & \displaystyle \langle z,(a^{\star }fb-b^{\star }fa)z\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\cdot \langle (b^{\star }fa-a^{\star }fb)z,z\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\nonumber\\ \displaystyle & = & \displaystyle 1,\nonumber\end{eqnarray}$$
for all
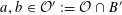 $a,b\in {\mathcal{O}}^{\prime }:={\mathcal{O}}\cap B^{\prime }$
. Similarly, in the case (B), there exists
$a,b\in {\mathcal{O}}^{\prime }:={\mathcal{O}}\cap B^{\prime }$
. Similarly, in the case (B), there exists
![]() $e\in {\mathcal{O}}_{-}$
such that
$e\in {\mathcal{O}}_{-}$
such that
 $B=F=B^{\prime }\oplus B^{\prime }e$
as modules of the (commutative) totally real field
$B=F=B^{\prime }\oplus B^{\prime }e$
as modules of the (commutative) totally real field
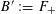 $B^{\prime }:=F_{+}$
. Since
$B^{\prime }:=F_{+}$
. Since
![]() $e^{\star }=-e$
, and since
$e^{\star }=-e$
, and since
![]() $B=F$
is commutative, for any
$B=F$
is commutative, for any
 $z\in Y\subset X$
, we have
$z\in Y\subset X$
, we have
 $$\begin{eqnarray}\langle az,2bez\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle abz,ez\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\cdot \langle -ez,abz\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=1,\end{eqnarray}$$
$$\begin{eqnarray}\langle az,2bez\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=\langle abz,ez\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\cdot \langle -ez,abz\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}=1,\end{eqnarray}$$
for all
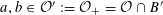 $a,b\in {\mathcal{O}}^{\prime }:={\mathcal{O}}_{+}={\mathcal{O}}\cap B^{\prime }$
. Hence, in both cases, up to replacing
$a,b\in {\mathcal{O}}^{\prime }:={\mathcal{O}}_{+}={\mathcal{O}}\cap B^{\prime }$
. Hence, in both cases, up to replacing
![]() $Y$
and
$Y$
and
![]() $X$
with some sublattices of finite indices, the pairing
$X$
with some sublattices of finite indices, the pairing
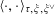 $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
decomposes into an orthogonal direct sum of two pairings that are symmetric, positive, and compatible with the order
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
decomposes into an orthogonal direct sum of two pairings that are symmetric, positive, and compatible with the order
![]() ${\mathcal{O}}^{\prime }$
in
${\mathcal{O}}^{\prime }$
in
![]() $B^{\prime }$
(but not necessarily Galois equivariant) as in Proposition 7.7. Therefore, the base change
$B^{\prime }$
(but not necessarily Galois equivariant) as in Proposition 7.7. Therefore, the base change
![]() $G_{\bar{\unicode[STIX]{x1D702}}}$
of
$G_{\bar{\unicode[STIX]{x1D702}}}$
of
![]() $G_{\unicode[STIX]{x1D702}}$
to any geometric point
$G_{\unicode[STIX]{x1D702}}$
to any geometric point
![]() $\bar{\unicode[STIX]{x1D702}}\rightarrow S$
above
$\bar{\unicode[STIX]{x1D702}}\rightarrow S$
above
![]() $\unicode[STIX]{x1D702}\rightarrow S$
is isogenous to a product of two abelian varieties over
$\unicode[STIX]{x1D702}\rightarrow S$
is isogenous to a product of two abelian varieties over
![]() $\bar{\unicode[STIX]{x1D702}}$
with endomorphisms by
$\bar{\unicode[STIX]{x1D702}}$
with endomorphisms by
![]() ${\mathcal{O}}^{\prime }$
, both of which are simple by applying Proposition 7.9 with
${\mathcal{O}}^{\prime }$
, both of which are simple by applying Proposition 7.9 with
![]() ${\mathcal{O}}$
replaced with
${\mathcal{O}}$
replaced with
![]() ${\mathcal{O}}^{\prime }$
. (Moreover, these two simple abelian varieties are isogenous to each other by the same argument as in the second paragraph of the proof of Proposition 7.9 below.) In particular,
${\mathcal{O}}^{\prime }$
. (Moreover, these two simple abelian varieties are isogenous to each other by the same argument as in the second paragraph of the proof of Proposition 7.9 below.) In particular,
![]() $G_{\unicode[STIX]{x1D702}}$
can never be absolutely simple in these two exceptional cases.
$G_{\unicode[STIX]{x1D702}}$
can never be absolutely simple in these two exceptional cases.
Proof of Proposition 7.9.
Without loss of generality, we may and we shall assume that
![]() $Y\neq 0$
, so that
$Y\neq 0$
, so that
![]() $G_{\unicode[STIX]{x1D702}}$
is a non-trivial abelian variety over
$G_{\unicode[STIX]{x1D702}}$
is a non-trivial abelian variety over
![]() $\unicode[STIX]{x1D702}$
.
$\unicode[STIX]{x1D702}$
.
The condition (7.10) implies the weaker condition that, for any given non-zero
![]() $z\in Y$
and
$z\in Y$
and
![]() $w\in X$
, there exists some
$w\in X$
, there exists some
![]() $b\in {\mathcal{O}}$
such that
$b\in {\mathcal{O}}$
such that
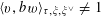 $\langle v,bw\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
. By the same argument as in the proof of Proposition 5.5, this implies that
$\langle v,bw\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
. By the same argument as in the proof of Proposition 5.5, this implies that
![]() $G_{\unicode[STIX]{x1D702}}$
and hence
$G_{\unicode[STIX]{x1D702}}$
and hence
![]() $G_{\unicode[STIX]{x1D702}}^{\vee }$
are absolutely simple in the category of abelian varieties with endomorphisms by
$G_{\unicode[STIX]{x1D702}}^{\vee }$
are absolutely simple in the category of abelian varieties with endomorphisms by
![]() ${\mathcal{O}}$
, in the sense that their base changes
${\mathcal{O}}$
, in the sense that their base changes
![]() $G_{\bar{\unicode[STIX]{x1D702}}}$
and
$G_{\bar{\unicode[STIX]{x1D702}}}$
and
![]() $G_{\bar{\unicode[STIX]{x1D702}}}^{\vee }$
to any geometric point
$G_{\bar{\unicode[STIX]{x1D702}}}^{\vee }$
to any geometric point
![]() $\bar{\unicode[STIX]{x1D702}}\rightarrow S$
above
$\bar{\unicode[STIX]{x1D702}}\rightarrow S$
above
![]() $\unicode[STIX]{x1D702}\rightarrow S$
are not isogenous to non-trivial products of abelian varieties of smaller dimensions with endomorphisms by
$\unicode[STIX]{x1D702}\rightarrow S$
are not isogenous to non-trivial products of abelian varieties of smaller dimensions with endomorphisms by
![]() ${\mathcal{O}}$
. Moreover, if
${\mathcal{O}}$
. Moreover, if
![]() $G_{\bar{\unicode[STIX]{x1D702}}}$
is isogenous to a product
$G_{\bar{\unicode[STIX]{x1D702}}}$
is isogenous to a product
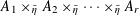 $A_{1}\times _{\bar{\unicode[STIX]{x1D702}}}A_{2}\times _{\bar{\unicode[STIX]{x1D702}}}\cdots \times _{\bar{\unicode[STIX]{x1D702}}}A_{r}$
of simple abelian subvarieties over
$A_{1}\times _{\bar{\unicode[STIX]{x1D702}}}A_{2}\times _{\bar{\unicode[STIX]{x1D702}}}\cdots \times _{\bar{\unicode[STIX]{x1D702}}}A_{r}$
of simple abelian subvarieties over
![]() $\bar{\unicode[STIX]{x1D702}}$
, then the actions of elements of
$\bar{\unicode[STIX]{x1D702}}$
, then the actions of elements of
![]() ${\mathcal{O}}$
on
${\mathcal{O}}$
on
![]() $G_{\bar{\unicode[STIX]{x1D702}}}$
induce quasi-isogenies between all possible pairs
$G_{\bar{\unicode[STIX]{x1D702}}}$
induce quasi-isogenies between all possible pairs
![]() $A_{i}$
and
$A_{i}$
and
![]() $A_{j}$
, with
$A_{j}$
, with
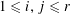 $1\leqslant i,j\leqslant r$
, because otherwise
$1\leqslant i,j\leqslant r$
, because otherwise
![]() $G_{\bar{\unicode[STIX]{x1D702}}}$
cannot be absolutely simple in the category of abelian varieties with endomorphisms by
$G_{\bar{\unicode[STIX]{x1D702}}}$
cannot be absolutely simple in the category of abelian varieties with endomorphisms by
![]() ${\mathcal{O}}$
. Hence, we may assume that
${\mathcal{O}}$
. Hence, we may assume that
![]() $G_{\bar{\unicode[STIX]{x1D702}}}$
is isogenous to
$G_{\bar{\unicode[STIX]{x1D702}}}$
is isogenous to
![]() $A^{r}$
for some (non-trivial) simple abelian variety
$A^{r}$
for some (non-trivial) simple abelian variety
![]() $A$
over
$A$
over
![]() $\bar{\unicode[STIX]{x1D702}}$
, for some integer
$\bar{\unicode[STIX]{x1D702}}$
, for some integer
![]() $r\geqslant 1$
. Note that
$r\geqslant 1$
. Note that
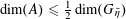 $\dim (A)\leqslant \frac{1}{2}\dim (G_{\bar{\unicode[STIX]{x1D702}}})$
when
$\dim (A)\leqslant \frac{1}{2}\dim (G_{\bar{\unicode[STIX]{x1D702}}})$
when
![]() $r\geqslant 2$
.
$r\geqslant 2$
.
For simplicity, let us identify
![]() $Y$
with its image
$Y$
with its image
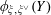 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(Y)$
in
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(Y)$
in
![]() $X$
, and suppress
$X$
, and suppress
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
from the notation. Suppose
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
from the notation. Suppose
 $e_{1},e_{2},\ldots ,e_{n}$
are elements of
$e_{1},e_{2},\ldots ,e_{n}$
are elements of
![]() $Y$
such that the assignment
$Y$
such that the assignment
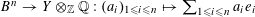 $B^{n}\rightarrow Y\otimes _{\mathbb{Z}}\mathbb{Q}:(a_{i})_{1\leqslant i\leqslant n}\mapsto \sum _{1\leqslant i\leqslant n}a_{i}e_{i}$
induces an isomorphism of left
$B^{n}\rightarrow Y\otimes _{\mathbb{Z}}\mathbb{Q}:(a_{i})_{1\leqslant i\leqslant n}\mapsto \sum _{1\leqslant i\leqslant n}a_{i}e_{i}$
induces an isomorphism of left
![]() $B$
-modules (which is possible because
$B$
-modules (which is possible because
![]() $B$
is a division algebra, whose simple modules are all isomorphic to
$B$
is a division algebra, whose simple modules are all isomorphic to
![]() $B$
itself; see [Reference Lan14, Lemma 1.1.2.4]).
$B$
itself; see [Reference Lan14, Lemma 1.1.2.4]).
Suppose
![]() $n\geqslant 2$
. Then we have
$n\geqslant 2$
. Then we have
 $\langle e_{1},be_{j}\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
for all
$\langle e_{1},be_{j}\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
for all
![]() $j>1$
and all
$j>1$
and all
![]() $b\in {\mathcal{O}}$
. Note that the dimension of the
$b\in {\mathcal{O}}$
. Note that the dimension of the
![]() $\mathbb{Q}$
-span of
$\mathbb{Q}$
-span of
![]() $e_{1}$
and all the
$e_{1}$
and all the
![]() $be_{j}$
for all
$be_{j}$
for all
![]() $j>1$
and all
$j>1$
and all
![]() $b\in {\mathcal{O}}$
is greater than
$b\in {\mathcal{O}}$
is greater than
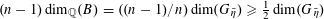 $(n-1)\dim _{\mathbb{Q}}(B)=((n-1)/n)\dim (G_{\bar{\unicode[STIX]{x1D702}}})\geqslant \frac{1}{2}\dim (G_{\bar{\unicode[STIX]{x1D702}}})$
. This shows that
$(n-1)\dim _{\mathbb{Q}}(B)=((n-1)/n)\dim (G_{\bar{\unicode[STIX]{x1D702}}})\geqslant \frac{1}{2}\dim (G_{\bar{\unicode[STIX]{x1D702}}})$
. This shows that
 $\dim (A)>\frac{1}{2}\dim (G_{\bar{\unicode[STIX]{x1D702}}})$
, so that
$\dim (A)>\frac{1}{2}\dim (G_{\bar{\unicode[STIX]{x1D702}}})$
, so that
![]() $r=1$
. That is,
$r=1$
. That is,
![]() $G_{\bar{\unicode[STIX]{x1D702}}}$
is simple whenever
$G_{\bar{\unicode[STIX]{x1D702}}}$
is simple whenever
![]() $n\geqslant 2$
.
$n\geqslant 2$
.
Suppose
![]() $n=1$
, so that
$n=1$
, so that
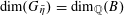 $\dim (G_{\bar{\unicode[STIX]{x1D702}}})=\dim _{\mathbb{Q}}(B)$
. Let
$\dim (G_{\bar{\unicode[STIX]{x1D702}}})=\dim _{\mathbb{Q}}(B)$
. Let
![]() $F$
denote the center of
$F$
denote the center of
![]() $B$
. We have four cases of the division algebra
$B$
. We have four cases of the division algebra
![]() $B$
with the positive involution
$B$
with the positive involution
![]() $\star$
, as in [Reference Mumford17, §21] or [Reference Lan14, Proposition 1.2.1.13].
$\star$
, as in [Reference Mumford17, §21] or [Reference Lan14, Proposition 1.2.1.13].
(I) The center
 $F$
is a totally real field, and
$F$
is a totally real field, and
 $B=F$
, with the trivial involution
$B=F$
, with the trivial involution
 $\star$
. In this case, we have
$\star$
. In this case, we have
 $B_{-}=0$
, and
$B_{-}=0$
, and
 $G_{\bar{\unicode[STIX]{x1D702}}}$
is simple by Proposition 5.5, because the condition (7.10) here is identical to the corresponding condition (5.6) there.
$G_{\bar{\unicode[STIX]{x1D702}}}$
is simple by Proposition 5.5, because the condition (7.10) here is identical to the corresponding condition (5.6) there.(II) The center
 $F$
is a totally real field, and
$F$
is a totally real field, and
 $B\otimes _{F,\unicode[STIX]{x1D70E}}\mathbb{R}$
is isomorphic to
$B\otimes _{F,\unicode[STIX]{x1D70E}}\mathbb{R}$
is isomorphic to
 $\operatorname{M}_{2}(\mathbb{R})$
over
$\operatorname{M}_{2}(\mathbb{R})$
over
 $\mathbb{R}$
for every field homomorphism
$\mathbb{R}$
for every field homomorphism
 $\unicode[STIX]{x1D70E}:F\rightarrow \mathbb{R}$
, with the positive involution
$\unicode[STIX]{x1D70E}:F\rightarrow \mathbb{R}$
, with the positive involution
 $\star$
of
$\star$
of
 $B$
induced by some conjugation of the canonical positive involution
$B$
induced by some conjugation of the canonical positive involution
 $x\mapsto ^{t}x$
of
$x\mapsto ^{t}x$
of
 $\operatorname{M}_{2}(\mathbb{R})$
. In this case, since
$\operatorname{M}_{2}(\mathbb{R})$
. In this case, since
 $\langle e_{1},be_{1}\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
for all
$\langle e_{1},be_{1}\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
for all
 $b\in {\mathcal{O}}_{+}$
, and since
$b\in {\mathcal{O}}_{+}$
, and since
 $\dim _{\mathbb{Q}}(B_{+})=\frac{3}{4}\dim _{\mathbb{Q}}(B)>\frac{1}{2}\dim _{\mathbb{Q}}(B)=\frac{1}{2}\dim (G_{\bar{\unicode[STIX]{x1D702}}})$
, we can conclude as before that
$\dim _{\mathbb{Q}}(B_{+})=\frac{3}{4}\dim _{\mathbb{Q}}(B)>\frac{1}{2}\dim _{\mathbb{Q}}(B)=\frac{1}{2}\dim (G_{\bar{\unicode[STIX]{x1D702}}})$
, we can conclude as before that
 $r=1$
, so that
$r=1$
, so that
 $G_{\bar{\unicode[STIX]{x1D702}}}$
is simple.
$G_{\bar{\unicode[STIX]{x1D702}}}$
is simple.(III) The center
 $F$
is a totally real field, and
$F$
is a totally real field, and
 $B\otimes _{F,\unicode[STIX]{x1D70E}}\mathbb{R}$
is isomorphic to the Hamilton quaternion algebra
$B\otimes _{F,\unicode[STIX]{x1D70E}}\mathbb{R}$
is isomorphic to the Hamilton quaternion algebra
 $\mathbb{H}$
over
$\mathbb{H}$
over
 $\mathbb{R}$
for every field homomorphism
$\mathbb{R}$
for every field homomorphism
 $\unicode[STIX]{x1D70E}:F\rightarrow \mathbb{R}$
. This is exactly the exceptional case (A) in the proposition.
$\unicode[STIX]{x1D70E}:F\rightarrow \mathbb{R}$
. This is exactly the exceptional case (A) in the proposition.(IV) The center
 $F$
is a totally imaginary extension of a totally real field
$F$
is a totally imaginary extension of a totally real field
 $F_{+}$
, with the restriction of the involution
$F_{+}$
, with the restriction of the involution
 $\star$
to
$\star$
to
 $F$
given by the complex conjugation over
$F$
given by the complex conjugation over
 $F_{+}$
. (We shall ignore the additional conditions satisfied by
$F_{+}$
. (We shall ignore the additional conditions satisfied by
 $B$
.) In this case, since
$B$
.) In this case, since
 $\langle e_{1},be_{1}\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
for all
$\langle e_{1},be_{1}\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
for all
 $b\in {\mathcal{O}}_{+}$
, and since
$b\in {\mathcal{O}}_{+}$
, and since
 $\dim _{\mathbb{Q}}(B_{+})=\frac{1}{2}\dim _{\mathbb{Q}}(B)$
, we have
$\dim _{\mathbb{Q}}(B_{+})=\frac{1}{2}\dim _{\mathbb{Q}}(B)$
, we have
 $r\leqslant 2$
. If
$r\leqslant 2$
. If
 $r=1$
, then
$r=1$
, then
 $G_{\bar{\unicode[STIX]{x1D702}}}$
is simple, as desired.
$G_{\bar{\unicode[STIX]{x1D702}}}$
is simple, as desired.Otherwise, we necessarily have
 $r=2$
. Let
$r=2$
. Let
 $D:=\operatorname{End}_{\bar{\unicode[STIX]{x1D702}}}(A)\otimes _{\mathbb{Z}}\mathbb{Q}$
, which is a division algebra with a positive involution, because
$D:=\operatorname{End}_{\bar{\unicode[STIX]{x1D702}}}(A)\otimes _{\mathbb{Z}}\mathbb{Q}$
, which is a division algebra with a positive involution, because
 $A$
is a simple abelian variety. (See, for example, [Reference Mumford17, §§20–21].) Then we have an injective homomorphism
$A$
is a simple abelian variety. (See, for example, [Reference Mumford17, §§20–21].) Then we have an injective homomorphism
 $B{\hookrightarrow}\operatorname{M}_{2}(D)$
of algebras over
$B{\hookrightarrow}\operatorname{M}_{2}(D)$
of algebras over
 $\mathbb{Q}$
, which cannot be an isomorphism because
$\mathbb{Q}$
, which cannot be an isomorphism because
 $B$
is a division algebra but
$B$
is a division algebra but
 $\operatorname{M}_{2}(D)$
is not. Since the action of the order
$\operatorname{M}_{2}(D)$
is not. Since the action of the order
 $\operatorname{End}_{\bar{\unicode[STIX]{x1D702}}}(A)$
in
$\operatorname{End}_{\bar{\unicode[STIX]{x1D702}}}(A)$
in
 $D$
induces an action of the same order on the character group of the torus degeneration of
$D$
induces an action of the same order on the character group of the torus degeneration of
 $A$
, we have an action of
$A$
, we have an action of
 $D$
on
$D$
on
 $B$
stabilizing the
$B$
stabilizing the
 $\mathbb{Q}$
-subspaces
$\mathbb{Q}$
-subspaces
 $B_{+}$
and
$B_{+}$
and
 $B_{-}$
of the same dimension, so that
$B_{-}$
of the same dimension, so that
 $B\cong B_{+}\oplus B_{-}$
and
$B\cong B_{+}\oplus B_{-}$
and
 $B_{+}\cong D^{r^{\prime }}\cong B_{-}$
as
$B_{+}\cong D^{r^{\prime }}\cong B_{-}$
as
 $D$
-modules, for some integer
$D$
-modules, for some integer
 $r^{\prime }\geqslant 1$
. Then we have
$r^{\prime }\geqslant 1$
. Then we have
 $2r^{\prime }\dim _{\mathbb{Q}}(D)\leqslant \dim _{\mathbb{Q}}(B)<4\dim _{\mathbb{Q}}(D)$
, forcing
$2r^{\prime }\dim _{\mathbb{Q}}(D)\leqslant \dim _{\mathbb{Q}}(B)<4\dim _{\mathbb{Q}}(D)$
, forcing
 $r^{\prime }=1$
.
$r^{\prime }=1$
.Let
 $E$
denote the center of
$E$
denote the center of
 $D$
, which is a field and is also the center of
$D$
, which is a field and is also the center of
 $\operatorname{M}_{2}(D)$
. Then
$\operatorname{M}_{2}(D)$
. Then
 $E_{0}:=B\cap E$
is a subfield of the center
$E_{0}:=B\cap E$
is a subfield of the center
 $F$
of
$F$
of
 $B$
, because
$B$
, because
 $E$
commutes with all elements of
$E$
commutes with all elements of
 $B$
. If
$B$
. If
 $E_{0}=E$
, then
$E_{0}=E$
, then
 $E$
is a subfield of
$E$
is a subfield of
 $F$
. Otherwise, the
$F$
. Otherwise, the
 $E$
-span
$E$
-span
 $B^{\prime }$
of the image of
$B^{\prime }$
of the image of
 $B$
in
$B$
in
 $\operatorname{M}_{2}(D)$
form an
$\operatorname{M}_{2}(D)$
form an
 $E$
-subalgebra of
$E$
-subalgebra of
 $\operatorname{M}_{2}(D)$
such that
$\operatorname{M}_{2}(D)$
such that
 $\dim _{\mathbb{Q}}(B^{\prime })\geqslant 2\dim _{\mathbb{Q}}(B)=4\dim _{\mathbb{Q}}(D)$
, which must be the whole of
$\dim _{\mathbb{Q}}(B^{\prime })\geqslant 2\dim _{\mathbb{Q}}(B)=4\dim _{\mathbb{Q}}(D)$
, which must be the whole of
 $\operatorname{M}_{2}(D)$
. Therefore,
$\operatorname{M}_{2}(D)$
. Therefore,
 $B\otimes _{E_{0}}E\cong \operatorname{M}_{2}(D)$
is simple, which implies that
$B\otimes _{E_{0}}E\cong \operatorname{M}_{2}(D)$
is simple, which implies that
 $F=E_{0}$
. In particular, we have either
$F=E_{0}$
. In particular, we have either
 $E\subset F$
or
$E\subset F$
or
 $F\subset E$
.
$F\subset E$
.Since
 $E$
is the center of an endomorphism algebra of a simple abelian variety, it is either a totally real field or a CM field. If
$E$
is the center of an endomorphism algebra of a simple abelian variety, it is either a totally real field or a CM field. If
 $E$
is a CM field, then there exists some non-zero
$E$
is a CM field, then there exists some non-zero
 $c\in E_{0}=E\cap F$
such that
$c\in E_{0}=E\cap F$
such that
 $c^{\star }=-c$
, so that
$c^{\star }=-c$
, so that
 $cB_{+}=B_{-}$
, contradicting the assumption that
$cB_{+}=B_{-}$
, contradicting the assumption that
 $D$
stabilizes
$D$
stabilizes
 $B_{+}$
. Hence,
$B_{+}$
. Hence,
 $E$
is necessarily a totally real subfield, in which case
$E$
is necessarily a totally real subfield, in which case
 $[D:E]$
is either
$[D:E]$
is either
 $4$
or
$4$
or
 $1$
, and
$1$
, and
 $E\subset F$
(because
$E\subset F$
(because
 $F\subset E$
cannot happen, since
$F\subset E$
cannot happen, since
 $F$
is a CM field).
$F$
is a CM field).Let
 $C$
denote the centralizer of
$C$
denote the centralizer of
 $B$
in
$B$
in
 $\operatorname{M}_{2}(D)$
. By [Reference Jacobson10, Ch. 5, §11, Theorem 19], we have
$\operatorname{M}_{2}(D)$
. By [Reference Jacobson10, Ch. 5, §11, Theorem 19], we have
 $[B:E][C:E]=[\operatorname{M}_{2}(D):E]=4[D:E]$
.
$[B:E][C:E]=[\operatorname{M}_{2}(D):E]=4[D:E]$
.If
 $[D:E]=4$
, then
$[D:E]=4$
, then
 $[F:E]^{2}|[B:E][C:E]=16$
, and so
$[F:E]^{2}|[B:E][C:E]=16$
, and so
 $[F:E]$
is either
$[F:E]$
is either
 $4$
or
$4$
or
 $2$
, and
$2$
, and
 $[B:F]$
is either
$[B:F]$
is either
 $1$
or
$1$
or
 $4$
. If
$4$
. If
 $[B:F]=1$
, then the torus degeneration of
$[B:F]=1$
, then the torus degeneration of
 $A$
is of dimension
$A$
is of dimension
 $\frac{1}{2}\dim _{\mathbb{Q}}(B)=\frac{1}{2}\dim _{\mathbb{Q}}(F)\leqslant 2\dim _{\mathbb{Q}}(E)$
, which cannot admit an action of the quaternion algebra
$\frac{1}{2}\dim _{\mathbb{Q}}(B)=\frac{1}{2}\dim _{\mathbb{Q}}(F)\leqslant 2\dim _{\mathbb{Q}}(E)$
, which cannot admit an action of the quaternion algebra
 $D$
over
$D$
over
 $E$
. If
$E$
. If
 $[B:F]=4$
, then
$[B:F]=4$
, then
 $[F:E]=2$
and
$[F:E]=2$
and
 $C=F$
, forcing
$C=F$
, forcing
 $F_{+}=E$
. Consider any
$F_{+}=E$
. Consider any
 $f\in F$
such that
$f\in F$
such that
 $f^{\star }=-f$
, so that
$f^{\star }=-f$
, so that
 $F=E[f]=E+Ef$
. Then
$F=E[f]=E+Ef$
. Then
 $B_{-}=B_{+}\cdot f$
and
$B_{-}=B_{+}\cdot f$
and
 $B_{+}=B_{-}\cdot f$
, and the left actions of
$B_{+}=B_{-}\cdot f$
, and the left actions of
 $D$
and
$D$
and
 $F$
on
$F$
on
 $B$
commute with each other because the left action of
$B$
commute with each other because the left action of
 $f$
on
$f$
on
 $B$
can be equivalently given by the right multiplication by
$B$
can be equivalently given by the right multiplication by
 $f$
, and because
$f$
, and because
 $f^{2}\in F_{+}=E$
commutes with
$f^{2}\in F_{+}=E$
commutes with
 $D$
. Then
$D$
. Then
 $D\otimes _{E}F$
can be canonically identified with an
$D\otimes _{E}F$
can be canonically identified with an
 $E$
-subalgebra of
$E$
-subalgebra of
 $\operatorname{M}_{2}(D)$
, and the centralizers of
$\operatorname{M}_{2}(D)$
, and the centralizers of
 $E\subset F\subset \operatorname{M}_{2}(E)$
are
$E\subset F\subset \operatorname{M}_{2}(E)$
are
 $\operatorname{M}_{2}(D)\supset D\otimes _{E}F\supset D$
, respectively. Consequently,
$\operatorname{M}_{2}(D)\supset D\otimes _{E}F\supset D$
, respectively. Consequently,
 $B=D\otimes _{E}F$
as
$B=D\otimes _{E}F$
as
 $E$
-subalgebras of
$E$
-subalgebras of
 $\operatorname{M}_{2}(D)$
, because the centralizer of
$\operatorname{M}_{2}(D)$
, because the centralizer of
 $C=F$
is
$C=F$
is
 $B$
, by [Reference Jacobson10, Ch. 5, §11, Theorem 19] again. Since the positive involution
$B$
, by [Reference Jacobson10, Ch. 5, §11, Theorem 19] again. Since the positive involution
 $\star$
of
$\star$
of
 $B$
restricts to a positive involution on
$B$
restricts to a positive involution on
 $D$
, and since this restriction cannot be trivial because
$D$
, and since this restriction cannot be trivial because
 $D$
is a quaternion algebra over
$D$
is a quaternion algebra over
 $E$
(and because of Albert’s classification), there exists some non-zero
$E$
(and because of Albert’s classification), there exists some non-zero
 $d\in D\cap B_{-}$
. But then
$d\in D\cap B_{-}$
. But then
 $d^{-1}$
exists in
$d^{-1}$
exists in
 $D$
, and the left multiplication by
$D$
, and the left multiplication by
 $d^{-1}\in D$
maps
$d^{-1}\in D$
maps
 $d\in B_{-}$
to the non-zero
$d\in B_{-}$
to the non-zero
 $1\in B_{+}$
, contradicting the assumption that
$1\in B_{+}$
, contradicting the assumption that
 $D$
stabilizes
$D$
stabilizes
 $B_{-}$
.
$B_{-}$
.Finally, if
 $[D:E]=1$
, then
$[D:E]=1$
, then
 $[F:E]^{2}|[B:E][C:E]=4$
, and so
$[F:E]^{2}|[B:E][C:E]=4$
, and so
 $[F:E]=2$
and
$[F:E]=2$
and
 $B=F=C$
. This is exactly the exceptional case (B) in the proposition.
$B=F=C$
. This is exactly the exceptional case (B) in the proposition.
Thus, we have shown that
![]() $G_{\unicode[STIX]{x1D702}}$
and, hence,
$G_{\unicode[STIX]{x1D702}}$
and, hence,
![]() $G_{\unicode[STIX]{x1D702}}^{\vee }$
are absolutely simple except in the two cases (A) and (B) in the proposition, as desired.◻
$G_{\unicode[STIX]{x1D702}}^{\vee }$
are absolutely simple except in the two cases (A) and (B) in the proposition, as desired.◻
Hence, the key point is to establish the following analogue of Proposition 5.14.
Proposition 7.13. Suppose that
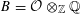 $B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is a division algebra. Then there exists a bimultiplicative pairing
$B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is a division algebra. Then there exists a bimultiplicative pairing
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:Y\times X\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:Y\times X\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
as in (7.8) satisfying all the conditions in Propositions 7.7 and 7.9.
Proof. The idea is similar to that in the proof of Proposition 5.14, but the implementation here is, perhaps unavoidably, more tedious. Let
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{0}:X\times X\rightarrow \mathbb{Z}\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{0}:X\times X\rightarrow \mathbb{Z}\end{eqnarray}$$
be any positive definite
![]() ${\mathcal{O}}$
-compatible (symmetric) bilinear pairing (which exists by the same argument as in the proof of, for example, [Reference Lan13, Lemma 2.5]).
${\mathcal{O}}$
-compatible (symmetric) bilinear pairing (which exists by the same argument as in the proof of, for example, [Reference Lan13, Lemma 2.5]).
Suppose
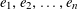 $e_{1},e_{2},\ldots ,e_{n}$
are elements of
$e_{1},e_{2},\ldots ,e_{n}$
are elements of
![]() $X\otimes _{\mathbb{Z}}\mathbb{Q}$
such that the assignment
$X\otimes _{\mathbb{Z}}\mathbb{Q}$
such that the assignment
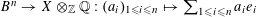 $B^{n}\rightarrow X\otimes _{\mathbb{Z}}\mathbb{Q}:(a_{i})_{1\leqslant i\leqslant n}\mapsto \sum _{1\leqslant i\leqslant n}a_{i}e_{i}$
induces an isomorphism of left
$B^{n}\rightarrow X\otimes _{\mathbb{Z}}\mathbb{Q}:(a_{i})_{1\leqslant i\leqslant n}\mapsto \sum _{1\leqslant i\leqslant n}a_{i}e_{i}$
induces an isomorphism of left
![]() $B$
-modules (which, again, is possible because
$B$
-modules (which, again, is possible because
![]() $B$
is a division algebra, whose simple modules are all isomorphic to
$B$
is a division algebra, whose simple modules are all isomorphic to
![]() $B$
itself; see [Reference Lan14, Lemma 1.1.2.4]), and such that
$B$
itself; see [Reference Lan14, Lemma 1.1.2.4]), and such that
![]() $X$
is contained in the left
$X$
is contained in the left
![]() ${\mathcal{O}}$
-lattice
${\mathcal{O}}$
-lattice
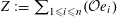 $Z:=\sum _{1\leqslant i\leqslant n}({\mathcal{O}}e_{i})$
, which is the image of
$Z:=\sum _{1\leqslant i\leqslant n}({\mathcal{O}}e_{i})$
, which is the image of
![]() ${\mathcal{O}}^{n}$
under the last isomorphism. Then there exists a sufficiently divisible integer
${\mathcal{O}}^{n}$
under the last isomorphism. Then there exists a sufficiently divisible integer
![]() $r\in \mathbb{Z}_{{\geqslant}1}$
such that
$r\in \mathbb{Z}_{{\geqslant}1}$
such that
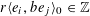 $r\langle e_{i},be_{j}\rangle _{0}\in \mathbb{Z}$
for all
$r\langle e_{i},be_{j}\rangle _{0}\in \mathbb{Z}$
for all
![]() $b\in {\mathcal{O}}$
and
$b\in {\mathcal{O}}$
and
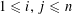 $1\leqslant i,j\leqslant n$
; namely,
$1\leqslant i,j\leqslant n$
; namely,
![]() $r\langle \cdot ,\cdot \rangle _{0}$
induces a positive definite
$r\langle \cdot ,\cdot \rangle _{0}$
induces a positive definite
![]() ${\mathcal{O}}$
-compatible (symmetric) bilinear pairing
${\mathcal{O}}$
-compatible (symmetric) bilinear pairing
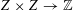 $Z\times Z\rightarrow \mathbb{Z}$
.
$Z\times Z\rightarrow \mathbb{Z}$
.
Let
 $\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2},\ldots ,\unicode[STIX]{x1D700}_{h}$
be a
$\unicode[STIX]{x1D700}_{1},\unicode[STIX]{x1D700}_{2},\ldots ,\unicode[STIX]{x1D700}_{h}$
be a
![]() $\mathbb{Z}$
-basis of
$\mathbb{Z}$
-basis of
![]() ${\mathcal{O}}_{+}$
, and let
${\mathcal{O}}_{+}$
, and let
 $\unicode[STIX]{x1D700}_{h+1},\unicode[STIX]{x1D700}_{h+2},\ldots ,\unicode[STIX]{x1D700}_{m}$
be a
$\unicode[STIX]{x1D700}_{h+1},\unicode[STIX]{x1D700}_{h+2},\ldots ,\unicode[STIX]{x1D700}_{m}$
be a
![]() $\mathbb{Z}$
-basis of
$\mathbb{Z}$
-basis of
![]() ${\mathcal{O}}_{-}$
. Let
${\mathcal{O}}_{-}$
. Let
![]() $\unicode[STIX]{x1D71B}$
be any element of
$\unicode[STIX]{x1D71B}$
be any element of
![]() $K^{\times }$
of positive valuation. Let
$K^{\times }$
of positive valuation. Let
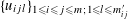 $\{u_{ijl}\}_{1\leqslant i\leqslant j\leqslant m;1\leqslant l\leqslant m_{ij}^{\prime }}$
, where
$\{u_{ijl}\}_{1\leqslant i\leqslant j\leqslant m;1\leqslant l\leqslant m_{ij}^{\prime }}$
, where
![]() $m_{ij}^{\prime }=h$
when
$m_{ij}^{\prime }=h$
when
![]() $i=j$
and
$i=j$
and
![]() $m_{ij}^{\prime }=n$
when
$m_{ij}^{\prime }=n$
when
![]() $i<j$
, be elements in
$i<j$
, be elements in
![]() $\widetilde{R}^{\times }$
that are multiplicatively independent as in Lemma 5.10. Then we define a symmetric bimultiplicative pairing
$\widetilde{R}^{\times }$
that are multiplicatively independent as in Lemma 5.10. Then we define a symmetric bimultiplicative pairing
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{1}:Z\times Z\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{1}:Z\times Z\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
satisfying the compatibility
 $$\begin{eqnarray}\langle bz,w\rangle _{1}=\langle z,b^{\star }w\rangle _{1}\end{eqnarray}$$
$$\begin{eqnarray}\langle bz,w\rangle _{1}=\langle z,b^{\star }w\rangle _{1}\end{eqnarray}$$
for all
 $b\in {\mathcal{O}}_{+}\oplus {\mathcal{O}}_{-}$
and
$b\in {\mathcal{O}}_{+}\oplus {\mathcal{O}}_{-}$
and
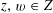 $z,w\in Z$
by setting:
$z,w\in Z$
by setting:
(1)
 $\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{i}\rangle _{1}:=u_{ijl}\cdot \unicode[STIX]{x1D71B}^{r\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{i}\rangle _{0}}$
for all
$\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{i}\rangle _{1}:=u_{ijl}\cdot \unicode[STIX]{x1D71B}^{r\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{i}\rangle _{0}}$
for all
 $1\leqslant i\leqslant n$
and
$1\leqslant i\leqslant n$
and
 $1\leqslant l\leqslant h$
(in which case
$1\leqslant l\leqslant h$
(in which case
 $\unicode[STIX]{x1D700}_{l}^{\star }=\unicode[STIX]{x1D700}_{l}$
is compatible with
$\unicode[STIX]{x1D700}_{l}^{\star }=\unicode[STIX]{x1D700}_{l}$
is compatible with
 $\langle e_{i},\unicode[STIX]{x1D700}_{l}^{\star }e_{i}\rangle _{0}=\langle \unicode[STIX]{x1D700}_{l}^{\star }e_{i},e_{i}\rangle _{0}=\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{i}\rangle _{0}$
);
$\langle e_{i},\unicode[STIX]{x1D700}_{l}^{\star }e_{i}\rangle _{0}=\langle \unicode[STIX]{x1D700}_{l}^{\star }e_{i},e_{i}\rangle _{0}=\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{i}\rangle _{0}$
);(2)
 $\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{i}\rangle _{1}:=1$
for all
$\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{i}\rangle _{1}:=1$
for all
 $1\leqslant i\leqslant n$
and
$1\leqslant i\leqslant n$
and
 $h<l\leqslant m$
(in which case
$h<l\leqslant m$
(in which case
 $\unicode[STIX]{x1D700}_{l}^{\star }=-\unicode[STIX]{x1D700}_{l}$
forces
$\unicode[STIX]{x1D700}_{l}^{\star }=-\unicode[STIX]{x1D700}_{l}$
forces
 $\langle e_{i},\unicode[STIX]{x1D700}_{l}^{\star }e_{i}\rangle _{0}=\langle \unicode[STIX]{x1D700}_{l}^{\star }e_{i},e_{i}\rangle _{0}=\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{i}\rangle _{0}=0$
); and
$\langle e_{i},\unicode[STIX]{x1D700}_{l}^{\star }e_{i}\rangle _{0}=\langle \unicode[STIX]{x1D700}_{l}^{\star }e_{i},e_{i}\rangle _{0}=\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{i}\rangle _{0}=0$
); and(3)
 $\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{j}\rangle _{1}:=u_{ijl}\cdot \unicode[STIX]{x1D71B}^{r\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{j}\rangle _{0}}$
for all
$\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{j}\rangle _{1}:=u_{ijl}\cdot \unicode[STIX]{x1D71B}^{r\langle e_{i},\unicode[STIX]{x1D700}_{l}e_{j}\rangle _{0}}$
for all
 $1\leqslant i<j\leqslant n$
and
$1\leqslant i<j\leqslant n$
and
 $1\leqslant l\leqslant m$
,
$1\leqslant l\leqslant m$
,
and by extending the values of the pairing to the whole domain
![]() $Z\times Z$
by symmetry, bimultiplicativity, and the rule that
$Z\times Z$
by symmetry, bimultiplicativity, and the rule that
 $\langle ae_{i},be_{j}\rangle _{1}:=\langle e_{i},a^{\star }be_{j}\rangle _{1}$
for all
$\langle ae_{i},be_{j}\rangle _{1}:=\langle e_{i},a^{\star }be_{j}\rangle _{1}$
for all
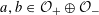 $a,b\in {\mathcal{O}}_{+}\oplus {\mathcal{O}}_{-}$
and
$a,b\in {\mathcal{O}}_{+}\oplus {\mathcal{O}}_{-}$
and
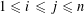 $1\leqslant i\leqslant j\leqslant n$
. Note that this is well defined because
$1\leqslant i\leqslant j\leqslant n$
. Note that this is well defined because
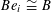 $Be_{i}\cong B$
as left
$Be_{i}\cong B$
as left
![]() $B$
-modules, for all
$B$
-modules, for all
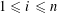 $1\leqslant i\leqslant n$
. Also, note that
$1\leqslant i\leqslant n$
. Also, note that
 $\widetilde{\unicode[STIX]{x1D710}}\circ \langle \cdot ,\cdot \rangle _{1}$
is a positive multiple of
$\widetilde{\unicode[STIX]{x1D710}}\circ \langle \cdot ,\cdot \rangle _{1}$
is a positive multiple of
![]() $\langle \cdot ,\cdot \rangle _{0}$
for every non-trivial discrete valuation
$\langle \cdot ,\cdot \rangle _{0}$
for every non-trivial discrete valuation
 $\widetilde{\unicode[STIX]{x1D710}}:\widetilde{K}^{\times }\rightarrow \mathbb{Z}$
.
$\widetilde{\unicode[STIX]{x1D710}}:\widetilde{K}^{\times }\rightarrow \mathbb{Z}$
.
Next, we define an
![]() ${\mathcal{O}}$
-compatible symmetric bilinear pairing
${\mathcal{O}}$
-compatible symmetric bilinear pairing
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{2}:X\times X\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{2}:X\times X\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
satisfying the Galois equivariance
 $$\begin{eqnarray}\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{2}=\unicode[STIX]{x1D6FE}\langle z,w\rangle _{2}\end{eqnarray}$$
$$\begin{eqnarray}\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{2}=\unicode[STIX]{x1D6FE}\langle z,w\rangle _{2}\end{eqnarray}$$
for all
 $\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
and
$\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)$
and
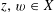 $z,w\in X$
(cf. (5.15)) by setting
$z,w\in X$
(cf. (5.15)) by setting
 $$\begin{eqnarray}\langle z,w\rangle _{2}:=\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}\unicode[STIX]{x1D6FE}^{-1}\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{1}\end{eqnarray}$$
$$\begin{eqnarray}\langle z,w\rangle _{2}:=\mathop{\prod }_{\unicode[STIX]{x1D6FE}\in \operatorname{Gal}(\widetilde{K}/K)}\unicode[STIX]{x1D6FE}^{-1}\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{1}\end{eqnarray}$$
for all
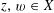 $z,w\in X$
. Note that
$z,w\in X$
. Note that
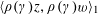 $\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{1}$
are defined for all
$\langle \unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})z,\unicode[STIX]{x1D70C}(\unicode[STIX]{x1D6FE})w\rangle _{1}$
are defined for all
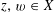 $z,w\in X$
because
$z,w\in X$
because
![]() $X$
is contained in
$X$
is contained in
![]() $Z$
, and that
$Z$
, and that
 $\widetilde{\unicode[STIX]{x1D710}}\circ \langle \cdot ,\cdot \rangle _{2}$
is still positive definite for every non-trivial discrete valuation
$\widetilde{\unicode[STIX]{x1D710}}\circ \langle \cdot ,\cdot \rangle _{2}$
is still positive definite for every non-trivial discrete valuation
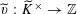 $\widetilde{\unicode[STIX]{x1D710}}:\widetilde{K}^{\times }\rightarrow \mathbb{Z}$
.
$\widetilde{\unicode[STIX]{x1D710}}:\widetilde{K}^{\times }\rightarrow \mathbb{Z}$
.
Finally, we define the desired bimultiplicative pairing
 $$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:Y\times X\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
$$\begin{eqnarray}\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:Y\times X\rightarrow \widetilde{K}^{\times }\end{eqnarray}$$
by setting
 $$\begin{eqnarray}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:=\langle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z),2w\rangle _{2}\end{eqnarray}$$
$$\begin{eqnarray}\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}:=\langle \unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z),2w\rangle _{2}\end{eqnarray}$$
for all
![]() $z\in Y$
and
$z\in Y$
and
![]() $w\in X$
, where
$w\in X$
, where
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
is as in (7.3) (cf. (5.17); but note the coefficient
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
is as in (7.3) (cf. (5.17); but note the coefficient
![]() $2$
of
$2$
of
![]() $w$
). Then
$w$
). Then
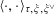 $\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
satisfies the first three conditions (1), (2), and (3) in Proposition 7.7 by the symmetry and positive definiteness of
$\langle \cdot ,\cdot \rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
satisfies the first three conditions (1), (2), and (3) in Proposition 7.7 by the symmetry and positive definiteness of
![]() $\langle \cdot ,\cdot \rangle _{0}$
; by the definitions of the pairings
$\langle \cdot ,\cdot \rangle _{0}$
; by the definitions of the pairings
![]() $\langle \cdot ,\cdot \rangle _{1}$
and
$\langle \cdot ,\cdot \rangle _{1}$
and
![]() $\langle \cdot ,\cdot \rangle _{2}$
; by the choices of
$\langle \cdot ,\cdot \rangle _{2}$
; by the choices of
![]() $\unicode[STIX]{x1D71B}$
(of positive valuation in
$\unicode[STIX]{x1D71B}$
(of positive valuation in
![]() $\widetilde{K}^{\times }$
) and
$\widetilde{K}^{\times }$
) and
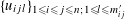 $\{u_{ijl}\}_{1\leqslant i\leqslant j\leqslant n;1\leqslant l\leqslant m_{ij}^{\prime }}$
(of zero valuation in
$\{u_{ijl}\}_{1\leqslant i\leqslant j\leqslant n;1\leqslant l\leqslant m_{ij}^{\prime }}$
(of zero valuation in
![]() $\widetilde{K}^{\times }$
); and by Lemma 7.4 and the relations (7.15) and (7.17). As for the remaining condition (4) in Proposition 7.7, it suffices to note that, since
$\widetilde{K}^{\times }$
); and by Lemma 7.4 and the relations (7.15) and (7.17). As for the remaining condition (4) in Proposition 7.7, it suffices to note that, since
 $2{\mathcal{O}}\subset {\mathcal{O}}_{+}\oplus {\mathcal{O}}_{-}$
, the compatibility (7.14) implies that
$2{\mathcal{O}}\subset {\mathcal{O}}_{+}\oplus {\mathcal{O}}_{-}$
, the compatibility (7.14) implies that
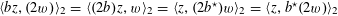 $\langle bz,(2w)\rangle _{2}=\langle (2b)z,w\rangle _{2}=\langle z,(2b^{\star })w\rangle _{2}=\langle z,b^{\star }(2w)\rangle _{2}$
for all
$\langle bz,(2w)\rangle _{2}=\langle (2b)z,w\rangle _{2}=\langle z,(2b^{\star })w\rangle _{2}=\langle z,b^{\star }(2w)\rangle _{2}$
for all
![]() $b\in {\mathcal{O}}$
and
$b\in {\mathcal{O}}$
and
 $z,w\in Z$
.
$z,w\in Z$
.
It remains to show that
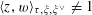 $\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
(as in (7.10)) for all non-zero
$\langle z,w\rangle _{\unicode[STIX]{x1D70F},\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}\neq 1$
(as in (7.10)) for all non-zero
![]() $z\in Y$
and
$z\in Y$
and
![]() $w\in X$
, except when
$w\in X$
, except when
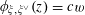 $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)=cw$
for some non-zero
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}(z)=cw$
for some non-zero
![]() $c\in B_{-}$
. Since
$c\in B_{-}$
. Since
![]() $\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
is an embedding, by the defining relation (7.17), it suffices to show that
$\unicode[STIX]{x1D719}_{\unicode[STIX]{x1D709},\unicode[STIX]{x1D709}^{\vee }}$
is an embedding, by the defining relation (7.17), it suffices to show that
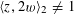 $\langle z,2w\rangle _{2}\neq 1$
for all non-zero
$\langle z,2w\rangle _{2}\neq 1$
for all non-zero
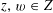 $z,w\in Z$
, except when
$z,w\in Z$
, except when
![]() $z=cw$
for some non-zero
$z=cw$
for some non-zero
![]() $c\in B_{-}$
. By the choice of
$c\in B_{-}$
. By the choice of
 $\{u_{ijl}\}_{1\leqslant i\leqslant j\leqslant n;1\leqslant l\leqslant m_{ij}^{\prime }}$
, the terms in the product (7.16) indexed by different elements
$\{u_{ijl}\}_{1\leqslant i\leqslant j\leqslant n;1\leqslant l\leqslant m_{ij}^{\prime }}$
, the terms in the product (7.16) indexed by different elements
![]() $\unicode[STIX]{x1D6FE}$
have multiplicatively independent values (up to powers of
$\unicode[STIX]{x1D6FE}$
have multiplicatively independent values (up to powers of
![]() $\unicode[STIX]{x1D71B}$
), and so it suffices to show that
$\unicode[STIX]{x1D71B}$
), and so it suffices to show that
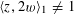 $\langle z,2w\rangle _{1}\neq 1$
for all non-zero
$\langle z,2w\rangle _{1}\neq 1$
for all non-zero
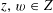 $z,w\in Z$
, except when
$z,w\in Z$
, except when
![]() $z=cw$
for some non-zero
$z=cw$
for some non-zero
![]() $c\in B_{-}$
. Suppose that there are some
$c\in B_{-}$
. Suppose that there are some
 $z=\sum _{1\leqslant i\leqslant n}(a_{i}e_{i})$
and
$z=\sum _{1\leqslant i\leqslant n}(a_{i}e_{i})$
and
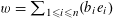 $w=\sum _{1\leqslant i\leqslant n}(b_{i}e_{i})$
in
$w=\sum _{1\leqslant i\leqslant n}(b_{i}e_{i})$
in
![]() $Z$
, where
$Z$
, where
 $(a_{i})_{1\leqslant i\leqslant n}$
and
$(a_{i})_{1\leqslant i\leqslant n}$
and
 $(b_{i})_{1\leqslant i\leqslant n}$
are non-zero
$(b_{i})_{1\leqslant i\leqslant n}$
are non-zero
![]() $n$
-tuples of elements in
$n$
-tuples of elements in
![]() ${\mathcal{O}}$
, such that
${\mathcal{O}}$
, such that
 $\langle z,2w\rangle _{1}=1$
. Then we have
$\langle z,2w\rangle _{1}=1$
. Then we have
 $$\begin{eqnarray}\biggl(\mathop{\prod }_{1\leqslant i\leqslant n}\langle e_{i},2a_{i}^{\star }b_{i}e_{i}\rangle _{1}\biggr)\cdot \biggl(\mathop{\prod }_{1\leqslant i<j\leqslant n}\langle e_{i},2(a_{i}^{\star }b_{j}+b_{i}^{\star }a_{j})e_{j}\rangle _{1}\biggr)=1\end{eqnarray}$$
$$\begin{eqnarray}\biggl(\mathop{\prod }_{1\leqslant i\leqslant n}\langle e_{i},2a_{i}^{\star }b_{i}e_{i}\rangle _{1}\biggr)\cdot \biggl(\mathop{\prod }_{1\leqslant i<j\leqslant n}\langle e_{i},2(a_{i}^{\star }b_{j}+b_{i}^{\star }a_{j})e_{j}\rangle _{1}\biggr)=1\end{eqnarray}$$
in
![]() $\widetilde{K}^{\times }$
(using again the relation
$\widetilde{K}^{\times }$
(using again the relation
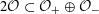 $2{\mathcal{O}}\subset {\mathcal{O}}_{+}\oplus {\mathcal{O}}_{-}$
and the compatibility (7.14)). By pulling out all powers of
$2{\mathcal{O}}\subset {\mathcal{O}}_{+}\oplus {\mathcal{O}}_{-}$
and the compatibility (7.14)). By pulling out all powers of
![]() $\unicode[STIX]{x1D71B}$
, and by the choice of
$\unicode[STIX]{x1D71B}$
, and by the choice of
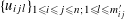 $\{u_{ijl}\}_{1\leqslant i\leqslant j\leqslant n;1\leqslant l\leqslant m_{ij}^{\prime }}$
again, the identity (7.18) is possible only when
$\{u_{ijl}\}_{1\leqslant i\leqslant j\leqslant n;1\leqslant l\leqslant m_{ij}^{\prime }}$
again, the identity (7.18) is possible only when
 $$\begin{eqnarray}a_{i}^{\star }b_{j}+b_{i}^{\star }a_{j}=0\end{eqnarray}$$
$$\begin{eqnarray}a_{i}^{\star }b_{j}+b_{i}^{\star }a_{j}=0\end{eqnarray}$$
in
![]() $B$
, for all
$B$
, for all
 $1\leqslant i\leqslant j\leqslant n$
. Let
$1\leqslant i\leqslant j\leqslant n$
. Let
![]() $i_{0}$
(respectively
$i_{0}$
(respectively
![]() $j_{0}$
) be the smallest index
$j_{0}$
) be the smallest index
![]() $i$
(respectively
$i$
(respectively
![]() $j$
) such that
$j$
) such that
![]() $a_{i}\neq 0$
(respectively
$a_{i}\neq 0$
(respectively
![]() $b_{j}\neq 0$
), which exists by assumption. If
$b_{j}\neq 0$
), which exists by assumption. If
![]() $i_{0}\neq j_{0}$
, then
$i_{0}\neq j_{0}$
, then
 $a_{i_{0}}^{\star }b_{j_{0}}+b_{i_{0}}^{\star }a_{j_{0}}\neq 0$
, which contradicts the condition (7.19). If
$a_{i_{0}}^{\star }b_{j_{0}}+b_{i_{0}}^{\star }a_{j_{0}}\neq 0$
, which contradicts the condition (7.19). If
![]() $i_{0}=j_{0}$
, then the condition (7.19) implies that
$i_{0}=j_{0}$
, then the condition (7.19) implies that
 $$\begin{eqnarray}c:=a_{i_{0}}b_{i_{0}}^{-1}\end{eqnarray}$$
$$\begin{eqnarray}c:=a_{i_{0}}b_{i_{0}}^{-1}\end{eqnarray}$$
is a non-zero element of
![]() $B_{-}$
, because
$B_{-}$
, because
 $$\begin{eqnarray}c^{\star }=(b_{i_{0}}^{\star })^{-1}a_{i_{0}}^{\star }=(b_{i_{0}}^{\star })^{-1}(a_{i_{0}}^{\star }b_{i_{0}})b_{i_{0}}^{-1}=(b_{i_{0}}^{\star })^{-1}(-b_{i_{0}}^{\star }a_{i_{0}})b_{i_{0}}^{-1}=-a_{i_{0}}b_{i_{0}}^{-1}=-c.\end{eqnarray}$$
$$\begin{eqnarray}c^{\star }=(b_{i_{0}}^{\star })^{-1}a_{i_{0}}^{\star }=(b_{i_{0}}^{\star })^{-1}(a_{i_{0}}^{\star }b_{i_{0}})b_{i_{0}}^{-1}=(b_{i_{0}}^{\star })^{-1}(-b_{i_{0}}^{\star }a_{i_{0}})b_{i_{0}}^{-1}=-a_{i_{0}}b_{i_{0}}^{-1}=-c.\end{eqnarray}$$
Moreover, for every
![]() $j\geqslant i_{0}$
, the condition (7.19) implies that
$j\geqslant i_{0}$
, the condition (7.19) implies that
 $$\begin{eqnarray}a_{j}=(b_{i_{0}}^{\star })^{-1}(b_{i_{0}}^{\star }a_{j})=(b_{i_{0}}^{\star })^{-1}(-a_{i_{0}}^{\star }b_{j})=-c^{\star }b_{j}=cb_{j}.\end{eqnarray}$$
$$\begin{eqnarray}a_{j}=(b_{i_{0}}^{\star })^{-1}(b_{i_{0}}^{\star }a_{j})=(b_{i_{0}}^{\star })^{-1}(-a_{i_{0}}^{\star }b_{j})=-c^{\star }b_{j}=cb_{j}.\end{eqnarray}$$
Thus,
![]() $z=cw$
for some non-zero
$z=cw$
for some non-zero
![]() $c\in B_{-}$
, as desired.◻
$c\in B_{-}$
, as desired.◻
Based on the combination of Propositions 7.7, 7.9, and 7.13, the same arguments as before give the following analogues of Theorem 6.1, Corollary 6.2, Theorem 6.4, and Corollary 6.5.
Theorem 7.20. Let
![]() $R$
,
$R$
,
![]() $k$
,
$k$
,
![]() $K$
,
$K$
,
![]() $S$
,
$S$
,
![]() $s$
, and
$s$
, and
![]() $\unicode[STIX]{x1D702}$
be as in the beginning of §4. Let
$\unicode[STIX]{x1D702}$
be as in the beginning of §4. Let
![]() ${\mathcal{O}}$
be as in the beginning of this §7, but assume moreover that
${\mathcal{O}}$
be as in the beginning of this §7, but assume moreover that
 $B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is a division algebra. Given any tori
$B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is a division algebra. Given any tori
![]() $T_{s}$
and
$T_{s}$
and
![]() $T_{s}^{\vee }$
over
$T_{s}^{\vee }$
over
![]() $s$
with character groups
$s$
with character groups
![]() $\text{}\underline{X}_{s}$
and
$\text{}\underline{X}_{s}$
and
![]() $\text{}\underline{Y}_{s}$
, respectively, that are étale sheaves of left
$\text{}\underline{Y}_{s}$
, respectively, that are étale sheaves of left
![]() ${\mathcal{O}}$
-lattices, and an
${\mathcal{O}}$
-lattices, and an
![]() ${\mathcal{O}}$
-equivariant embedding
${\mathcal{O}}$
-equivariant embedding
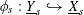 $\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
with finite cokernel, inducing an
$\unicode[STIX]{x1D719}_{s}:\text{}\underline{Y}_{s}{\hookrightarrow}\text{}\underline{X}_{s}$
with finite cokernel, inducing an
![]() ${\mathcal{O}}$
-equivariant isogeny
${\mathcal{O}}$
-equivariant isogeny
 $\unicode[STIX]{x1D706}_{T_{s}}=\unicode[STIX]{x1D719}_{s}^{\ast }:T_{s}\rightarrow T_{s}^{\vee }$
, there exists an object
$\unicode[STIX]{x1D706}_{T_{s}}=\unicode[STIX]{x1D719}_{s}^{\ast }:T_{s}\rightarrow T_{s}^{\vee }$
, there exists an object
![]() $(G,\unicode[STIX]{x1D706},i)$
in
$(G,\unicode[STIX]{x1D706},i)$
in
 $\operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)$
(see Definition 7.1) such that
$\operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)$
(see Definition 7.1) such that
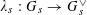 $\unicode[STIX]{x1D706}_{s}:G_{s}\rightarrow G_{s}^{\vee }$
can be identified with
$\unicode[STIX]{x1D706}_{s}:G_{s}\rightarrow G_{s}^{\vee }$
can be identified with
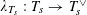 $\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some
$\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some
![]() ${\mathcal{O}}$
-equivariant isomorphisms
${\mathcal{O}}$
-equivariant isomorphisms
![]() $G_{s}\cong T_{s}$
and
$G_{s}\cong T_{s}$
and
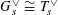 $G_{s}^{\vee }\cong T_{s}^{\vee }$
over
$G_{s}^{\vee }\cong T_{s}^{\vee }$
over
![]() $s$
), and such that
$s$
), and such that
![]() $G_{\unicode[STIX]{x1D702}}$
is absolutely simple except in the two cases (A) and (B) in Proposition 7.9.
$G_{\unicode[STIX]{x1D702}}$
is absolutely simple except in the two cases (A) and (B) in Proposition 7.9.
Corollary 7.21. Let
![]() ${\mathcal{O}}$
be as in Theorem 7.20. Given any field
${\mathcal{O}}$
be as in Theorem 7.20. Given any field
![]() $k$
and any complete discrete valuation ring
$k$
and any complete discrete valuation ring
![]() $R$
with residue field
$R$
with residue field
![]() $k$
, any torus with endomorphisms by
$k$
, any torus with endomorphisms by
![]() ${\mathcal{O}}$
over
${\mathcal{O}}$
over
![]() $k$
can be realized as the special fiber of some semi-abelian scheme over
$k$
can be realized as the special fiber of some semi-abelian scheme over
![]() $R$
whose generic fiber is an abelian variety with endomorphisms by
$R$
whose generic fiber is an abelian variety with endomorphisms by
![]() ${\mathcal{O}}$
over
${\mathcal{O}}$
over
![]() $K$
(which can be principally polarized) that is absolutely simple except in the two cases (A) and (B) in Proposition 7.9.
$K$
(which can be principally polarized) that is absolutely simple except in the two cases (A) and (B) in Proposition 7.9.
Theorem 7.22. Let
![]() ${\mathcal{O}}$
be as in Theorem 7.20. Given any
${\mathcal{O}}$
be as in Theorem 7.20. Given any
![]() $(G,\unicode[STIX]{x1D706},i)$
in
$(G,\unicode[STIX]{x1D706},i)$
in
 $\operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)$
as in Theorem 7.20, there exists some
$\operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R)$
as in Theorem 7.20, there exists some
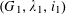 $(G_{1},\unicode[STIX]{x1D706}_{1},i_{1})$
in
$(G_{1},\unicode[STIX]{x1D706}_{1},i_{1})$
in
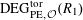 $\operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R_{1})$
(see Remark 7.2) such that
$\operatorname{DEG}_{\text{PE},{\mathcal{O}}}^{\text{tor}}(R_{1})$
(see Remark 7.2) such that
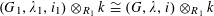 $(G_{1},\unicode[STIX]{x1D706}_{1},i_{1})\otimes _{R_{1}}k\cong (G,\unicode[STIX]{x1D706},i)\otimes _{R_{1}}k$
, and such that the generic fiber
$(G_{1},\unicode[STIX]{x1D706}_{1},i_{1})\otimes _{R_{1}}k\cong (G,\unicode[STIX]{x1D706},i)\otimes _{R_{1}}k$
, and such that the generic fiber
![]() $G_{1,\unicode[STIX]{x1D702}_{1}}$
is absolutely simple except in the two cases (A) and (B) in Proposition 7.9. Consequently, the special fiber
$G_{1,\unicode[STIX]{x1D702}_{1}}$
is absolutely simple except in the two cases (A) and (B) in Proposition 7.9. Consequently, the special fiber
 $\unicode[STIX]{x1D706}_{1,s}:G_{1,s}\rightarrow G_{1,s}^{\vee }$
of
$\unicode[STIX]{x1D706}_{1,s}:G_{1,s}\rightarrow G_{1,s}^{\vee }$
of
![]() $\unicode[STIX]{x1D706}_{1}$
can also be identified with
$\unicode[STIX]{x1D706}_{1}$
can also be identified with
 $\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some
$\unicode[STIX]{x1D706}_{T_{s}}:T_{s}\rightarrow T_{s}^{\vee }$
(via some
![]() ${\mathcal{O}}$
-equivariant isomorphisms
${\mathcal{O}}$
-equivariant isomorphisms
 $G_{1,s}\cong T_{s}$
and
$G_{1,s}\cong T_{s}$
and
 $G_{1,s}^{\vee }\cong T_{s}^{\vee }$
over
$G_{1,s}^{\vee }\cong T_{s}^{\vee }$
over
![]() $s$
).
$s$
).
These assertions remain true with
 $S_{1}=\operatorname{Spec}(R_{1})$
replaced with some connected affine étale neighborhood
$S_{1}=\operatorname{Spec}(R_{1})$
replaced with some connected affine étale neighborhood
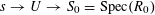 $s\rightarrow U\rightarrow S_{0}=\operatorname{Spec}(R_{0})$
of
$s\rightarrow U\rightarrow S_{0}=\operatorname{Spec}(R_{0})$
of
![]() $s$
.
$s$
.
Corollary 7.23. Let
![]() ${\mathcal{O}}$
be as in Theorem 7.20. Given any field
${\mathcal{O}}$
be as in Theorem 7.20. Given any field
![]() $k$
and any complete discrete valuation ring
$k$
and any complete discrete valuation ring
![]() $R$
with residue field
$R$
with residue field
![]() $k$
, any torus with endomorphisms by
$k$
, any torus with endomorphisms by
![]() ${\mathcal{O}}$
over
${\mathcal{O}}$
over
![]() $k$
can be realized as the special fiber of some semi-abelian scheme over some connected affine étale neighborhood
$k$
can be realized as the special fiber of some semi-abelian scheme over some connected affine étale neighborhood
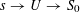 $s\rightarrow U\rightarrow S_{0}$
of
$s\rightarrow U\rightarrow S_{0}$
of
![]() $s$
that is generically an abelian variety with endomorphisms by
$s$
that is generically an abelian variety with endomorphisms by
![]() ${\mathcal{O}}$
(which can be principally polarized) that is absolutely simple except in the two cases (A) and (B) in Proposition 7.9.
${\mathcal{O}}$
(which can be principally polarized) that is absolutely simple except in the two cases (A) and (B) in Proposition 7.9.
By combining Corollaries 7.21 and 7.23, we obtain the following strengthening of our main theorem.
Theorem 7.24. In Theorem 1.3, suppose
![]() $T$
has endomorphisms by
$T$
has endomorphisms by
![]() ${\mathcal{O}}$
, where
${\mathcal{O}}$
, where
![]() ${\mathcal{O}}$
is as in the beginning of this §7, but with the additional assumption that
${\mathcal{O}}$
is as in the beginning of this §7, but with the additional assumption that
 $B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is a division algebra. Then we may assume that the semi-abelian scheme
$B={\mathcal{O}}\otimes _{\mathbb{Z}}\mathbb{Q}$
is a division algebra. Then we may assume that the semi-abelian scheme
![]() $G$
also has endomorphisms by
$G$
also has endomorphisms by
![]() ${\mathcal{O}}$
and, instead of (2) in Theorem 1.3, that
${\mathcal{O}}$
and, instead of (2) in Theorem 1.3, that
![]() $G_{\unicode[STIX]{x1D702}}$
is absolutely simple except in the two cases (A) and (B) in Proposition 7.9.
$G_{\unicode[STIX]{x1D702}}$
is absolutely simple except in the two cases (A) and (B) in Proposition 7.9.
Remark 7.25. Conversely, as mentioned in the introduction, by [Reference Raynaud19, IX, 1.4], [Reference Faltings and Chai7, Ch. I, Proposition 2.7], or [Reference Lan14, Proposition 3.3.1.5], any endomorphism structure on the generic fiber
![]() $G_{\unicode[STIX]{x1D702}}$
necessarily and uniquely extends to the whole semi-abelian scheme
$G_{\unicode[STIX]{x1D702}}$
necessarily and uniquely extends to the whole semi-abelian scheme
![]() $G$
, and also (by reduction) to the torus
$G$
, and also (by reduction) to the torus
![]() $T$
we stared with. Hence, there has been no loss of generality in considering only tori with endomorphisms by the same orders.
$T$
we stared with. Hence, there has been no loss of generality in considering only tori with endomorphisms by the same orders.
Remark 7.26. Certainly, there are many examples of orders
![]() ${\mathcal{O}}$
(with positive involutions) defining endomorphism structures of abelian varieties of certain dimension
${\mathcal{O}}$
(with positive involutions) defining endomorphism structures of abelian varieties of certain dimension
![]() $n$
, but cannot possibly have actions on any
$n$
, but cannot possibly have actions on any
![]() $n$
-dimensional tori. For example, already when
$n$
-dimensional tori. For example, already when
![]() $n=1$
, no CM elliptic curve can degenerate to any one-dimensional torus. In fact, one can generalize this to show that certain abelian varieties must have potential good reductions everywhere: see [Reference Lan11, §4.2] (and the review of the literature there) for a systematic discussion.
$n=1$
, no CM elliptic curve can degenerate to any one-dimensional torus. In fact, one can generalize this to show that certain abelian varieties must have potential good reductions everywhere: see [Reference Lan11, §4.2] (and the review of the literature there) for a systematic discussion.
Remark 7.27. The two exceptional cases (A) and (B) in Proposition 7.9, and therefore also in Theorems 7.20, 7.22, and 7.24, correspond to the two exceptional cases (b) and (d) in [Reference Shimura20, §4, Theorem 5], which are treated in more detail in [Reference Shimura20, §4, Propositions 17 and 18]. These results in [Reference Shimura20, §4] are relevant for our investigation of degenerations of abelian varieties into tori, because the corresponding complex moduli can be non-compact, and because their toroidal compactifications can be compared with the corresponding ones in [Reference Lan14, Theorem 6.4.1.1] in a way that respects the degenerations of abelian varieties into semi-abelian varieties along the boundary, by [Reference Lan12, Theorem 4.1.1 and Proposition 4.2.2]. (More precisely, some subcases of the two exceptional cases (b) and (d) in [Reference Shimura20, §4, Theorem 5] are still irrelevant, because the corresponding complex moduli are compact, and therefore cannot parameterize non-trivial degenerations of abelian varieties, by [Reference Lan11, §4.2]. Similarly, the remaining exceptional cases (a), (c), and (e) in [Reference Shimura20, §4, Theorem 5], which are treated in more detail in [Reference Shimura20, §4, Propositions 14, 15, and 19], are also irrelevant, because the corresponding complex moduli are compact.)
Acknowledgements
We would like to thank the anonymous referees for their helpful comments.