Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-06-27T20:54:23.723Z Has data issue: false hasContentIssue false
  • English
  • Français

Metric monads

Published online by Cambridge University Press:  10 September 2021

Jiří Rosický Open the ORCID record for Jiří Rosický [Opens in a new window]
Jiří Rosický*
Affiliation:
Department of Mathematics and Statistics, Masaryk University, Faculty of Sciences, Kotlářská 2, 611 37 Brno, Czech Republic
*
*Corresponding author. Email: rosicky@math.muni.cz
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We develop universal algebra over an enriched category 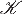and relate it to finitary enriched monads over 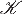. Using it, we deduce recent results about ordered universal algebra where inequations are used instead of equations. Then we apply it to metric universal algebra where quantitative equations are used instead of equations. This contributes to understanding of finitary monads on the category of metric spaces.

Keywords

Equational theorymonadenriched categorymetric spaceposet
Type
Paper
Information
Mathematical Structures in Computer Science , Volume 31 , Issue 5 , May 2021 , pp. 535 - 552
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Footnotes

*

Supported by the Grant Agency of the Czech Republic under the grant 19-00902S

References

Adámek, J., Dostál, M. and Velebil, J. (2011a). A categorical view of varieties of ordered algebras, arXiv:2011.13839.Google Scholar
Adámek, J., Ford, C., Milius, S. and Schröder, L. (2011b). Finitary monads on the category of posets, arXiv:2011.14796.Google Scholar
Adámek, J., Milius, S., Moss, L. S. and Urbat, H. (2015). On finitary functor and their presentations. J. Comp. Syst. Sci. 81 813–833.CrossRefGoogle Scholar
Adámek, J. and Rosický, J. (1994). Locally Presentable and Accessible Categories, Cambridge University Press.CrossRefGoogle Scholar
Adámek, J. and Rosický, J. (1991). What are locally generated categories? In Proc. Categ. Conf. Como 1990. Lecture Notes in Math. 1488, 14–19.Google Scholar
Adámek, J. and Rosický, J. (2006). Approximate injectivity and smallness in metric-enriched categories, arXiv:2006.01399.Google Scholar
Adámek, J., Rosický, J. and Vitale, E. M. (2011). Algebraic Theories, Cambridge University Press.Google Scholar
Bird, G. J. (1984). Limits in 2-categories of locally-presented categories, Sydney Category Seminar Report.Google Scholar
Bloom, S. (1976). Varieties of ordered algebras. J. Comput. System Sci. 13 200–212.CrossRefGoogle Scholar
Borceux, F. (1994). Handbook of Categorical Algebra 2, Cambridge University Press.Google Scholar
Bourke, J. (2010). Codescent objects in 2-dimensional universal algebra, PhD Thesis, University of Sydney.Google Scholar
Bourke, J. and Garner, R. (2019). Monads and theories. Adv. Math. 351 1024–1071.CrossRefGoogle Scholar
Dubuc, E. J. (1970). Enriched semantics-structure (meta) adjointness. Rev. Un. Mat. Argentina 25 5–26.Google Scholar
Di Liberti, I. and Rosický, J. (2009). Enriched locally generated categories, arXiv:2009.10980.Google Scholar
Fritz, T. and Perrone, P. (2019). A probability monad as the colimit of spaces of finite samples. Theory Appl. Categ. 34 170–220.Google Scholar
Gabriel, P. and Ulmer, F. (1971). Lokal präsentierbare Kategorien, Lecture Notes in Math., 221, Springer.Google Scholar
Hino, W. (2016). Varieties of metric and quantitative algebras, arXiv:1612.06054.Google Scholar
Hyland, M. and Power, J. (2007). The category theoretic understanding of universal algebra, Lawvere theories and monads. Electron. Notes Theor. Comput. Sci. 172 437–458.CrossRefGoogle Scholar
Kelly, G. M. (1982a). Basic Concepts of Enriched Category Theory, Cambridge University Press.Google Scholar
Kelly, G. M. (1982b). Structures defined by finite limits in the enriched context I. Cah. Topol. Gém. Différ. Catég. 23 3–42.Google Scholar
Kelly, G. M. and Lack, S. (2001). -CAT is locally presentable or locally bounded if is so. Theory Appl. Categ. 8 555–575.Google Scholar
Lack, S. and Rosický, J. (2011). Notions of Lawvere theory. Appl. Categ. Structures 19 363–391.CrossRefGoogle Scholar
Lawvere, F.W. (2004). Functorial semantics of algebraic theories. Dissertation, Columbia University 1963; Reprints in Theory Appl. Categ. 5 23–107.Google Scholar
Lawvere, F. W. (1973). Metric spaces, generalized logic, and closed categories. Rend. Sem. Mat. Fis. Milano 43 135–166.CrossRefGoogle Scholar
Lieberman, M. and Rosický, J. (2017). Metric abstract elementary classes as accessible categories. J. Symbolic Logic 82 1022–1040.CrossRefGoogle Scholar
Linton, F. E. J. (1966). Some aspects of equational categories. In: Conf. Categ. Algebra (La Jolla 1965), Springer, 84–94.CrossRefGoogle Scholar
Linton, F. E. J. (1969). An Outline of Functorial Semantics. Lect. Notes in Math. 80, Springer, 7–52.CrossRefGoogle Scholar
Lucyshyn-Wright, R. B. B. (2014). Enriched factorization systems. Theory Appl. Categ. 29 475–495.Google Scholar
Lucyshyn-Wright, R. B. B. (2016). Enriched algebraic theories and monads for a system of arities. Theory Appl. Categ. 31 01–137.Google Scholar
Makkai, M. and Paré, R. (1989). Accessible categories: The foundation of Categorical Model Theory. Contemp. Math. 104, AMS.CrossRefGoogle Scholar
Mardare, R., Panangaden, P. and Plotkin, G. (2016). Quantitative algebraic reasoning, In: Proc. LICS 2016, 700–709.CrossRefGoogle Scholar
Mardare, R., Panangaden, P. and Plotkin, G. (2017). On the axiomatizability of quantitative algebras. In: Proc. LICS 2017.Google Scholar
Moggi, E. (1991). Notions of computation and monads. Inf. Comp. 93 55–92.CrossRefGoogle Scholar
Nishizawa, K. and Power, J. (2009). Lawvere theories enriched over a general base. J. Pure Appl. Algebra 213 377–386.CrossRefGoogle Scholar
Plotkin, G. and Power, J. (2004). Computational effects and operations: An overview . Electron. Notes Theor. Comp. Sci. 73 149–163.CrossRefGoogle Scholar
Porst, H.-E. (2008). On categories of monoids, comonoids, and bimonoids. Quest. Math. 31 127–139.CrossRefGoogle Scholar
Power, J. (1999). Enriched Lawvere theories. Theory Appl. Categ. 6 83–93.Google Scholar
Rezk, C. W. (1996). Spaces of algebra structures and cohomology of operads, Thesis MIT.Google Scholar
Rosický, J. (1981). On algebraic categories. In: Coll. Math. Soc. J. Bolyai, 29. (Universal Algebra, Esztergom 1977), Budapest 1981, 662–690.Google Scholar
Rosický, J. (2011). Are Banach spaces monadic?, arXiv:2011.07543, to appear in Comm. Algebra.Google Scholar
Rosický, J. and Tholen, W. (2018). Approximate injectivity. Appl. Categ. Structures 26 699–716.CrossRefGoogle Scholar
Weaver, N. (1995). Quasi-varieties of metric algebras. Algebra Universalis 33 1–9.CrossRefGoogle Scholar