No CrossRef data available.
Article contents
Hom weak ω-categories of a weak ω-category
Published online by Cambridge University Press: 12 May 2022
Abstract
Classical definitions of weak higher-dimensional categories are given inductively, for example, a bicategory has a set of objects and hom categories, and a tricategory has a set of objects and hom bicategories. However, more recent definitions of weak n-categories for all natural numbers n, or of weak
 $\omega$
-categories, take more sophisticated approaches, and the nature of the ‘hom is often not immediate from the definitions’. In this paper, we focus on Leinster’s definition of weak
$\omega$
-categories, take more sophisticated approaches, and the nature of the ‘hom is often not immediate from the definitions’. In this paper, we focus on Leinster’s definition of weak
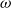 $\omega$
-category based on an earlier definition by Batanin and construct, for each weak
$\omega$
-category based on an earlier definition by Batanin and construct, for each weak
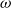 $\omega$
-category
$\omega$
-category
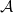 $\mathcal{A}$
, an underlying (weak
$\mathcal{A}$
, an underlying (weak
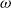 $\omega$
-category)-enriched graph consisting of the same objects and for each pair of objects x and y, a hom weak
$\omega$
-category)-enriched graph consisting of the same objects and for each pair of objects x and y, a hom weak
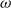 $\omega$
-category
$\omega$
-category
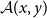 $\mathcal{A}(x,y)$
. We also show that our construction is functorial with respect to weak
$\mathcal{A}(x,y)$
. We also show that our construction is functorial with respect to weak
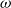 $\omega$
-functors introduced by Garner.
$\omega$
-functors introduced by Garner.
Keywords
- Type
- Special Issue: The Power Festschrift
- Information
- Mathematical Structures in Computer Science , Volume 32 , Special Issue 4: The Power Festschrift , April 2022 , pp. 420 - 441
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
Footnotes
We gratefully acknowledge the support of Royal Society grant IE160402. The second author is supported by ERATO HASUO Metamathematics for Systems Design Project (No. JPMJER1603), JST. No data were generated in association with this paper.





