Hostname: page-component-848d4c4894-4hhp2 Total loading time: 0 Render date: 2024-04-30T16:40:06.346Z Has data issue: false hasContentIssue false
  • English
  • Français

An approximation algorithm for the 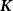$\boldsymbol{K}$-prize-collecting multicut problem in trees with submodular penalties

Published online by Cambridge University Press:  17 April 2024

Xiaofei Liu Open the ORCID record for Xiaofei Liu [Opens in a new window]  and
Weidong Li
Xiaofei Liu
Affiliation:
School of Information Science and Engineering, Yunnan University, Kunming, 650500, China
Weidong Li*
Affiliation:
School of Mathematics and Statistics, Yunnan University, Kunming, 650500, China
*
Corresponding author: Weidong Li; Email: weidongmath@126.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 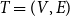$T=(V,E)$ be a tree in which each edge is assigned a cost; let 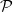$\mathcal{P}$ be a set of source–sink pairs of vertices in V in which each source–sink pair produces a profit. Given a lower bound K for the profit, the K-prize-collecting multicut problem in trees with submodular penalties is to determine a partial multicut 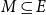$M\subseteq E$ such that the total profit of the disconnected pairs after removing M from T is at least K, and the total cost of edges in M plus the penalty of the set of still-connected pairs is minimized, where the penalty is determined by a nondecreasing submodular function. Based on the primal-dual scheme, we present a combinatorial polynomial-time algorithm by carefully increasing the penalty. In the theoretical analysis, we prove that the approximation factor of the proposed algorithm is 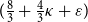$(\frac{8}{3}+\frac{4}{3}\kappa+\varepsilon)$, where $\kappa$ is the total curvature of the submodular function and $\varepsilon$ is any fixed positive number. Experiments reveal that the objective value of the solutions generated by the proposed algorithm is less than 130% compared with that of the optimal value in most cases.

Keywords

Multicut problem in trees with submodular penaltiesK prize collectingapproximation algorithmprimal-dual scheme
Type
Special Issue: TAMC 2022
Information
Mathematical Structures in Computer Science , First View , pp. 1 - 18
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

a

A preliminary version of this paper appeared in the Proceedings of the 17th Annual Conference on Theory and Applications of Models of Computation, pp. 262–271, 2022.

References

Bentz, C. and Le Bodic, P. (2020). Complexity of the multicut problem, in its vanilla, partial and generalized versions, in graphs of bounded treewidth. Theoretical Computer Science 809 239–249.CrossRefGoogle Scholar
Chawla, S., Krauthgamer, R., Kumar, R., Rabani, Y. and Sivakumar, D. (2006). On the hardness of approximating multicut and sparsest-cut. Computational Complexity 15 94–114.CrossRefGoogle Scholar
Conforti, M. and Cornuéjols, G. (1984). Submodular set functions, matroids and the greedy algorithm: Tight worst-case bounds and some generalizations of the rado-edmonds theorem. Discrete Applied Mathematics 7 (3) 251–274.CrossRefGoogle Scholar
Costa, M.-C., Létocart, L. and Roupin, F. (2005). Minimal multicut and maximal integer multiflow: A survey. European Journal of Operational Research 162 (1) 55–69.CrossRefGoogle Scholar
Dahlhaus, E., Johnson, D. S., Papadimitriou, C. H., Seymour, P. D. and Yannakakis, M. (1994). The complexity of multiterminal cuts. SIAM Journal on Computing 23 (4) 864–894.CrossRefGoogle Scholar
Fujishige, S. (2005). Submodular Functions and Optimization (2nd edn). Elsevier.Google Scholar
Garg, N., Vazirani, V. V. and Yannakakis, M. (1996). Approximate max-flow min-(multi)cut theorems and their applications. SIAM Journal on Computing 25 235–251.CrossRefGoogle Scholar
Garg, N., Vazirani, V. V. and Yannakakis, M. (1997). Primal-dual approximation algorithms for integral flow and multicut in trees. Algorithmica 18 (1) 3–20.CrossRefGoogle Scholar
Golovin, D., Nagarajan, V. and Singh, M. (2006). Approximating the k-multicut problem. In: 2006 ACM-SIAM Symposium on Discrete Algorithms (SODA 2006). SIAM, 621–630.CrossRefGoogle Scholar
Guo, J., Liu, W. and Hou, B. (2023). An approximation algorithm for P-prize-collecting set cover problem. Journal of the Operations Research Society of China 11 207–217.Google Scholar
Hu, T. C. (1963). Multi-commodity network flows. Operations Research 11 344–360.CrossRefGoogle Scholar
Hou, X., Liu, W. and Hou, B. (2020). An approximation algorithm for the k-prize-collecting multicut on a tree problem. Theoretical Computer Science 844 26–33.CrossRefGoogle Scholar
Keuper, M., Andres, B. and & Brox, T. (2015). Motion trajectory segmentation via minimum cost multicuts. In: 2015 IEEE International Conference on Computer Vision (ICCV 2015), IEEE, 3271–3279.CrossRefGoogle Scholar
Khot, S. and Regev, O. (2008). Vertex cover might be hard to approximate to with $2-\varepsilon$ . Journal of Computer and System Sciences 74 (3) 335–349.CrossRefGoogle Scholar
Könemann, J., Parekh, O. and Segev, D. (2011). A unified approach to approximating partial covering problems. Algorithmica 59 (4) 489–509.CrossRefGoogle Scholar
Levin, A. and Segev, D. (2006). Partial multicuts in trees. Theoretical Computer Science 369 384–395.CrossRefGoogle Scholar
Li, Y., Du, D., Xiu, N. and Xu, D. (2015). Improved approximation algorithms for the facility location problems with linear/submodular penalties. Algorithmica 73 (2) 460–482.CrossRefGoogle Scholar
Liu, X. and Li, W. (2022). Combinatorial approximation algorithms for the submodular multicut problem in trees with submodular penalties. Journal of Combinatorial Optimization 44 1964–1976.CrossRefGoogle Scholar
Liu, X. and Li, W. (2023). The B-prize-collecting multicut problem in paths, spider graphs and rings. International Journal of Foundations of Computer Science 2023 1–14.Google Scholar
Liu, X., Li, W. & Yang, J. (2022). A primal-dual approximation algorithm for the k-prize-collecting minimum vertex cover problem with submodular penalties. Frontiers of Computer Science 17 173404.CrossRefGoogle Scholar
Mestre, J. (2008). Lagrangian relaxation and partial cover problem. In: 2008 International Symposium on Theoretical Aspects of Computer Science (STACS 2008), LIPIcs, 539–550.Google Scholar
Orlin, J. B. (2009). A faster strongly polynomial time algorithm for submodular function minimization. Mathematical Programming 118 237–251.Google Scholar
Pedrosa, L. L. C. and Rosado, H. K. K. (2022). A 2-approximation for the k-prize-collecting steiner tree problem. Algorithmica 84 3522–3558.CrossRefGoogle Scholar
Ren, C., Xu, D., Du, D. and Li, M. (2022). An improved primal-dual approximation algorithm for the k-means problem with penalties. Mathematical Structures in Computer Science 32 151–163.CrossRefGoogle Scholar
Tang, S., Andriluka, M., Andres, B. and Schiele, B. (2017). Multiple people tracking by lifted multicut and person re-identification. In: 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2017), IEEE, 3701–3710.CrossRefGoogle Scholar
Xu, D., Wang, F., Du, D. and Wu, C. (2016). Approximation algorithms for submodular vertex cover problems with linear/submodular penalties using primal-dual technique. Theoretical Computer Science 630 117–125.CrossRefGoogle Scholar
Yang, R., Xu, D., Cheng, Y., Gao, C. and Du, D.-Z. (2019). Streaming submodular maximization under noises. In: 39th IEEE International Conference on Distributed Computing Systems (ICDCS 2019), IEEE, 348–357.CrossRefGoogle Scholar
Yannakakis, M., Kanellakis, P. C., Cosmadakis, S. S. and Papadimitriou, C. H. (1983). Cutting and partitioning a graph after a fixed pattern. In: 1983 International Colloquium on Automata, Languages and Programming (ICALP 1983), Springer, 712–722.CrossRefGoogle Scholar
Zhang, P. (2022). The LP-rounding plus greed approach for partial optimization revisited. Frontiers of Computer Science 16 (1) 161402.CrossRefGoogle Scholar
Zhang, P., Zhu, D. and Luan, J. (2012). An approximation algorithm for the generalized k-multicut problem. Discrete Applied Mathematics 160 (7–8) 1240–1247.CrossRefGoogle Scholar