Article contents
Not every countable complete distributive lattice is sober
Published online by Cambridge University Press: 28 July 2023
Abstract
The study of the sobriety of Scott spaces has got a relatively long history in domain theory. Lawson and Hoffmann independently proved that the Scott space of every continuous directed complete poset (usually called domain) is sober. Johnstone constructed the first directed complete poset whose Scott space is non-sober. Soon after, Isbell gave a complete lattice with a non-sober Scott space. Based on Isbell’s example, Xu, Xi, and Zhao showed that there is even a complete Heyting algebra whose Scott space is non-sober. Achim Jung then asked whether every countable complete lattice has a sober Scott space. The main aim of this paper is to answer Jung’s problem by constructing a countable complete lattice whose Scott space is non-sober. This lattice is then modified to obtain a countable distributive complete lattice with a non-sober Scott space. In addition, we prove that the topology of the product space 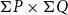 $\Sigma P\times \Sigma Q$ coincides with the Scott topology of the product poset
$\Sigma P\times \Sigma Q$ coincides with the Scott topology of the product poset 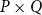 $P\times Q$ if the set Id(P) and Id(Q) of all incremental ideals of posets P and Q are both countable. Based on this, it is deduced that a directed complete poset P has a sober Scott space, if Id(P) is countable and
$P\times Q$ if the set Id(P) and Id(Q) of all incremental ideals of posets P and Q are both countable. Based on this, it is deduced that a directed complete poset P has a sober Scott space, if Id(P) is countable and 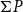 $\Sigma P$ is coherent and well filtered. In particular, every complete lattice L with Id(L) countable has a sober Scott space.
$\Sigma P$ is coherent and well filtered. In particular, every complete lattice L with Id(L) countable has a sober Scott space.
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press
References
- 1
- Cited by





