No CrossRef data available.
Article contents
Hofmann-Mislove type definitions of non-Hausdorff spaces
Published online by Cambridge University Press: 27 June 2022
Abstract
One of the most important results in domain theory is the Hofmann-Mislove Theorem, which reveals a very distinct characterization for the sober spaces via open filters. In this paper, we extend this result to the d-spaces and well-filtered spaces. We do this by introducing the notions of Hofmann-Mislove-system (HM-system for short) and 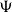 $\Psi$
-well-filtered space, which provide a new unified approach to sober spaces, well-filtered spaces, and d-spaces. In addition, a characterization for
$\Psi$
-well-filtered space, which provide a new unified approach to sober spaces, well-filtered spaces, and d-spaces. In addition, a characterization for 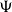 $\Psi$
-well-filtered spaces is provided via
$\Psi$
-well-filtered spaces is provided via 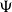 $\Psi$
-sets. We also discuss the relationship between
$\Psi$
-sets. We also discuss the relationship between 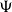 $\Psi$
-well-filtered spaces and H-sober spaces considered by Xu. We show that the category of complete
$\Psi$
-well-filtered spaces and H-sober spaces considered by Xu. We show that the category of complete 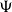 $\Psi$
-well-filtered spaces is a full reflective subcategory of the category of
$\Psi$
-well-filtered spaces is a full reflective subcategory of the category of 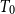 $T_0$
spaces with continuous mappings. For each HM-system
$T_0$
spaces with continuous mappings. For each HM-system 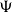 $\Psi$
that has a designated property, we show that a
$\Psi$
that has a designated property, we show that a 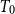 $T_0$
space X is
$T_0$
space X is 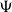 $\Psi$
-well-filtered if and only if its Smyth power space
$\Psi$
-well-filtered if and only if its Smyth power space 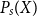 $P_s(X)$
is
$P_s(X)$
is 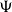 $\Psi$
-well-filtered.
$\Psi$
-well-filtered.
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
Footnotes
This research was supported by the National Natural Science Foundation of China (Nos. 1210010153, 12071199, 12071188, 11661057, 11871097), Jiangsu Provincial Department of Education (21KJB110008) and the Natural Science Foundation of Jiangxi Province, China (No. 20192ACBL20045).





