Hostname: page-component-7479d7b7d-jwnkl Total loading time: 0 Render date: 2024-07-11T23:23:21.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Unsound ordinals

Published online by Cambridge University Press:  24 October 2008

A. R. D. Mathias
A. R. D. Mathias
Affiliation:
Peterhouse, Cambridge
Get access Rights & Permissions [Opens in a new window]

Abstract

An ordinal is termed unsound if it has subsets An (nεω) such that un-countably many ordinals are realised as order types of sets of the form ∪ {An|nε a} where a ⊆ ω. It is shown that if ω1 is regular and 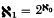then the least unsound ordinal is exactly but that if ω1 is regular and 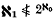the least unsound ordinal, assuming one exists, is at least 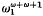. Arguments due to Kechris and Woodin are presented showing that under the axiom of determinacy there is an unsound ordinal less than ω2. The relation between unsound ordinals and ideals on w is explored. The paper closes with a list of open problems.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 96 , Issue 3 , November 1984 , pp. 391 - 411
Copyright
Copyright © Cambridge Philosophical Society 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Bachmann, H.. Transfinite Zahlen. Ergeb. Math. Grenzgeb. Neue Folge, Heft 1 (Springer-Verlag, 1955).Google Scholar
[2]Cabal Seminar 76–77. Lecture Notes in Math. vol. 689, ed. Kechris, A. S. and Moschovakis, Y. N. (Springer-Verlag, 1978).CrossRefGoogle Scholar
[3]Cabal Seminar 77–79. Lecture Notes in Math. vol. 839, ed. Kechris, A. S., Martin, D. A. and Moschovakis, Y. N. (Springer-Verlag, 1981).CrossRefGoogle Scholar
[4]Cabal Seminar 79–81. Lecture Notes in Math. vol. 1019, ed. Kechris, A. S., Martinand, D. A.Moschovakis, Y. N. (Springer-Verlag, 1983).CrossRefGoogle Scholar
[5]Guaspari, D.. Trees, Norms and Scales, Surveys in Set Theory, ed. Mathias, A. R. D.. London Math. Soc. Lecture Note Ser. 87 (Cambridge University Press, 1983).Google Scholar
[6]Jalali-Naini, S.-A.. The monotone subsets of Cantor Space, niters and descriptive set theory. D.Phil, thesis, Oxford, 1976.Google Scholar
[7]Jech, T. J.. The Axiom of Choice. Studies in Logic, vol. 75 (North Holland, 1973).Google Scholar
[8]R, A.. Mathias, D.. A remark on rare filters. Colloq. Math. Soc. Janos Bolyai, 10. Infinite and Finite Sets, to Paul Erdös on his 60th birthday, ed. Hajnal, A., Rado, R. and Sós, V. T. (North Holland, 1975), 1095–1097.Google Scholar
[9]Milner, E. C. and Rado, R.. The pigeon-hole principle for ordinal numbers. Proc. London Math. Soc. (3), 15 (1965), 750–768.CrossRefGoogle Scholar
[10]Moschovakis, Y. N.. Descriptive Set Theory. Studies in Logic, vol. 100 (North Holland Publishing Company, 1980).Google Scholar
[11]Shelah, S., unpublished.Google Scholar
[12]Sierpiński, W.. Cardinal and Ordinal Numbers. Monograf. Mat. Tom 34 (Warsaw, 1958).Google Scholar
[13]Toulmin, G. H.. Shuffling ordinals and transfinite dimension. Proc. London Math. Soc. (3), 4 (1954), 177–195.CrossRefGoogle Scholar