Hostname: page-component-76fb5796d-25wd4 Total loading time: 0 Render date: 2024-04-28T15:49:52.531Z Has data issue: false hasContentIssue false
  • English
  • Français

Stable cohomotopy and cobordism of abelian groups

Published online by Cambridge University Press:  24 October 2008

C. T. Stretch
C. T. Stretch
Affiliation:
Mathematical Institute, University of Oxford
Get access Rights & Permissions [Opens in a new window]

Extract

The object of this paper is to prove that for a finite abelian group G the natural map 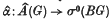is injective, where Â(G) is the completion of the Burnside ring of G and σ0(BG) is the stable cohomotopy of the classifying space BG of G. The map â is detected by means of an M U* exponential characteristic class for permutation representations constructed in (11). The result is a generalization of a theorem of Laitinen (4) which treats elementary abelian groups using ordinary cohomology. One interesting feature of the present proof is that it makes explicit use of the universality of the formal group law of M U*. It also involves a computation of M U*(BG) in terms of the formal group law. This may be of independent interest. Since writing the paper the author has discovered that M U*(BG) has previously been calculated by Land-weber(5).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 90 , Issue 2 , September 1981 , pp. 273 - 278
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Tom Dieck, D.Steenrod-Operationen in Kobordismen-Theorien. Math. Z. 107 (1968), 380–401.Google Scholar
(2)Gunawardena, J. H. Segal's conjecture for cyclic groups of odd prime order. J. T. Knight prize essay, Cambridge, 1980.Google Scholar
(3)Hazewinkel, M.Formal groups and applications (Academic Press, New York, San Francisco, London, 1978).Google Scholar
(4)Laitinen, E. On the Burnside ring and stable cohomotopy of a finite group. Aarhus University preprint no. 14, 1977/8.Google Scholar
(5)Landweber, P. S.Coherence, flatness and cobordism of classifying spaces. Proc. Adv. Study Institute on Algebraic Topology, Aarhus (1970), 256–269.Google Scholar
(6)Lin, W. H.On conjectures of Mahowald, Segal and Sullivan. Math. Proc. Camb. Philos. Soc. 87 (1980), 456–469.Google Scholar
(7)Lin, W. H., Davis, D. M., Mahowald, M. E. and Adams, J. F.Calculations of Lin's Ext groups. Math. Proc. Camb. Philos. Soc. 87 (1980), 459–469.Google Scholar
(8)Priddy, S. B.On Ω∞S∞ and the infinite symmetric group. Proc. Symp. Pure Math. Amer. Math. Soc. 22 (1971), 217–220.Google Scholar
(9)Ravenel, D. C.The Segal conjecture for cyclic groups. Butt. London Math. Soc. 13 (1981), 42–44.Google Scholar
(10)Segal, G. B.Categories and cohomology theories. Topology 13 (1974), 293–312.Google Scholar
(11)Segal, G. B. and Stretch, C. T.Characteristic classes for permutation representations. Math. Proc. Camb. Philos. Soc. 90 (1981), 265–272.Google Scholar
(12)Serre, J. P. Algèbre locale - multiplicités. Lecture Notes in Mathematics vol. 11 (Springer-Verlag, Berlin and New York, 1975).Google Scholar
(13)Quillen, D.Elementary proofs of some results of cobordism theory using Steenrod operations. Advances in Math. 7 (1971), 29–56.CrossRefGoogle Scholar
(14)Quillen, D.On the formal group laws of unoriented and complex cobordism theory. Bull. Amer. Math. Soc. 75 (1969), 1293–98.Google Scholar