Article contents
Redei reciprocity, governing fields and negative Pell
Published online by Cambridge University Press: 19 April 2021
Abstract
We discuss the origin, an improved definition and the key reciprocity property of the trilinear symbol introduced by Rédei [16] in the study of 8-ranks of narrow class groups of quadratic number fields. It can be used to show that such 8-ranks are ‘governed’ by Frobenius conditions on the primes dividing the discriminant, a fact used in the recent work of A. Smith [18, 19]. In addition, we explain its impact in the progress towards proving my conjectural density for solvability of the negative Pell equation 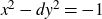 $x^2-dy^2=-1$
.
$x^2-dy^2=-1$
.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 172 , Issue 3 , May 2022 , pp. 627 - 654
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
References
- 3
- Cited by




