We study projectional properties of Poisson cut-out sets E in non-Euclidean spaces. In the first Heisenbeg group 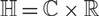\[\mathbb{H} = \mathbb{C} \times \mathbb{R}\], endowed with the Korányi metric, we show that the Hausdorff dimension of the vertical projection 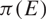\[\pi (E)\] (projection along the center of 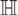\[\mathbb{H}\]) almost surely equals 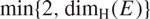\[\min \{ 2,{\dim _\operatorname{H} }(E)\} \] and that 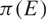\[\pi (E)\] has non-empty interior if 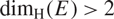\[{\dim _{\text{H}}}(E) > 2\]. As a corollary, this allows us to determine the Hausdorff dimension of E with respect to the Euclidean metric in terms of its Heisenberg Hausdorff dimension 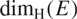\[{\dim _{\text{H}}}(E)\].

We also study projections in the one-point compactification of the Heisenberg group, that is, the 3-sphere 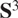\[{{\text{S}}^3}\] endowed with the visual metric d obtained by identifying 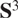\[{{\text{S}}^3}\] with the boundary of the complex hyperbolic plane. In 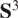\[{{\text{S}}^3}\], we prove a projection result that holds simultaneously for all radial projections (projections along so called “chains”). This shows that the Poisson cut-outs in 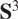\[{{\text{S}}^3}\] satisfy a strong version of the Marstrand’s projection theorem, without any exceptional directions.